洛谷P3209

平面图判断与汉密尔顿回路

最新推荐文章于 2023-03-19 18:20:29 发布

原创最新推荐文章于 2023-03-19 18:20:29 发布 · 312 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#题解

洛谷专栏收录该内容

75 篇文章

订阅专栏

这篇博客介绍了如何判断一个包含汉密尔顿回路的无向图是否为平面图。通过玄学定理确定条件，使用哈密尔顿回路转化为多边形，再利用种类并查集来维护边的相交关系。博客提供了具体的思路和代码实现，并建议读者理解图的结构和相交判断逻辑。

题意简述

给定一个无向图，保证包含一个汉密尔顿回路（给定这个回路，就不用您找了）。判断这个图是不是平面图（画在平面上没有边相交的图）。多组数据。

数据

输入：
2//两组数据
6 9
1 4
1 5
1 6
2 4
2 5
2 6
3 4
3 5
3 6
1 4 2 5 3 6//到此第一组

5 5
1 2
2 3
3 4
4 5
5 1
1 2 3 4 5//到此第二组
输出：
NO
YES

思路

首先根据玄学定理，m要<= $3 n - 6$ 才能有解（如果不满足直接输出NO），这样m就和n在一个数量级了。

接着我们发现一个哈密尔顿回路珂以直接看成一个多边形，先把回路上的边标记掉，后面就不管了。对于一个其他的边，它珂以连在里面，也珂以连在外面。那个更优呢？
~~（爆搜）~~
如果有一个数据结构能够快速的维护边与边之间的香♂蕉&不香♂蕉的关系，那什么都好办了。这是什么呢？？
~~孔子云~~:种类并查集。（不知道的去自学。。。）
然后我们枚举边i和j，如果i和j在回路上一定是没问题的，不会相交。只有回路外的边是需要考虑的。我们用种类并查集维护，空间开 $2 m$ ， $i + m$ 和 $i$ 是对立关系，是一定要相交的。也就是说，如果 $i$ 和 $i + m$ 在同一个集合，就是矛盾的，也就不是平面图。
对于一对边，我们珂以通过其在回路上的位置判断是否相交（具体见下面的图和解释）。当然，如果并查集上显示它们在一个集合（即不会相交），那就矛盾了，直接输出 $N O$ ，返回。否则我们就记录一下 $i, j$ 的相交关系。（合并 $i, j + m$ ，合并 $i + m, j$ ）。

对了，为了方便计算一定会相交的关系（即在回路上是错开的），我们强制把输入的回路上的点换成 $1,2,3,4⋯n1,2,3,4\cdots n$ ，具体实现就是写个id数组做映射，然后把输入篡改掉（改成映射后的点编号）。
（什么你要图？~~自己在学校桌子上画~~好吧我帮你画：）

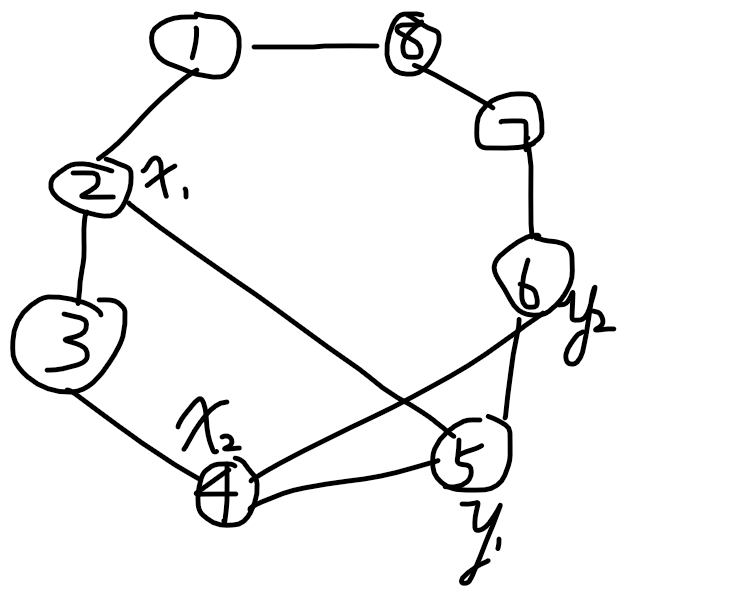
(这个图是代码中判断的第一种"错开"，结合代码好好理解)

代码：

#include<bits/stdc++.h>
#define N 1001000
using namespace std;

class DSU//并查集
{
    private:
        int Father[N];
    public:
        int Cnt[N];
        void Init()
        {
            for(int i=0;i<N;i++)
            {
                Father[i]=i;
                Cnt[i]=1;
            }
        }
        int Find(int x)
        {
            return x==Father[x]?x:Father[x]=Find(Father[x]);
        }
        void Merge(int x,int y)
        {
            int ax=Find(x),ay=Find(y);
            if (Cnt[ax]<Cnt[ay])
            {
                Cnt[ay]+=Cnt[ax];
                Father[ax]=ay;
            }
            else
            {
                Cnt[ax]+=Cnt[ay];
                Father[ay]=ax;
            }
        }
}D;

int id[N];//映射，强行转成1~n
int u[N],v[N],vis[N];//每条边的起点，终点，是否在回路上

int n,m;

void _Init()
{
    memset(id,0,sizeof(id));
    memset(u,0,sizeof(u));
    memset(v,0,sizeof(v));
    memset(vis,0,sizeof(vis));
    D.Init();
}

void _Input()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u[i],&v[i]);
    }
    for(int i=1;i<=n;i++)
    {
        int t;scanf("%d",&t);
        id[t]=i;//强人锁♂男的转换
    }
}

bool cross(int x1,int x2,int y1,int y2)//判断从x1~y1的边和从x1~y2的边是否会交♂叉
{
    if (x1==x2 or y1==y2 or x1==y2 or x2==y1)
    {
        return false;
    }
    if (x1<x2 and y1<y2 and x2<y1) return true;//情况1(已给图)
    if (x2<x1 and y2<y1 and x1<x2) return true;//情况2(自己画)
    return false;
}
void _Solve()
{
    if (m>3*n-6)//特判
    {
        printf("NO\n");
        return;
    }
    for(int i=1;i<=m;i++)
    {
        int x=id[u[i]],y=id[v[i]];
        u[i]=x,v[i]=y;//强制转换
        if (u[i]>v[i]) u[i]^=v[i]^=u[i]^=v[i];//刚刚忘了说了，这边要记得把设u[i]<=v[i]，否则会有问题
    }

    memset(vis,0,sizeof(vis));//多组数据，一定要初始化
    //(我王境泽就是死这，从这里跳下去，也不会是因为我的问题爆0！一定是lg评测姬有bug!)
    //(哎~我忘了初始化~)
    for(int i=1;i<=m;i++)
    {
        vis[i]=(u[i]%n+1/*n和1也相邻，所以要取模*/==v[i]);
    }

    for(int i=1;i<=m;i++)
    {
        if (!vis[i])
        {
            for(int j=1;j<=m;j++)
            {
                if (!vis[j] and cross(u[i],u[j],v[i],v[j]))
                {
                    if (D.Find(i)==D.Find(j))//矛盾的情况
                    {
                        puts("NO");
                        return;
                    }
                    else//不矛盾
                    {
                    	D.Merge(i,j+m);
                    	D.Merge(i+m,j);
                    }
                }
            }
        }
    }
    puts("YES");
}

main()
{
    int T;scanf("%d",&T);
    while(T-->0)
    {
        _Init();
        _Input();
        _Solve();
    }
    return 0;
}