数据结构与算法——优先队列类的C++实现(二叉堆)

优先队列简介：

操作系统表明上看着是支持多个应用程序同时运行，事实上是每个时刻只能有一个进程运行，操作系统会调度不同的进程去运行。每个进程都只能运行一个固定的时间，当超过了该时间，操作系统就会暂停当前运行的进程，去调度其它进程来执行。

实现这种进程调度的一种方法是使用队列。开始的时候进程被放在队列的末尾，调度程序将反复提取队列中的第一个进程来执行，直到运行完毕或时间片用完，若进程没有运行完毕则将该进程放入队列的末尾。这种策略不是特别合适，因为可能一些短的进程需要等待很长的时间才能轮流到。一般来说，运行时间短的进程需要尽快的结束。所以那些运行时间短的进程需要比较高的优先权，同样，那些比较重要的进程也需要比较高的优先权。
这种特殊的应用需要一种特殊的队列-----优先队列。可以用二叉堆实现优先队列。

二叉堆简介：

二叉堆与二叉查找树类似，二叉树有两个性质：结构性质和堆序性质。

结构性质：

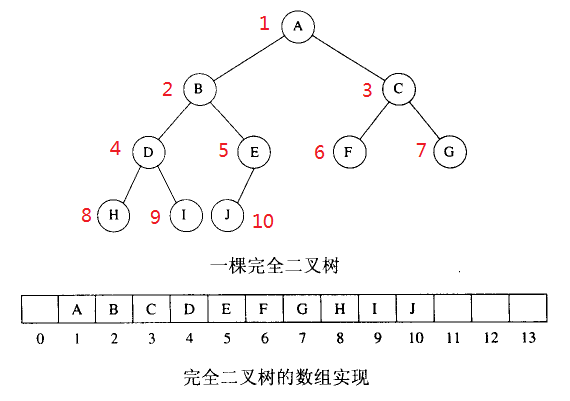
二叉堆是一棵完全二叉树，除了子节点外的其它节点都有两个儿子节点。
一棵高为h的完全二叉树有2^h到2^(h+1) - 1个节点。完全二叉树的高为log(N)，N为节点数目。
由于完全二叉树的特点，实现起来很简单，用简单的数组就可以实现。对于数组中的任意位置i上的元素，其左儿子在位置2*i上，右儿子在(2*i)+1上，其父节点在i/2上（让根节点在位置1）；

下面是一棵完全二叉树的数组实现图示：

堆序性质：

因为如果想快速找到最小单元，则最小单元应该在根上。在堆中，对于每一个节点x,x的值大于等于子节点（叶子节点除外）；没有二叉查找树的要求严格。

二叉堆的数据结构实现：

用一个数组 vector<Comparable> v;来存储所有的元素。
用currentSize来记录当前元素的数目。

vector<Comparable> array;//存储二叉堆的节点 
int currentSize;//当前二叉堆中的节点数目

二叉堆的主要成员函数：

bool isEmpty() const;//判断二叉堆是否为空
const Comparable & findMin() const;//查找最小元素

void insert(const Comparable & x);//插入元素x
void deleteMin();//删除最小元素
void deleteMin(Comparable & minItem);//删除最小元素，并以引用的方式返回该最小元素
void makeEmpty();//清空该二叉堆 
void print() const;//打印该堆元素

void buildHeap();//将元素移动到合适的位置
void percolateDown(int hole);//下移动

二叉堆的主要成员函数介绍：

1、插入insert()：

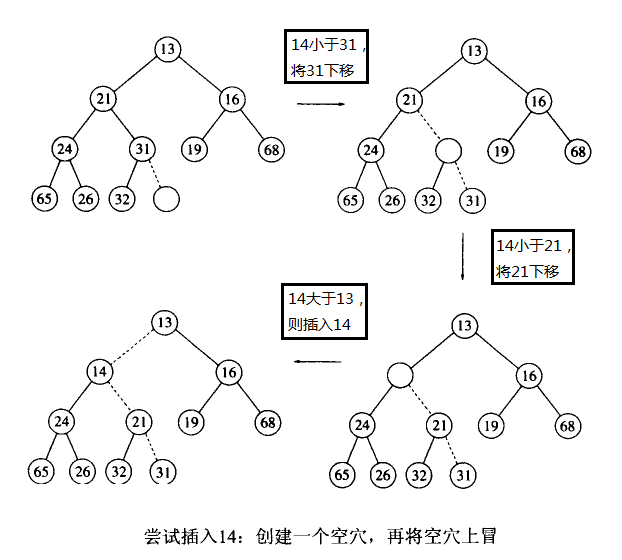
比如：当插入14的时候，第一步在堆的下一个可用的位置建立空穴，如果在该空穴插入14后满足堆序性，则插入成功。
但当在该空穴插入14之后不满足堆序性，则将该空穴的父节点移入空穴，之前的父节点的位置变为了空穴。
然后再尝试插入该新的空穴，如果不满足堆序，则重复之前的操作。

/****************************************************************
*   函数名称：insert(const Comparable & x)
*   功能描述: 删除最小元素
*   参数列表: 无
*   返回结果࿱