一、引言
简单的说,树状数组是线段树的简化形式。
基于这种理解,在拿到一个长度为 9 9 9 的数组以后,十分自然得直接采用向下取整的办法,将长度为 9 9 9 的数组分割为长度分别为 4 4 4 和 5 5 5 的左右两个子区间。再反复进行上面的操作,直到区间长度无法再分。然后依据每层的区间关系,就可以得到一颗二叉树,而这棵二叉树正是区间树(如左图所示)。有了区间树以后,再去掉不必要的区间就获得了最后的树状数组。
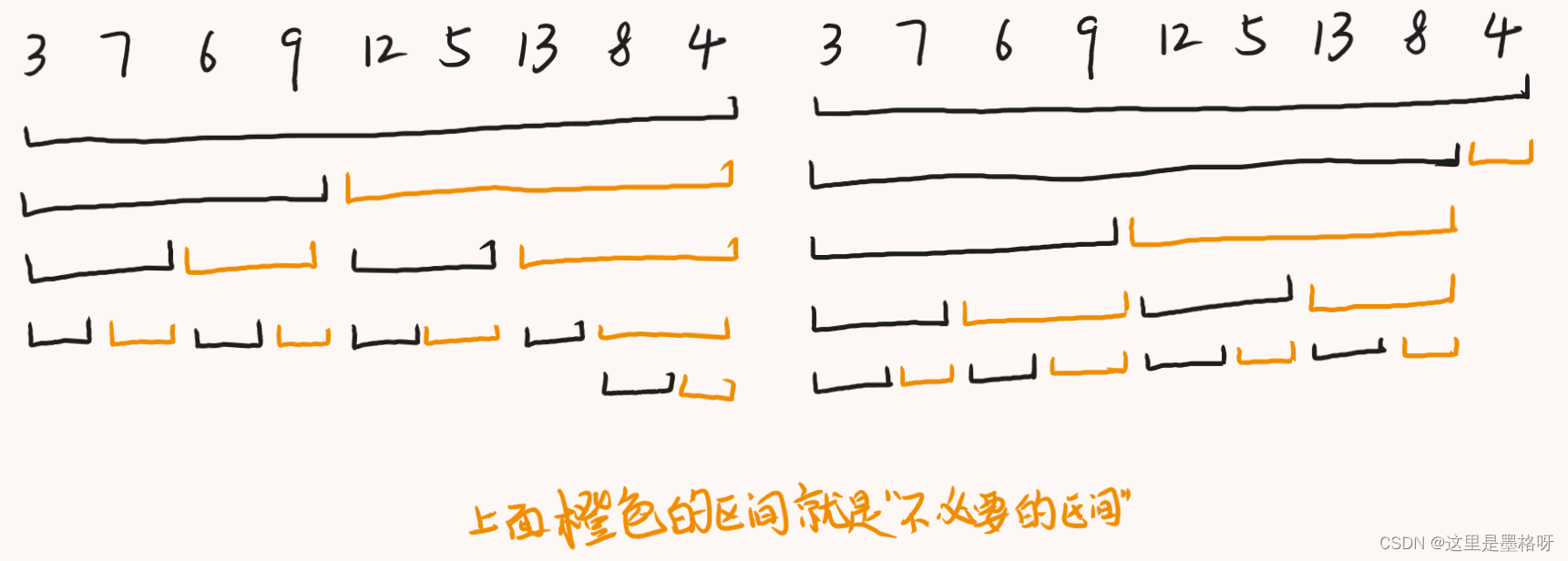
但是实际上,构建树状数组时通常不会采用这种分割方法,而用一种“补”的思想——将数组的长度补充为
2
2
2 的整数次方,然后再进行划分(如右图所示,其中未画出“补”的部分)。与此同时,引入了 lowbit 函数,以求出当前节点的父、子节点的索引号。
观察整个树状数组的推理过程,这种变化是十分突然的,数组长度为什么一定要补成
2
2
2 的整数次方?为什么 lowbit 函数能够建立起节点索引号与区间长度之间的关系?
为了进一步讨论这个问题,我首先做出了一个大胆的猜想,不使用 lowbit 函数能否实现树状数组?
二、一个猜想:“非常规”树状数组
当我们抛弃 lowbit 函数后,要面对的最大的问题就是,程序该如何寻找当前节点的父、子节点?一个可能的解决方案是将目标节点的父、子节点的索引号直接记录下来。于是可以设计下面这个类:
class Node{
public:
int value;
int parent;
int child;
Node(): value(-1), parent(-1), child(-1){}
};
当我们能够寻找到目标节点的父子索引号以后,求区间和、单点修改等操作就与平常的树状数组的操作基本相同了。所以,这个“非常规数组”的关键在于如何 built 操作如何进行?
这时候,我们就要用上第一小节中所说的“树状数组是线段树的简化”的结论了。我们通过仿照线段树的构建过程,我们可以用一个递归算法构建整个树状数组。
三、 2 2 2 的整数次方
区间长度定理
在构建非常规树状数组的时候,存在一种十分蹩脚的情况——奇数长度的数组。因为奇数没有办法被 2 2 2 整除,所以在向下二分的时候,总是要进行一定的取整操作。这就导致程序没有办法均匀地二分数组,总存在一些偏差。而当数组的长度为 2 2 2 的整数次方时,就不存在这种情况。更加有趣的是,这种数组二分建树后的任意一个区间都是 2 2 2 的整数次方!
我们定义第 1 1 1 层只有 1 1 1 个根区间,这是对原数组不进行任何二分操作的结果。第 2 2 2 层是对根区间进行一次二分后的结果,从左往右依次是第 1 1 1 个、第 2 2 2 个区间。接下来的层次都反复进行上面的操作,直到区间不可再分。最终就能够获得一棵树状数组。
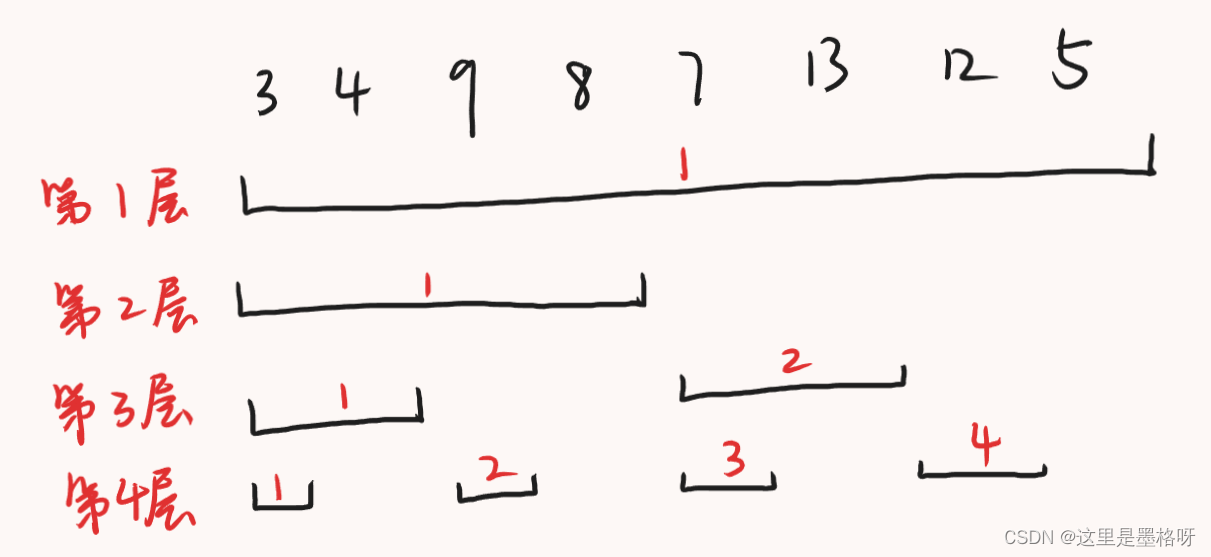
根据前面的推理,很容易发现,当数组的长度是 2 2 2 的整数次方时,每一层区间的长度都是相等的。又因为第一层的区间长度等于原数组的长度,所以,我们可以很容易得到任意层区间的长度。
区间长度定理:
已知数组长度 l = 2 n ( n ∈ Z ∗ ) l=2^n (n \in Z^*) l=2n(n∈Z∗) ,那么将该数组进行二分建树以后,第 h h h 层的区间长度满足如下关系:
l h = { l h − 1 2 1 < h ≤ n 2 n h = 1 l_h = \begin{cases} \frac{l_{h-1}}{2} &1 \lt h\le n \\ 2^n &h = 1 \end{cases} lh={2lh−12n1<h≤nh=1
父子索引号定理
所以,当数组的长度是 2 2 2 的整数次方时,折半建树时就不存在向下取整的问题,子区间的长度一定是相等的。更精确的说,子区间的长度同样是 2 2 2 的整数次方!而这也就意味着,当前节点的父节点的位置,正好是当前索引号加上区间长度!而子节点,就是减去区间长度。
区间长度定理告诉我们一个重要的事实,那就是当前节点的区间长度,父节点
父子索引号定理:
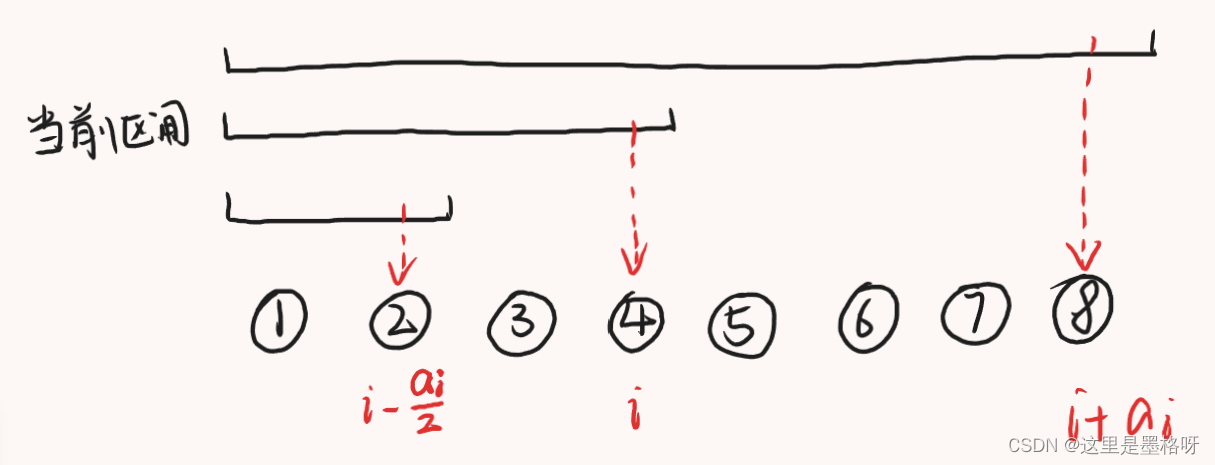
已知数组的长度 l = 2 n ( n ∈ Z ∗ ) l=2^n (n \in Z^*) l=2n(n∈Z∗) ,当前节点的父、子节点的索引号 i p a r e n t i_{parent} iparent 与 i c h i l d i_{child} ichild ,与当前节点的索引号 i i i 有关。具体关系如下:
i p a r e n t = i + l i i c h i l d = i − l i 2 \begin{matrix} i_{parent} = i + l_i \\ i_{child} = i - \frac{l_i}{2} \end{matrix} iparent=i+liichild=i−2li
其中 l i l_i li 代表当前节点的区间长度。
对于这种特殊长度的数组,当前节点的父节点和子节点的位置与区间长度有关!
既然当数组的长度为 2 2 2 的整数次方时有如此有用的性质,那么我们能不能利用起来呢?答案是可以的!我们可以把原数组长度扩充为 2 2 2 的整数次方,多出来的空间用 0 0 0 来填充,如此一来不就可以利用之前的规律了吗?接下来就只剩下一个问题,我们该如何得到当前位置所代表区间的长度?
四、从区间长度到比特位
让我们暂时忘记树状数组,观察一个我们再熟悉不过的问题:
已知一个数组,那么从第 i i i 个元素到第 j j j 个元素之间有多少个元素呢?
解决这个问题十分简单,我们有下面的长度公式:
l
=
j
−
i
+
1
l = j - i + 1
l=j−i+1
观察上面的公式,会有一个很平常,但是很重要的现象,那就是,元素的索引号居然和区间的长度有关系!当然,因为上面的这个公式我们早已司空见惯,但是如果放到树状数组中呢?元素的索引号是不是也和区间的长度有关系?
例如,如果我们要求出红色区间的长度,我们应该这样计算:
【假装有一张图图上画着一个长度为8的树状数组】
把红色的两个数组相减就可以了。很自然的,我们就得到了区间的长度。我们进一步思考相减的更加内在的含义。
前面说到,子区间的长度也是2的整数次方,所以,我们可以分别标注出每个区间的长度:
【假装这里有一张图】
这时候,我们可以很轻易的计算出红色区间的索引号:由三个蓝色区间的长度相加得到。
l
=
2
2
+
2
1
+
2
0
l = 2^2+2^1+2^0
l=22+21+20
上面这个区间长度的计算方法就是lowbit函数发挥作用的关键。如果我们从二进制的角度观察上面的计算,会惊奇发现,每个加数都正好是二进制里的“十”。
100+010+001
而最后一个“1”恰恰是当前区间的长度!那么我们该怎么得到这个所谓的“最后一个
1
1
1 ”呢?lowbit 就恰恰可以做到这件事情!!!
这就是 lowbit 发挥作用的根本原因。
已知一个数组的长度 l = 2 n ( n ∈ Z ∗ ) l = 2^n(n \in Z^*) l=2n(n∈Z∗),对该数组二分建树后,第 h h h 层、第 k k k 个区间的索引号为
f ( h , k ) = c k ⋅ l h = ( 2 k − 1 ) ⋅ 2 n − h + 1 f(h, k) = c_k \cdot l_h = (2k-1) \cdot 2^{n-h+1} f(h,k)=ck⋅lh=(2k−1)⋅2n−h+1
其中,
- c k = 2 k − 1 c_k=2k-1 ck=2k−1 ,表示第 k k k 个区间前面有多少个前置区间;
- l h = 2 n − h + 1 l_h = 2^{n-h+1} lh=2n−h+1,表示第 h h h 层的区间长度;
- 数组索引号从 1 1 1 开始。
五、lowbit
有了上面的讨论,关于树状数组,我们应该就有一个更加深刻的认识了。在树状数组中,表面上看,lowbit函数发挥着重要的作用。更重要的是,如何得到当前节点的父节点和子节点。理论上讲,我们可以通过存储父节点和子节点索引号的方法,绕过lowbit函数。但是,经过巧妙的设计后,lowbit函数可以以更加简单,讨巧的方式解决了前面的问题。这就是树状数组的中lowbit函数的关键。





















 1421
1421











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








