数据结构-算法的空间复杂度（1.2）

目录

1.空间复杂度

1.1 例子

1.2 空间的特殊性质

写在最后：

---

1.空间复杂度

空间复杂度也是一个数学表达式，

是对一个算法在运行过程中临时占用存储空间大小的量度。

他也是用大O渐进表示法。

1.1 例子

例1：

冒泡排序：

void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

这个是开辟了常数个的空间，

（创建变量就是开辟空间）

它创建了几个变量，所以是开辟了常数个的空间，

所以他的空间复杂度是O(1)。

例2：

斐波那契数列：

long long* Fibonacci(size_t n)
{
	if (n == 0)
		return NULL;
	long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}

这里用malloc开辟了n个以上的空间，

所以它的空间复杂度是O(N)。

例3：

阶乘递归：

long long Fac(size_t N)
{
	if (N == 0)
		return 1;
	return Fac(N - 1) * N;
}

这段代码，

因为函数递归，建立函数栈帧，

而函数栈帧里有常数个（空间）变量开辟，

而这段代码，建立了N+1个函数栈帧，

所以它的空间复杂度是O(N)。

1.2 空间的特殊性质

例4：

long long Fib(int N)
{
	if (N < 3)
		return 1;
	return Fib(N - 1) + Fib(N - 2);
}

这段代码的时间复杂度是O(2的N次方)。

但是，它的空间复杂度呢？

实际上，他的空间复杂度是O(N)，而不是O(2的N次方)。

为什么呢？

因为函数递归的过程中会建立栈帧，而这段代码在进行递归的时候，

并不会一直递归到最后才返回，

当它递归到一定程度是，会有函数提前返回，

导致栈帧销毁，当新的栈帧建立的时候，

空间就会被重复使用，

例：

#include <stdio.h>

void f1()
{
	int b = 0;
	printf("%p\n", &b);
}

void f2()
{
	int a = 0;
	printf("%p\n", &a);
}

int main()
{
	f1();
	f2();
	return 0;
}

输出：

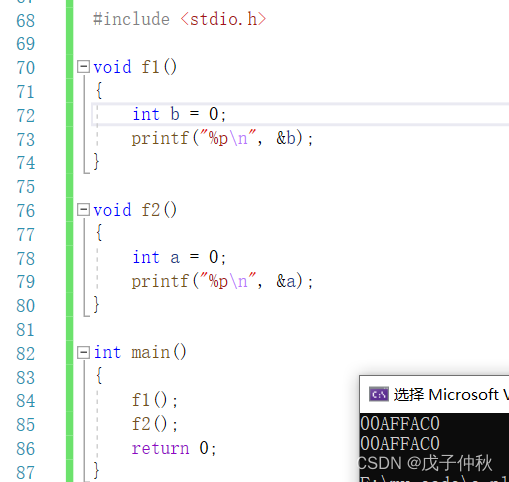
 我们发现，当f1函数的栈帧销毁后，

f2函数栈帧建立，创建的变量地址与f1中创建的变量地址相同，

这就是空间重复利用的特性。

例：

#include <stdio.h>

void f1()
{
	int b = 0;
	printf("%p\n", &b);
}

void f2()
{
	int a = 0;
	printf("%p\n", &a);
	f1();
}

int main()
{
	f2();
	return 0;
}

输出：

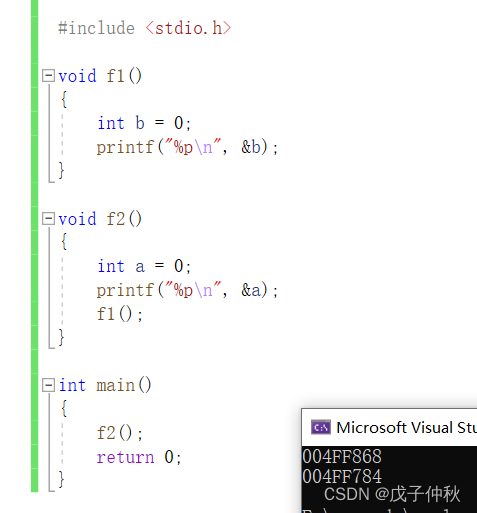
 当f1函数的栈帧没有销毁，

f2函数的变量自然用不了f1函数的空间，

所以他们的地址当然不同了。

写在最后：

以上就是本篇文章的内容了，感谢你的阅读。

如果喜欢本文的话，欢迎点赞和评论，写下你的见解。

如果想和我一起学习编程，不妨点个关注，我们一起学习，一同成长。

之后我还会输出更多高质量内容，欢迎收看。