深入理解C++中的堆：从基本概念到实际应用

一、什么是堆？

堆是一种具有树形结构的数据结构，它遵循堆属性，即：每个节点必须小于其每个子节点。

“堆”这个名字可能来自于这样一个事实：如果堆放一堆东西并希望它能保持平衡，人类更愿意把大的东西放在底部，小的东西放在顶部：

请注意，这与包含动态分配对象的内存区域中的堆完全无关（与栈相对，栈也是一种数据结构的名称）。

堆的一个最重要的特性是，其最小元素位于其根部，易于访问。

在堆中，每个节点理论上可以有任意数量的子节点。但在STL中，堆的节点有两个子节点，因此在本文中将用堆来指代二叉堆。

二、最大堆

堆属性，即每个节点必须小于其子节点，可以推广到另一个比“小于”更通用的比较，如operator<。可以使用对于堆中的数据类型更有意义的某种关系。例如，集合的堆可以使用词典顺序关系。

也可以在堆属性中使用关系“大于”（仍然可以通过反转堆属性并确保子节点小于其父节点来使用operator<来实现）。

这样的堆称为最大堆，这是STL所具有的堆的类型。因此，在本文中，堆指的是二叉最大堆。

在最大堆中，最大的元素位于根部。下面是一个堆的示例：

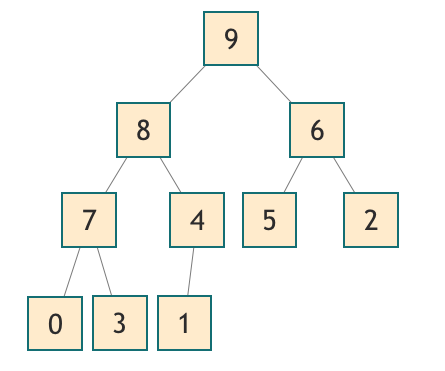
可以看到每个节点都小于其父节点，而最大的节点（9）位于根部。

三、实现堆

要表示诸如堆之类的二叉树，一种实现方法是为每个节点进行动态分配，其中2个指针指向其子节点。

但是有一个更高效（更优雅）的实现方法：将它表示为数组的形式，通过对堆进行层次遍历来实现。即数组从根节点开始，然后是该根节点的子节点，然后是这些子节点的所有子节点，然后是这些子节点的所有子节点。等等…。

这样，最大元素位于数组的第一个位置。

这就是STL表示堆的方式：堆可以存储在std::vector中，例如，元素像上面那样排列在一起。

与为每个节点指向对方的节点相比，此表示方法更有效的原因有几个：

• 只有一个动态分配用于整个堆，而不是每个节点都有一个动态分配；
• 没有指向子节点的指针，因此不需要为它们分配空间；
• 结构的连续布局使其更加友好地缓存。

这一切都很好，但好像不能再遍历树的节点了，因为没有指向子节点（或父节点）的指针。事实上，将二叉树表示为数组的一个好处是，要获取某个索引i处节点的左子节点，只需跳到索引（i + 1）* 2 - 1即可到达左子节点，而右子节点的索引是(i + 1) * 2。


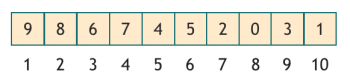
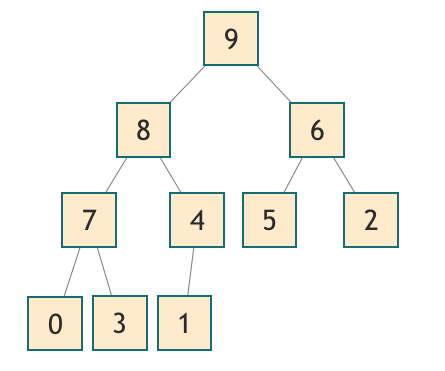
看看堆如何表示为数组，索引从1开始：将其与其初始树状表示进行比较。注意到位置i的节点的两个子节点分别位于位置i * 2和i * 2 + 1吗？当索引从1开始时，这是正确的。

但由于在std::vector中，索引从0开始，因此节点在索引位置的左子节点位于以下位置：

size_t leftChild(size_t index)
{
    return (index + 1) * 2 - 1;
}

节点在索引位置的右子节点的位置为：

size_t rightChild(size_t index)
{
    return (index + 1) * 2;
}

三、使用STL创建和检查堆

现在已经清楚了堆作为数组的表示，接下来看看STL提供的一些算法，这些算法用于在数组内操作堆。

3.1、使用std::make_heap创建堆

首先，使用STL中的std::make_heap算法来构建堆。

如果有一系列可相互比较的对象，可以使用std::make_heap将这个范围重新排列成一个最大堆。示例代码：

std::vector<int> numbers = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};

std::make_heap(begin(numbers), end(numbers));

for (int number : numbers)
{
    std::cout << number << ' ';
}

这段代码输出了重新排列后的数字序列：

9 8 6 7 4 5 2 0 3 1

看起来熟悉吗？这就是作为数组实现的堆！

3.2、检查堆属性

接下来，可以使用std::is_heap来检查给定的集合是否以数组的形式实现了最大堆。

std::is_heap(begin(numbers), end(numbers))

如果集合是最大堆，则返回true，否则返回false。例如，在调用std::make_heap之前，对于前面的示例，它会返回false，在之后会返回true。

有可能集合的开始部分结构化为堆。在这种情况下，std::is_heap_until将返回指向不满足堆属性的集合的第一个位置的迭代器。

auto heapUntil = std::is_heap_until(begin(numbers), end(numbers))

例如，如果集合是堆，std::is_heap_until返回集合的结束。如果第一个元素小于第二个元素，它将返回自堆属性从一开始就被破坏以来的第一个位置。

四、总结

通过本文的阅读，可以系统地了解了C++中堆的基础知识及其在STL中的应用。从堆的概念和最大堆的特性开始，深入探讨了堆的实现方式，介绍了将堆表示为数组的方法，并解释了这种表示方法的优势。随后，介绍了使用STL中的std::make_heap算法来创建堆的方法，以及使用std::is_heap和std::is_heap_until算法来检查堆属性的方式。通过具体的示例代码和图示，读者可以更直观地理解堆的构建和检查过程。