排序算法(1)：简单选择排序

基本思想

  简单选择排序是一种简单并且非常直观的排序算法。它的思想是每次从未排序序列中找到最小值，然后将其放到已排序序列的末尾，重复这一过程直到不存在未排序元素。

算法流程

以长度为 $n$ 的数组为例：

1. 第一趟排序：从第一个元素开始遍历整个数组，找出最小值，和第一个元素交换；
2. 第二趟排序：找出第二个元素到第 $n$ 个元素中的最小值，和第二个元素交换；
3. 第三趟排序：找出第三个元素到第 $n$ 个元素中的最小值，和第三个元素交换；
   ……
4. 第 $n-1$ 趟排序：将第 $n$-1 和第 $n$ 个元素正确排序，排序完成。

演示

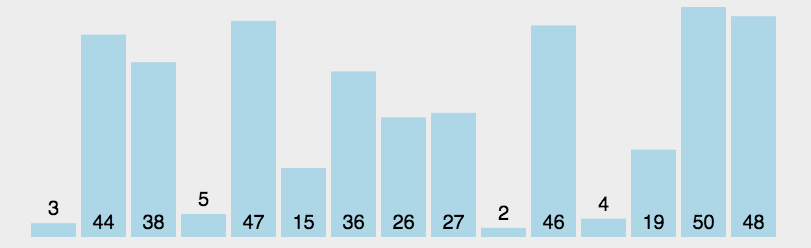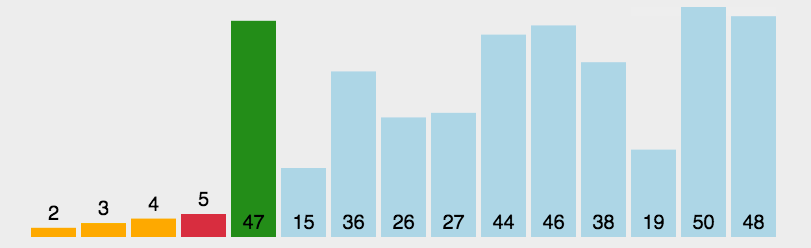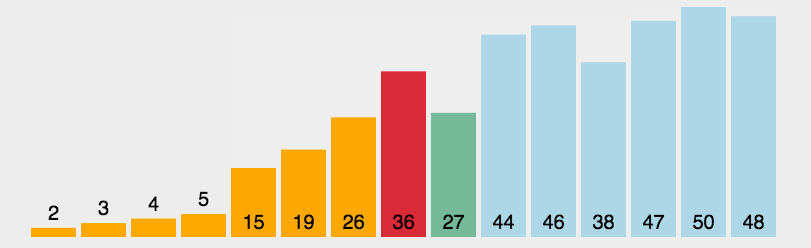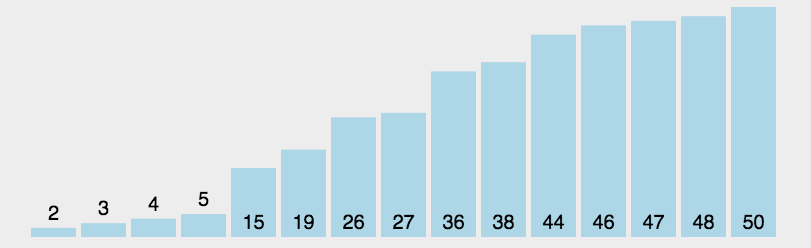
代码实现

简单选择排序 Java 版本的实现如下(代码只给出了排序函数的实现):

public static void selection_sort(int[]  arr){
   // 数组为空或者长度为1不需要排序
     if(arr == null || arr.length < 2){
         return;
     }
     for(int i = 0; i < arr.length - 1; i++){
         int min = i;  // 记录最小值的索引
         for(int j = i + 1; j < arr.length; j++){
             if(arr[j] < arr[min]){
                 min = j;
             }
         }
         // 交换当前值和最小值
         int temp = arr[i];
         arr[i] = arr[min];
         arr[min] = temp;
     }
}

复杂度

• 时间复杂度

  最好情况下：初始数组就是有序的，此时简单选择排序需要进行 $n(n-1)/2$ 次比较，不需要交换元素，时间复杂度为 $O(n^2)$;
  最差情况下：初始数组是倒序的(例如需要从小到大排序但初始数组是从大到小排列的)，此时简单选择排序大约需要进行 $n(n-1)/2$ 次比较和 $n-1$ 次交换，时间复杂度也是$O(n^2)$;
  因此，简单选择排序需要进行的比较次数与初始元素排列情况无关，其平均时间复杂度为$O(n^2)$，最好的情况时间复杂度为$O(n^2)$，最坏情况时间复杂度为$O(n^2)$。

• 空间复杂度：简单选择排序仅需要在交换元素的时候使用额外的常数空间，因此空间复杂度为$O(1)$。

稳定性

  简单选择排序是一种不稳定的排序算法。例如对{2，4，2，1}进行排序，第一轮比较的时候第一个 “2” 会和 “1” 交换位置，破坏原有的两个 “2” 的顺序，因此它是不稳定的。

参考

1. 一文搞定十大排序算法
2. 《算法(第四版)》