昨天下午在书上看到了KMP算法,看了很多很多很多遍都搞不懂什么逻辑和原理;今天上午又听了学长讲了一遍感觉没大听懂,自己又上网找了很多相关文章,试了很多例子,终于找出来KMP算法中手工计算next、next value数组的方法了。下面我借助网上的相关资料结合用我自己的思路说明一下。
一、什么是前缀后缀? 以字符串s"ababcabc"为例:
"a"的前缀和后缀都为空集,共有元素的长度为0;
"ab"的前缀为[a],后缀为[b],共有元素的长度为0;
"aba"的前缀为[a, ab],后缀为[ba, a],共有元素是【a】,长度为1;
"abab"的前缀为[a, ab, aba],后缀为[bab, ab, b],共有元素是【ab】长度为2;
"ababc"的前缀为[a, ab,aba, abab],后缀为[babc,abc, bc, c],共有元素长度为0;
"ababca"的前缀为[a, ab,aba, abab,ababc],后缀为[babca,abca,bca, ca, a],共有元素是【a】,长度为1;
"ababcab"的前缀为[a, ab,aba, abab,ababc,ababca],后缀为[babcab,abcab,bcab,cab, ab, b],共有元素是【ab】,长度为2;
"ababcabc"的前缀为[a, ab,aba, abab,ababc,ababca,ababcab],后缀为[babcabc,abcabc,bcabc,cabc, abc, bc,c],共有元素的长度为0。
二、计算next数组
把上面的共有长度按顺序写下来:
将“共有长度”全部整体向后移一位,首项为定值-1,得到next数组:
三、计算next_value数组
过程如下(next_value简记为nv):
首先nv[0]=-1,是一个定值;
s[1]!=s[0],nv[1]=n[1]=0;
s[2]==s[0],nv[2]=nv[0]=-1;
s[3]==s[1],nv[3]=nv[1]=0;
s[4]!=s[2],nv[4]=n[4]=2;
s[5]==s[2],nv[5]=nv[2]=-1;
s[6]==s[3],nv[6]=nv[3]=0;
s[7]==s[4],nv[7]=nv[4]=2;
你们能找出规律吗?
先将第二项与首项比较:若相同,nv值与首项相同;若不同,nv值等于n值。
如果前一次比较结果:若相同,与下一个字符进行比较;若不同,重复比较得出结果;
若比较结果是相同的情况:赋值的nv的下标依次递加。
可能我表述的不太好,具体请看我上面的步骤,规律是显而易见的。
综上,就得到下面这张表:










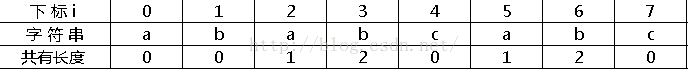
















 1376
1376

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








