转：用一个例子说明Floyd算法

弗洛伊德算法（Floyd's algorithm）是一种用于求带权图中最短路径的算法，适用于带有正负权边的图（但不能有负环）。这种算法也有时被称为弗洛伊德-沃尔什算法。该算法基于动态规划，其时间复杂度为O（V^3），其中V是图中的顶点数。此外，该算法还可用于检测图中的负环并求出传递闭包。

下面是一个使用弗洛伊德算法求图中所有顶点对之间最短路径的示例:

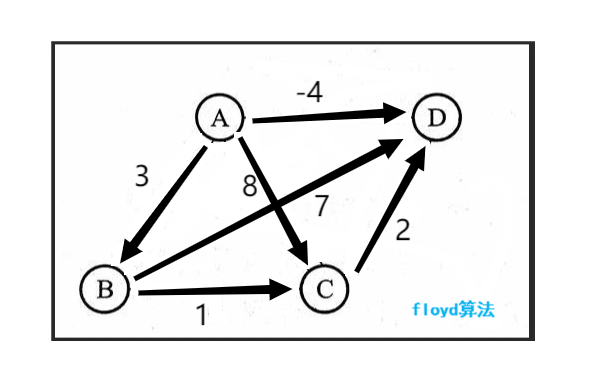
假设我们有一个具有4个顶点（A，B，C和D）的图，以及以下带权边：

　　A -> B: 3

　　A -> C: 8

　　A -> D: -4

　　B -> C: 1

　　B -> D: 7

　　C -> D: 2

我们可以用矩阵表示每对顶点之间的距离，其中第i行第j列的元素表示从顶点i到顶点j的最短距离。最初，我们将矩阵设置为图中边的值：

　　| 0 3 8 -4 |

　　| INF 0 1 7 |

　　| INF INF 0 2 |

　　| INF INF INF 0 |

然后我们使用弗洛伊德算法来更新矩阵:

对于 k = 1 到 V (V 是顶点数)，其中V = 4:

1. 对于 i = 1 到 V:
2. 对于 j = 1 到 V:
3. 如果 dist[i][j] > dist[i][k] + dist[k][j]，则更新 dist[i][j] = dist[i][k] + dist[k][j]

算法运行后，最终矩阵将是:

　　| 0 3 4 0 |

　　| INF 0 1 7 |

　　| INF INF 0 2 |

　　| INF INF INF 0 |

从这个矩阵中，我们可以看出从顶点A到顶点B的最短距离是3，从A到C是4，从A到D是0，从B到C是1等。