DBMS Implementation 笔记 04: Indexing

Indexing

这里的 Index 指的是一个由 (keyVal, tupleID) 对组成的文件，一般 keyVal 和 tupleID 个占 4 Bytes：

这是一个用以标识每个 Tuple 在 Data File 中位置的额外数据结构 (Auxilary Data Structure)。值得注意的是，上图中的 Data Pages 是未排序的，但是 Index File 一定是根据 keyVal 排序的。

现在，我们主要来关注 1-d Index，即基于单个属性 A 的值。这个属性 A：

• 有可能时 Data File 的 Sort Key
• 有可能其取值是不重复的 (Unique)

因此，基于该属性 A 的一些特性，我们可以把 Index 分为以下几类：

1. Primary：属性 A 的取值不重复 (Primary Key)，且 Data File 可能基于其进行排序
2. Clustering：属性 A 的取值有重复 (Non-primary Key)，但是 Data File 基于其排序
3. Secondary：Data File 不基于 A 进行排序

给定的表可能具有基于多个属性的多个索引。

Index 也可以通过不同的方法进行结构化：

1. Dense：每个 Tuple 都由 Index File 中的条目引用
2. Sparse： 只有一部分 Tuple 都由 Index File 中的条目引用
3. Single-level：Tuples 通过 Index File 直接访问
4. Multi-level：需要访问多个 Index Pages才能得到 Tuple

因此，Index File 会有 i 个 Pages，显然这里的 i 一定远远小于 Data File 的 b Pages。同时 Index File 的每个 Page 的容量为 c_i (c_i >> c)。根据这些定义，我们可以知道：

Dense Index：i = ceil(r / c_i)

Sparse Index：i = ceil(b / c_i)

Dense Primary Index

Data File 未排序，一个 Index 实体对应一个 Tuple：

Sparse Primary Index

Data File 已排序，一个 Index 实体对应一个 Page：

Selection with Primary Index

对于一个 One Typle Query，在有了 Index File 之后，只需要在 Index File 中直接对 keyVal 继续二分法搜索即可，在找到目标 Tuple 的 keyVal 之后，即可得到其 tupleID，据此即可得到其所在 Page 的 ID：

ix = binary search index for entry with key K
if nothing found { return NotFound }
b = getPage(pageOf(ix.tid))
t = getTuple(b,offsetOf(ix.tid))
	-- may require reading overflow pages
return t

其代价为：

最坏的情况下 log₂ i Index Pages Read + (1 + Ov) Data Pages Read，因此：

Cost_one,prim = log₂ i + 1 + Ov

对于 Range Query：

1. 使用 Index Search 找到下界 (Lower Bound)
2. 顺序读取 Index，直到找到上界 (Upper Bound)
3. 累计一组要检查的 Bucket
4. 检查每个 Bucket 以找到匹配的 Tuples**（直到这一步才开始读取 Data Pages）**

具体的过程如下：

// e.g. select * from R where a between lo and hi
pages = {} results = {}
ixPage = findIndexPage(R.ixf,lo)
while (ixTup = getNextIndexTuple(R.ixf)) {
	if (ixTup.key > hi) break;
	pages = pages ∪ pageOf(ixTup.tid)
}
foreach pid in pages {
	// scan data page plus ovflow chain
	while (buf = getPage(R.datf,pid)) {
		foreach tuple T in buf {
			if (lo<=T.a && T.a<=hi)
			results = results ∪ T
} 	}	 }

对于 Partial Match Retrieve，其操作和 One Type Query 基本一致。 需要注意的是，如果一个 Query 不涉及 Primary Key，那么此时 Index 不会给我们任何帮助，只能线性扫描整个 Data File。

Insertion with Primary Index

现在来看 Insertion 操作。主要的过程是，首先将 Tuple 插入到合适的 Page P 的位置 p 上，得到该 Tuple 的 ID，之后在 Index File 中寻找新实体的合适位置，将新的 Index 实体 (k, tid) 插入到该位置。

tid = insert tuple into page P at position p
find location for new entry in index file
insert new index entry (k,tid) into index file

这里有一个问题需要注意。那就是我们必须保证 Index 实体的顺序不会被打破，这就有 2 种方法。第一，在 Index File 中创建 Overflow Pages；第二，将一部分 Index 实体顺延以进行重新排布。

如果使用后一种方法，那么我们平均需要读/写一半的 Index File Pages，所以代价为：

Cost_insert,prim = (log₂i)_r + i/2 (1_w + 1_r) + (1 + Ov)_r + (1 + δ)_w

• (log₂i)_r ：使用 Binary Search 找到新的 Index 实体应该被放置的 Index File Page 的代价
• i/2 (1_w + 1_r) ：读/写一半的 Index File Pages 的代价
• (1 + Ov)_r：读取对应 Data File Page 及其 Overflow Page 找到合适的插入位置
• (1 + δ)_w：将更新后的 Page 写回 Disk 的代价。这里的 δ 可以是 0、1、1 + Overflow Pages

Deletion with Primary Index

Deletion 操作首先需要使用 Index 找到目标 Tuple，之后将该 Tuple 标记为 “已删除”，最后将 Index File 中对应该 Tuple 的 Index 实体删除。

find tuple using index
mark tuple as deleted
delete index entry for tuple

而在删除 Index 实体时，同样也有两种选择：1. 标记；2. 顺延以进行重新排布。这两者的代价分别为：

1. Mark：Cost_delete,prim = (log₂i)_r + (1 + Ov)_r + 1_w + 1_w
2. Reorganisation：Cost_delete,prim = (log₂i)_r + (1 + Ov)_r + i/2(1_r + 1_w) + 1_w

Clustering Index

Data Files 排序，一个 Index 实体对应一个 Key Value。 注意，此时的 Index 不再基于 Primary Key，换言之，此时的属性 A 会有重复的取值，此时 Index File 中的每个实体只会指向重复取值的第一个 Page：

此时的 Deletion 操作需要格外注意，因为具备相同 Key Value 的 Tuple 会有多个，因此必须等所有这些 Tuple 都被删除时，才能把 Index File 中的对应 Index 实体删除。比如，必须将 Data File 中所有具备 k2 的 Tuple 删除，才能将 Index File 中的 key=k2 的实体删除。

Secondary Index

Data Files 未排序，同时属性 A 也不是 Primary Key。

在上图中属性 A 有三种不同的取值，Main Index File 是这三种取值的 Index，而 Secondary Index 则更进一步，将这三种取值的具体 Tuple 进行索引，可以看到，在 3 个不同 Pages 中具有 k1 取值的 Tuple 被 Secondary Index 索引了。 所以，我们在使用时，需要先搜索 Main Index File，然后再根据 Secondary Index 去找到 Tuple 的具体位置。其代价为：

Cost_pmr = (log₂ i_ix1 + a_ix2 + b_q (1 + Ov))

• log₂ i_ix1 是在 Main Index 中进行二分法搜索的代价
• a_ix2 是在 Secondary Index 的连续 Pages 中线性搜索的代价
• b_q (1 + Ov) 是在 Data File 中那些包含目标 Tuple 的 Pages 及其 Overflow Pages 中搜索的代价

Secondary Index 使用 2 个 Index Files 可以提升搜索的效率，其中 b_ix1 << b_ix2 << b。该方法还可以进一步提升。比如，可以把 Ix1 变为 Sparse Index，因为 Ix2 一定是有序的，此时 b_ix1 = ceil(b_ix2/c_i)。Secondary index 是 Multi-level Index 的基本形式，可以增加更多的 Index File，但是我们需要保证最顶层的 Index 一定是最小的，极限情况下，顶层 Index 只有一个 Page：

此时对于 One Type Query，具体的操作过程为：

xpid = top level index page
for level = 1 to d {
	read index entry xpid
	search index page for J'th entry
		where index[J].key <= K < index[J+1].key
	if (J == -1) { return NotFound }
	xpid = index[J].page
}
pid = xpid // pid is data page index
search page pid and its overflow pages

其代价为：Cost_one,mli = (d + 1 + Ov)_r

B-Trees

B-Tree 是一个具有以下属性的多路搜索树：

• 它们进行更新时仍保持平衡
• 每个 node 中至少有 (n-1)/2 个实体
• 每个 tree node 占据一整个 disk page

在 B-Tree 中的 Insertion 和 Deletion 操作可以被很高效地实现。相比于一般的多路搜索树，B-Tree 具有以下优势：

1. 更好的存储利用率（约有 2/3 是满的）
2. 最坏情况下有更好的表现（更浅）

下图是一个 B-Tree 的例子，其中 depth=3，n=3

这里我们的 B-Tree 实际上是一个 B+ Tree，与一般的 B-Tree 不同的地方在于，B+ Tree 仅有 Leaf Node 可以与 Data Pages 交互，而 B-Tree 中的所以节点都可以与 Data Pages 交互。 上图的每个 node 中，上半部分是 Key，下半部分是 Pointer，根据条件指向不同的 Node，比如 k<23 node 中的第一个指针指向 k<7，第二个指针指向 7 ≤ k ＜13 … 而 - 则表示该 Node 中的 Free Slot，可以看到，所有的 node 都是 Half Full 的，除了 root node 是个例外。

B-Tree Depth

B-Tree 的深度取决于分支因子 (Branching Factor)，即每个 node 的满载程度。一般来说，B-Tree 中的 node 满载程度为 69% 左右。所以，负载 L_i = 0.69 × c_i ，树的深度约为 ceil(log_Li r)。比如：我们定义节点容量为 c_i = 128，那么 L_i = 0.69 × 128 ≈ 88。

Selection with B-Trees

对于 One Type Query，此时仅有一个结果会被返回。 使用 B-Tree 进行搜索只需要从 root node 开始向下搜索，直到在某个 leaf node 找到满足要求的结果

Node find(k,tree) {
	return search(k, root_of(tree))
}
Node search(k, node) {
	// get the page of the node
	if (is_leaf(node)) return node
	keys = array of nk key values in node
	pages = array of nk+1 ptrs to child nodes
	if (k <= keys[0])
		return search(k, pages[0])
	else if (keys[i] < k <= keys[i+1])
		return search(k, pages[i+1])
	else if (k > keys[nk-1])
		return search(k, pages[nk])
}

该搜索过程简单来说就是：从 root node 开始进行搜索，在到达 leaf node 之前，根据条件不断向下寻找 child node，当我们得到一个 leaf node 之后，在该 node 中找到对应的 Index 实体，使用该实体中的 tupleID 来访问 data file 中对应的 tuple。因此，其代价 Cost_one = (D + 1)_r ，及深度 + 1.

对于 Range Query，此时返回的不止一个。 对范围的下界 (Lower Bound) 进行树搜索，再得到某个 leaf node 之后，通过 leaf node 之间的联系（指针）向后继续搜索，直到找到上界 (Upper Bound)。比如，在下图中，我们 SELECT * FROM Relation r WHERE r.id ≥ 11 AND r.id < 25;

此时，先搜索下界 11，此时到达第二个 leaf node，在其中找到 11 之后，向后继续搜索下一个（右边）的 leaf node，直到找到上界。这也是为何我们在图中画出 leaf node 之间存在指针的原因。所以，代价 Cost_range = (D + b_i + b_q)_r

Insertion into B-Trees

Insertion 操作大致上为：

1. 找到合适的 leaf node，并且其中 new key 应当放置的位置；
2. 如果该 node 未满，直接进行插入
3. 如果该 node 已满：
   • 将中间元素提升为父元素
   • 把该 node 分割 (split) 为两个 half-full nodes
   • 把新的 key 插入到合适的 half-full nodes 中
4. 如果父节点也满了，那就继续分割，向上操作
5. 如果已经到了 root node，并且 root node 也没有 free slot 了，那就向上创建一个新的 root node

同样根据一个具体的例子来看，在下图的 B-Tree 中插入 12, 15, 30, 10：

插入 12 时，从 root node 开始搜索，找到第 2 个 leaf node，此时该 node 有 free slot，直接将 12 插入。接下来时 15，同样从 root node 开始搜索，找到第 3 个 leaf node，此时也有 free slot，为了保证 Index Page 中的顺序不被打破，将其插入在 13 和 17 之间。插入 30 的操作也基本一致。

接下来插入 10，依旧从 root node 开始搜索，但是找到的 leaf node 2 已经满了，此时将该节点的中间元素 11 升格为父元素，放入该 leaf node 的父节点中，同时，将右边的 12 放入一个新的 leaf node（11 也在其中），此时 10 已经可以安心放在分割后的左边 leaf node 中：

在了解了 insertion 操作的过程之后，可以看出，该操作的代价主要分为三个部分：

Cost_treeSearch + Cost_treeInsert + Cost_dataInsert

最好的情况下，只需要写一个 Data Page，即从 root node 开始遍历，找到的 leaf node 有足够的空间，读写 data page，写一个 index page（注意此处的顺序，data page 的读写在前面）

Cost_insert = D_r + 1_w + 1_w + 1_r

一般的情况下，需要重新排布 2 个 leaf nodes 和 1 个 parent node。同样从 root node 开始遍历，把遍历的 nodes 保存在 buffer 中，找到 leaf node 之后，先读/写 data page，再更新/写 leaf node 和 parent node

Cost_insert = D_r + 3_w + 1_w + 1_r

最坏的情况下，一直回溯到 root node。从 root node 遍历到 leaf node，读/写 data page。更新/写 leaf node 和 parent node，重复该操作 D - 1 次。

***Cost_insert = D_r + D · 3_w + 1_w + 1_r***

PostgreSQL 中的 B-Tree 叫作 Lehman/Yao-style B-trees。是一个能在高并发环境下高效工作的变体。

Multi-dimensional Search Trees

我们目前了解了对于单一属性构建 B-Tree 并进行搜索的方法，现在来看看多个属性的情况。在过去的 20 年中，各种不同的 Multi-dimensional Tree 被提出，这些 Tree 的主要区别在于对于 Tuple Space 的分割方法。其中比较主要的 3 种是 kd-trees, Quad-trees 和 R-trees.

先来看 Tuple Space。我们假设之后讨论的数据都来自以下 Relation：

create table Rel (
X char(1) check (X between ‘a’ and ‘z’),
Y integer check (Y between 0 and 9)
);

样例元组就有：

R(‘a’,1) R(‘a’,5) R(‘b’,2) R(‘d’,1)
R(‘d’,2) R(‘d’,4) R(‘d’,8) R(‘g’,3)
R(‘j’,7) R(‘m’,1) R(‘r’,5) R(‘z’,9)

对于上面这些样例元组，可以得到一个如下的 Tuple Space：

kd-Trees

对于上面得到的那个 Tuple Space，我们该如何进行多属性搜索呢？kd-Trees 是一种多路搜索树：

• 树的每一层都基于不同的属性进行分隔 (Partition)
• 每个节点包含 (n-1) 个 Key Values 以及指向 n 个子树的 Pointers

在上图中，root node 依据属性 X 决定向下走向哪条分支。第二层的 node 则依据属性 Y 决定向下分支。在第三层，再次根据属性 X 来进行分隔。 比如，我们需要检索 Tuple (a, 5)，那么就需要从根节点开始，先根据属性 X = a 确定走左分支，然后再根据属性 Y=5 确定走右分支，最后根据属性 X = a < c 得到最后的 leaf node。 根据这棵树的不同层级 (level)，我们会把在同一 leaf node 中的 Tuples 分在一起：

上述的搜索就可以表示为：

// Started by Search(Q, R, 0, kdTreeRoot)`
Search(Query Q, Relation R, Level L, Node N)
{
	if (isDataPage(N)) {
		Buf = getPage(fileOf(R),idOf(N))
		check Buf for matching tuples
	} else {
		a = attrLev[L]
		if (!hasValue(Q,a))
			nextNodes = all children of N`
		else {
			val = getAttr(Q,a)
			nextNodes = find(N,Q,a,val)
		}
		for each C in nextNodes
			Search(Q, R, L+1, C)
} }

这里我们需要注意标注的两行，如果 Query Tuple 对于当前层的属性没有值，那么就需要将之后的所有 Child Node 进行搜索。比如，在上面的树中，我们想要查询 (d, )，此时在第一层可以根据属性 X 确定走左边的支路，但在第二层，因为我们没有属性 Y，所以将下面支路的所有 node 进行搜索。在左支路，再次根据 X=d 判断走右支路，得到一个 leaf node；同样，在右支路也根据 X=d 判断走右支路，的到另一个 leaf node

Quad Trees

Quad Tree 在 Tuple Space 中进行规则 (Regular) 且不相交 (Disjoint) 的分割。

• 对于一个 2 维空间，总是分为 North East, North West, South West, South East 四个区域
• 每个分区可以再进一步分为 4 个

上图中的红线表示顶层分割，绿线表示第二层进行的分割，蓝线表示第三层进行的分割。此时再每个子区间内，都不会有多于 2 个 Tuples。这也是为何我们对左边两个用红线分割出的子区域进行在分割的原因，如果不进行分割，那么子区间内的 Tuple 数量会大于 2。 对于分割，我们有以下几个定义：

• 一个子区如果其中再没有任何子区，那么该子区就是 leaf quadrant
• 每个 leaf quadrant 对应一个 Data Page
• 需要不断分割，直到每个子区中的点能够放入一个 Data Page
• 最理想的情况是每个子区中的点数都相同，此时就是平衡
• 由于在 Tuple Space 中，Tuple Point 的空间密度 (Density) 不均匀，因此在不同的区域需要及逆行不同程度的分割，这就意味着树不一定要是完美平衡de

上面的分割可以给我们一个如下图所示的 tree：

在 Quad Tree 中的搜索也被称为 Space Query (空间查询)。比如我们想要查询的 Tuple，它的属性 A1 ∈ [e, k]，A2 ∈ [1, 3]，那么此时就可进行如下搜索：

图中的虚线框就是我们的查询。该查询与 GREEN(all), RED(NW), BLUE(NE, SE) 有交集，因此只需要扫描这部分即可。所以，在 Quad Tree 中的搜索就是在 Query Area 与 Space 的重叠区域找到所有的 Tuple Point，如果是 leaf node，则检查对应 Data Page 中是否有匹配的 Tuple，否则继续搜索

R-Trees

R-Tree 使用更加灵活的方法，此时对于 Tuple Space 的分割可以存在重叠，这就与前两种 Tree 有明显的差异，因为前两者的分割都是 Disjoint，换言之，分区之间不会有重叠。

• 树中的每个 node 表示一个 k 维的超立方体（2 维空间中就是一个二维的长方形）
• 它的子区域中会有重叠
• 子区域无需覆盖整个 Parent Region

这样的作法可以优化空间分配和数据分配，同时，每个区域中会有相似数量的 Tuple Point

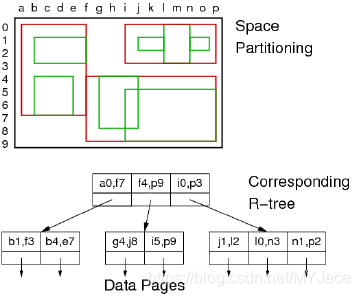
上图中的红框表示 Top Level 的分割，其中的绿框表示它的子区域。

先来看 Insertion 操作：

1. 从 root node 开始，寻找一个能完全包含插入对象 R 的区域
2. 如果没有子区域能够完全包含 R，那么就挑选一个子区域，拓展它的边界以使其能够包含 R
3. 如果有多个子区域能够完全包含 R，就从中挑选一个，然后继续向下操作
4. 一旦我们到达了某个具体的 Data Page，就可以进行插入
5. 如果 Data Page 没有足够的空间，那就使用 2 个 Data Pages。把插入对象分割，分别放入 2 个 Data Pages（与 B-Tree 的操作类似）

在 R-Trees 中的查询分为两类：

1. “Where-am-I”：找到所有包含给定点 P 的区域。这就需要从 root node 开始，寻找所有子区域包含 P 的节点。递归在 node 中搜索，直到找到一个 leaf node
2. Space Query：处理与前一个类似。只是现在找的是与目标区域重叠的区域

Costs of Search in Multi-d Trees

在 Multi-d Tree 中搜索的代价与树的结构和查询类型相关。

如果是 Partial Match Retrieve 且所有的属性都有确定值，那么：

在 kd-Tree 和 quad-Tree 中，代价都为 depth D

在 R-Tree 中，可能会有多条路径

但通常情况下，经常会有一部分属性的值是不确定的。

Multi-dimensional Hashing

在上一周我们已经了解了如何对单一属性进行哈希及之后的一系列操作。现在，我们要来看对于多个属性进行哈希。先来考虑一个 Partial Matching Retrieve：

select * from R where a₁ = C₁ and … and a_n = C_n

如果在条件中的一系列属性 a_i 中存在 Hash Key，那么，该查询就会变得十分高效。而如果没有任何一个 a_i 是 Hash Key，那么就只能进行线性扫描。当然，此时我们也可以选择使用多属性哈希 (Multi-attributes Hashing) 来进行缓解。即在查询时形成一个包含所有属性的复合哈希值 (Composite Hash)，复合哈希的某些组件是已知的（帮助我们限制需要检查的 Data Pages 的数量）

下面来看多属性哈希的一些具体参数：

• 用 b = 2^d 表示 Data File 的 Pages 数量（Hash Value 有 d 位）
• Relation 有 n 个属性：a₁, …, a_n
• 属性 a_i 有 Hash Value h_i(a_i)
• 属性 a_i 在组合哈希 (Combined Hash Value) 中占据 d_i bits
• d = Σ d_i
• 一个选择向量 (Choice Vector, CV) 声明了 k 位 Hash Value，我们需要知道其中每一部分的地址

下面看一个具体的例子：

考虑一个 Relation：Deposit(branch,acctNo,name,amount)

同时，该 Relation 的 Data File 仅有 8 个 Data Pages

因此，只需要 d = 3 即可完整表示所有的 Pages (2³ = 8)。因此，此时的 Combined Hash Value 只需要 3 位，我们选择前三个属性即可，即 d₁ = d₂ = d₃ = 1，d₄ = 0。换言之，我们现在忽略属性 amount，所以可以假设，不会有形如：

SELECT * FROM Deposit WHERE amount=253；

之类需要属性 amount 的查询。这样的查询不会得到 Hashing 的帮助，依旧需要线性扫描

因此，现在的 Choice Vector

Hash Value 中的 bit 0 来自 hash₁(d₁) 的 bit 0

Hash Value 中的 bit 1 来自 hash₂(d₂) 的 bit 0

Hash Value 中的 bit 2 来自 hash₃(d₃) 的 bit 0

Hash Value 中的 bit 3 来自 hash₁(d₁) 的 bit 1

比如一个具体的 Tuple 为：

此时，对每个属性进行哈希，得到 4 个哈希值，我们从前三个取对应位置的值组成 Combined Hash Value：

这里给出组成该 Combined Hash Value 的 Hash Function：

#define MaxHashSize 32
typedef unsigned int HashVal;
// extracts i'th bit from hash value
#define bit(i,h) (((h) & (1 << (i))) >> (i))
// choice vector elems
typedef struct { int attr, int bit } CVelem;
typedef CVelem ChoiceVec[MaxHashSize];
// hash function for individual attributes
HashVal hash_any(char *val) { ... }

先定义 Choice Vector，这个 Vector 是 int pair 的序列，每个 pair 的第一个元素指定值来自哪个 Attribute，第二个值指定来自第几位。之后需要对不同的 Attribute 使用不同的 Hash Function，得到每个 Attribute 的 Hash Value。写成代码形式为：

HashVal hash(Tuple t, ChoiceVec cv, int d)
{
	HashVal h[nAttr(t)+1]; // hash for each attr
	HashVal res = 0, oneBit;
	int i, a, b;
	for (i = 1; i <= nAttr(t); i++)
		h[i] = hash_any(attrVal(t,i));
	for (i = 0; i < d; i++) {
		a = cv[i].attr;
		b = cv[i].bit;
		oneBit = bit(b, h[a]);
		res = res | (oneBit << i);
	}
	return res;
}

Queries with MA.Hashing

对于 Partial Match Query，我们知道一部分 Attribute 的值，但是还有一部分未知。比如：

select amount
from Deposit
where branch = 'Brighton' and name = 'Green'

此时我们知道 (Brighton, ?, Green, ?)。为了解决这类问题，我们首先来看一个更简单的问题：

select amount from Deposit where name=‘Green’

此时我们仅知道 Attribute name 的值为 ‘Green’，但是根据前面所说，我们需要构建一个 Combined Hash Value，因此就有：

我们现在能做的只有将所有可能的哈希值都找出来，这里就是 100，101，110，111. 那么在这几个 Pages 中一定有符合条件的 Tuples。那么，对于 2 个条件该如何处理就已经很清楚了。

多属性哈希可以处理多种不同的查询，一个有 n 个 Attributes 的 Relation 会有 2ⁿ 种不同的查询，而这些不同的查询就会有不同的代价：

Cost(Q) = 2^s 这里的 s = Σ d_i (i !∈ Q)

Query Distribution 可以大大帮助我们提升查询效率，所谓的 Query Distribution 会给出提出每种 Query 的概率 P_Q。可以用一个例子来看，假设对于某个 Relation 有以下几种 Query：

select * from R where a=1
select * from R where d=2
select * from R where b=3 and c=4
select * from R where a=5 and b=6 and c=7

其中第一种比较常见，而第三种比较少见，那么在 Combined Hash Value 中就可以给 Attribute a 更多的 bits，而后两种更少的 bits。现在来看具体的代价：

如果所有的 Attribute 值都已知，那么 Min Cost_pmr = 1

如果所有的 Attribute 值都未知，那么 Max Cost_pmt = 2^d = b

平均代价为所有查询类型的加权求和：Avg Cost_pmr = Σ p_Q ∏ 2^di （i !∈ Q）

除了上述的 Query Distribution，还有其他方法来优化多属性查询效率：

1. Attribute Domain 的规模，比如一个 Attribute 的取值只有 4 个，那么就不会给他安排多于 2 个 bits
2. Discriminatory Power，如果某个 Attribute 比其他 Attribute 更具辨识度，即取值更加不重复，那么就给他分配更多的 bits

Signature-based Indexing

我们目前为止介绍的多个方法确实能够减少 Data Pages 的读取数量，但都是针对单一 Attribute 的情况。现在我们就来看一种针对 Partial Matching Query，即有着多个等价条件测试的查询的方法，叫作：Signature-based Indexing (基于签名的索引)：

1. 该方法不会获得优于 O(n) 的性能表现
2. 它实际上还是线性扫描 (Linear Scan)，只不过不是直接对 Data File 进行线性扫描，而是对一个比 Data File 小得多的文件进行扫描，这个文件就由 Signature (签名) 组成

现在来看，什么是 Signature (签名)。每个 Tuple 都会与一个 Signature 相关联：

• Signature 是一种紧凑型描述器 (Compact Descriptor)。但是它也是有损的 (Lossy)，所以两个不同的 Tuple 有可能会有相同的 Signature
• Signature 的组成有些类似多属性哈希，也是结合了从多个属性得到的信息
• 所有的 Signature 都被存储在一个 Signature File 中，该 File 与 Data File 并行。在对 Data File 进行扫描之前，我们会优先对 Signature File 进行扫描以期能够筛选掉一部分不符合条件的 Tuples

我们用一张图来详细理解 Signature 和 Signature File：

可以看到，Signature File 与 Data File 并存，Data File 中的每一个 Tuple Slot 对应一个 Signature，未被使用的 Signnature Slot 被清零。但是，Signature 不会告诉我们一个 Record/Tuple 应该被放置在哪里，所以，可以同时使用其他的 Hashing 方法。

一个 Signature 就是从一个 Tuple 中汇总 (Summarise) 出来的数据，这个 Tuple 有 A₁ … A_n 共 n 个属性。我们现在定义一个 code word cw(A_i)，它是 Attribute A_i 的哈希值，所以，本质上就是一个 Bit String，这个 String 长 m bits，其中有 k bits 被置为1 (k << m)。 一个 Signature 就由 n 个 Attribute 的 code word 组成，具体组合的方式有 2 种：1. 叠放 (Overlay)，2. 拼接 (Concatenate)，同时，我们希望 Signature 中有一半的 bits 会被置为 1。

生成一个 k-in-m 的 code word 的具体过程为：

bits codeword(char *attr_value, int m, int k)
{
	int nbits = 0; // count of set bits
	bits cword = 0; // assuming m <= 32 bits
	srandom(hash(attr_value));
	while (nbits < k) {
		int i = random() % m;
		if (((1 << i) & cword) == 0) {
			cword |= (1 << i);
			nbits++;
		}
	}
	return cword; // m-bits with k 1-bits and m-k 0-bits
}

Superimposed Codewords (SIMC) - 叠加码字

在一个叠加 Codeword 中，signature 由各属性的 codewords 叠放组成 （位或运算）

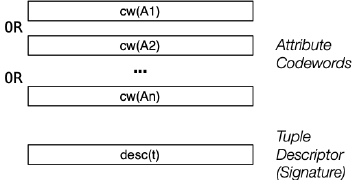
对于一个 Tuple 的叠加码字形式的 signature desc(t) ：

• 它是一个 bit-string，长度为 m bits，其中 j ≤ nk(≈ n/2) bits 被置为 1
• desc(t) = cw(A_i) OR cw(A₂) OR … OR cw(A_n)

具体的实现方式我们上面已经讲过，代码如下所示：

Bits desc = 0
for (i = 1; i <= n; i++) {
	bits cw = codeword(A[i],m,k)
	desc = desc | cw
}

Concatenated Codewords (CATC) - 拼接码字

在一个拼接 Codeword 中，signature 由各属性的 codewords 拼接组成

对于一个 Tuple 的叠加码字形式的 signature desc(t) ：

• 它是一个 bit-string，长度为 m bits，其中 j = nk(≈ n/2) bits 被置为 1
• desc(t) = cw(A_i) + cw(A₂) + … + cw(A_n)

对于每一个 codeword，长度为 p = m/n，其中，有 k bits 被置为 1.

Queries using Signature

在基于 Signature 的索引中，回答查询 q 有以下几个步骤：

1. 首先生成一个 Query Descriptor desc(q)
2. 接着，在 Signature File 中使用 desc(q) 进行扫描
3. 如果 signature_i 匹配 desc(q)，那么 Tuple i 就应该是一个可能匹配的对象

其中，desc(q) 是由已知的 Attributes 的 codewords 组成的，对于任何未知的 Attribute A_i，cw(A_i) = 0。现在给出具体的搜索过程代码：

pagesToCheck = {}
// scan r descriptors
for each descriptor D[i] in signature file {
		if (matches(D[i],desc(q))) {
			pid = pageOf(tupleID(i))
			pagesToCheck = pagesToCheck ∪ pid
		}
}
// scan bq + δ data pages
for each pid in pagesToCheck {
		Buf = getPage(dataFile,pid)
		check tuples in Buf for answers
}

核心的思想正如之前所说：不直接扫描 DataPages，而是在 Signature File 中找到匹配的 Signature，再通过这些 Signature 找到对应的 Tuple，以及 Tuple 所在的 Page。最后对这些 Page 进行搜索即可。

这里我们需要格外注意一点，那就是不管用上述哪种索引方式，都会有 False Match 的情况出现，这也是 Hashing 这个方法本身的缺点，那就是不同的 Tuple 也可能会有一样的 Hash Key。所以这就会导致 desc(q) 与 D[i] 匹配，但是找不到符合要求的 Tuple。为了使这样的情况尽可能少出现，就需要选择合适的 m 和 k，m 尽可能要小，m 越大意味着要读的 signature data 越多。

SIMC（叠加码字）	CATC（拼接码字）
m-bits 长，有一半的 bits 置为 1	m-bits 长，有一半的 bits 置为 1
其中的 codewords 应有 m/2n bits 置为 1	其中的 codewords 应有 m/2n bits 置为 1
每个 codeword 长度为 m，更长的 codeword 意味着更少的哈希冲突 (Hash Collision) 但会有叠放冲突 (Overlay Collision)	每个 codeword 长度为 m/n，更短的 codeword 意味着更多的哈希冲突 (Hash Collision)

需要注意的是，在 CATC 中，实际上并不需要保证所有的 codeword 长度相同 (m/n)，实际上只需要保证长度之和为 m 即可。