吴恩达机器学习（二）

7.正则化

7.1 过拟合的问题

当把学习算法应用到某些特定的机器学习应用时，会遇到过拟合（over-fitting）的问题，导致它们效果很差。以及我们会谈论一种正则化（regularization）的技术，它可以改善或者减少过拟合问题。

第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质；预测新数据。

在分类问题中也存在这样的问题：

就以多项式理解，x次数越高，拟合的越好，但相应的预测的能力就可能变差。

问题是，如果我们发现了过拟合问题，应该如何处理？

1. 丢弃一些不能帮助我们预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（eg. PCA）
2. 正则化。保留所有的特征，但是减少参数的大小（magnitude）

7.2代价函数

上面的回归问题中如果我们的模型是：

我们可以从之前的示例中看到，正是那些高次项导致了过拟合的产生，如果我们能让这些高次项的系数接近于0的话，我们就能很好的拟合了。

所以我们要做的就是在一定程度上减小这些参数θ的值，这就是正则化的基本方法。我们决定要减少θ3和θ4的大小，我们要做的便是修改代价函数，在这两个参数上设置一点惩罚。这样做的话，我们在尝试最小代价时也需要将这个惩罚纳入考虑中，并最终导致选择较小一些的θ3和θ4。

修改后的代价函数如下：

假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：

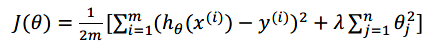
其中λ又称为正则化参数（Regularization Parameter） 注：我们不对θ0进行惩罚。

如果选择的正则化参数λ过大，则会把所有的参数都最小化了，造成欠拟合。

所以对于正则化，我们要取一个合理的λ的值，这样才能更好的应用正则化。

7.3正则化线性回归

对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。

正则化线性回归的代价函数为：

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对进行正则化，所以梯度下降算法将分两种情形：

对于上面的算法中j = 1，2，，，，n时更新式子进行调整可得：

可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在有算法更新规则的基础上令θ值减少了一个额外的值。

我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下：

7.4正则化的逻辑回归模型

我们也给代价函数增加一个正则化的表达式，得到代价函数：

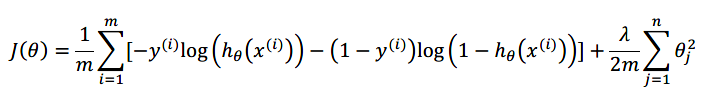
要最小化该代价函数，通过求导，得出梯度下降算法为：

注：看上去同线性回归一样，但是知道，是与线性回归不同

8.非线性假设

8.1非线性假设

无论是线性回归还是逻辑回归都有这样一个缺点，即：当特征太多时，计算的负荷会非常大。

假设我们有非常多的特征，大于100个，我们希望用这100个特征来构建一个非线性的多项式模型，结果将是非常惊人的特征组合。

假设我们希望训练一个模型来识别视觉对象，我们怎样才能这么做呢？一种方法是我们利用很多汽车的图片和很多非汽车的 图片，然后利用图片上的一个个像素的值（饱和度或亮度）来作为特征。

假如我们只选用灰度图片，每个像素则只有一个值，我们可以选取图片上的两个不同位置上的两个像素，然后训练一个逻辑回归算法利用这两个像素的值来判断图片上是否是汽车：

假使我们采用的都是50*50像素的小图片，并且我们将所有的像素视为特征，则会有2500个特征，如果我们要进一步将两辆特征组合构成一个多项式模型，则会有约2500^2/2个，普通的逻辑回归模型，不能有效处理那么多特征，这时候我们需要神经网络。

8.3模型表示1

为了构建神经网络模型，我们需要思考大脑中的神经网络是怎样的？每一个神经元都可以被认为是一个处理单元/神经核，它含有许多输入/树突，并且有一个输出/轴突。神经网络是大量神经元互相链接并通过电脉冲来交流的一个网络。

神经网络模型建立在很多神经元之上，每一个神经元又是一个个学习模型。这些神经元（激活单元）采纳一些特征作为输出，并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例，在神经网络中，参数又可被称为权重

其中x1,x2,x3是输入单元，我们将原始数据输入给它们。

a1,a2,a3是中间单元，它们负责将数据进行处理，然后呈递到下一层。

最后是输出单元，它负责计算

神经网络模型是许多逻辑单元按照不同层级组织起来的网络，每一层的输出变量都是下一层的输入变量。中间一层是隐藏层。我们为每一次都增加一个偏差单位

对于上图的模型，激活单元和输出分别表达为：

每一个a都是由上一层所有的x和每一个x所对应的决定的

前向传播算法。

8.4模型表示2

向量化，以第二层为例

第五周

9、神经网络的学习

9.1 代价函数

9.2 反向传播算法

现在，为了计算代价函数的偏导数，我们需要采用一种反向传播算法。

现假设我们的训练集只有一个实例（x,y）,我们的神经网络是一个四层的神经网络，其中K=4，S_L = 4,L=4

前向传播算法：

我们从最后一层的误差开始计算，误差是激活单元的预测与实际值之间的误差。

假设λ = 0，即我们不做任何正则化处理时有：

关于反向传播公式的推导

如果我们考虑正则化处理，并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中，我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中，我们同样需要计算每一层的误差单元，但是我们需要为整个训练集计算误差单元，此时的误差单元也是一个矩阵，我们用来表示这个误差矩阵。第l层的第i个激活单元收到第j个参数影响而导致的误差：

即首先先用正向传播方法计算出每一层的激活单元，利用训练集的结果与神经网络预测的结果求出最后一层的误差，然后利用该误差运用反向传播算法出直至第二层的所有误差。

在求出之后，我们便可以计算代价函数的偏导数了，计算方法：

9.4 实现注意：展开参数

这段视频中，介绍了一个细节的实现过程，怎样把参数从矩阵，展开成向量，以便我们在高级最优化步骤中的使用需要

9.5梯度检验

当我们对一个较为复杂的模型（eg神经网络）使用梯度下降算法时，可能会存在一些不容易察觉的错误，意味着，虽然代价看上去不断减小，但最终的结果可能并不是最优解。

为了避免这样的问题，我们采取一种叫做梯度的数值检验（Numerical Gradient Checking）。这种方法的思想是通过估计梯度值来检验我们计算的到数值，是否真的是我们要求的。

对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点，然后计算两个点的平均值以估计梯度。即即对于某个特定的θ，我们计算出在θ-ε，和，θ+ε的代价值（ε是一个非常小的值，通常选取0.001），然后求两个代价的平均，用以估计在θ初的代价值。

当θ是一个向量时，我们则需要对偏导数进行检验，因为代价函数的偏导数检验只针对一个参数的改变进行检验，下面是一个只针对θ1进行检验的实例：

最后我们还需要通过反向传播方法计算出的偏导数进行检验。

根据上面的算法，计算出的偏导数存储在矩阵中。检验时，我们要将该矩阵展开成向量，同时我们也将θ矩阵展开为向量，我们针对每一个θ矩阵展开为向量，我们针对每一个θ都计算一个近似的梯度值，将这些值存储于一个近似梯度矩阵中，最终将得出这个矩阵同进行比较。

9.6随机初始化

任何优化算法都需要一些初始的参数，到目前为止我们都是初始所有参数为0，这样的初始方法对于逻辑回归可行，但是对于神经网络来说是不可行的。如果我们令所有的参数都为0，这将意味着我们第二层的所有激活单元都会有相同的值，同理，如果我们初始化所有的参数都为一个非0的数，结果也是一样的。

我们通常初始参数为正负ε之间的随机值，假设我们要随机初始化一个尺寸为10*11的参数矩阵代码如下：

9.7综合起来

小结使用神经网络时的步骤：

网络结构：第一件事是选择网络结构，即决定选择多少层以及决定每层分别有多少单元。

第一层的单元数即我们训练集的特征数量。

最后一层的单元数是我们训练集的结果的类的数量。

如果引出层大于1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好。

我们真正要决定的是隐藏层数和每个中间层的单元数。

训练神经网络：

1.参数的随机初始化

2.利用正向传播方法计算所有的

3.编写计算代价函数J的代买//？

4.利用反向传播方法计算所有偏导数

5.利用数值检验方法检验这些偏导数

6.使用优化算法来最小化代价函数