Leetcode最大子序和算法与分析

@Leetcode最大子序和

最大子序和，以其经典、有教育性为很多人所数值，江湖或称“最大子段和”、“最长子段和”说的都是他，方法简单要用脑，编写清晰要小心，请看题干：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
进阶:如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

这怕是再简单过不的题干了，但是我们从中可以发现不少信息（可以使用分治法这个不算），比如说比较容易想到的算法只需要O(n) 的复杂度就行了，那么这个容易想到的算法究竟是什么呢，笔者在这里先给大家看看动态规划，也就是大佬们常说的dp算法。代码如下：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
    int com=0;
    int maxsum=INT_MIN;
    for(int i=0;i<nums.size();i++)
    {
        com=max(nums[i],com+nums[i]);
        maxsum=max(maxsum,com);
    }
    return maxsum;
    }
};

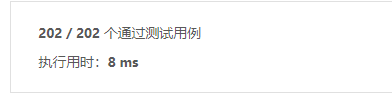
动态规划法的思路大概可以描述为：定义一个比较值和一个当前最大值，在循环中，如果加上当前元素的值会比之前的比较值大，就加上并将其变为新的比较值，然后将之前保存的最大值和这个比较值相比，进而更新这个最大值。注意初始化时要将最大值定为INT_MIN，是一个很小的值，这也是笔者新学的一招，是个小细节，不然的话，当测试样例很小时，小过你的初始值，就会出现问题啦。

那么进阶的算法也就是题中所说的分治法，是怎么一回事呢？借鉴了一下gpe3DBjDS1这位大佬的思想
链接：https://leetcode-cn.com/problems/two-sum/solution/zui-da-zi-xu-he-by-gpe3dbjds1/
请看代码：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size()==0) return NULL;
        return maxsubsum(nums,0,nums.size()-1);
    }
    int maxsubsum(vector<int>& nums,int left,int right){
    if(left==right)
        return nums[left];
    else
    {
        int center=(left+right)/2;
        int leftsum=maxsubsum(nums,left,center);
        int rightsum=maxsubsum(nums,center+1,right);
        int temp=nums[center];
        int maxcount=nums[center];
         for(int i=center-1;i>=left;i--)
        {
            temp+=nums[i];
            maxcount=max(maxcount,temp);
        }
        temp=maxcount;
        for(int i=center+1;i<=right;i++)
        {
            temp+=nums[i];
            maxcount=max(maxcount,temp);
        }
        return max(max(leftsum,rightsum),maxcount);
    }
   }
};

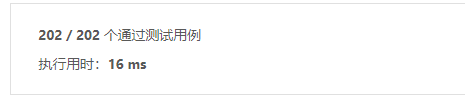
分治法是将整个子段分为了左右两个部分，并从最两端开始进行遍历，如果满足条件则定为加入计算的部分。整体思想上，分治法的情况大概有三种：
（1） a[1:n]的最大子段和与a[1:n/2]的最大子段和相同
（2） a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同
（3） a[1:n]的最大子段和为a[i]+…+a[j]，并且1<=i<=n/2，n/2+1<=j<=n。

对于（1）和（2）两种情况可递归求得，但是对于情况（3），容易看出a[n/2]，a[n/2+1]在最大子段中。因此，我们可以在a[1:n/2]中计算出s1=max(a[n/2]+a[n/2-1]+…+a[i]),0<=i<=n/2，并在a[n/2+1:n]中计算出s2= max(a[n/2+1]+a[n/2+2]+…+a[i])，n/2+1<=i<=n。则s1+s2为出现情况（3）的最大子段和。

上面的代码其实与这个思路并不完全一样他从某种意义上是将左边和右边整合了一下。需要注意一下center的处理细节，毕竟在循环中是边界值。我们可以从两个for循环之间的temp的直接赋值看到，右边整合实际上已经是将上面思路的(2)(3)结合在一起了，这样最后的判断只要对(1)(2)(3)做一个比较就行，省去了很多繁复的步骤和变量的定义，增加了代码的可读性，但是基本思路还是这样。

分治法的运行速度远远不如动态规划的算法，但两个方法的思路都值得我们学习，还有暴力循环的方法，这里笔者就不做分析了（太菜），以上思路都是仅供参考，真正的奥妙，得自己敲了才能明白。