深度学习——激活函数的原理与应用

1 概述

激活函数（Activation Function）在深度学习中起着至关重要的作用，它能为神经网络引入非线性因素，使得神经网络可以拟合各种复杂的非线性关系。常用的激活函数有 sigmoid、 tanh、 relu等。

2 激活函数的作用

• 引入非线性：在神经网络中，如果没有激活函数，无论有多少层神经元，整个网络都等价于一个线性变换模型，而线性模型的表达能力有限，无法处理像图像识别、语音识别等复杂任务中存在的高度非线性关系。激活函数通过对神经元的输出进行非线性变换，使得神经网络能够逼近任意复杂的函数，大大增强了网络的表达能力。
• 决定神经元是否激活：神经元接收输入的加权和，激活函数根据这个加权和的值来确定神经元是否被 “激活” 以及激活的程度，从而控制信息在网络中的流动与传递。

3 常见的激活函数

3.1 Sigmoid 函数

函数图像呈现出 S 形，输出值范围在 (0,1) 之间。例如，当 $x=0$ 时，$\sigma (0)=\frac{1}{2}$；当 $x$ 趋于正无穷时，$\sigma (x)$趋近于1；当 $x$ 趋于负无穷时，$\sigma (x)$趋近于0。其数学表达式为
$$\sigma (x)=\frac{1}{1+e^{-x}}$$
导数公式：
$${\sigma }^{\prime }(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=\sigma (x)(1-\sigma (x))$$

它能将输入值映射到一个概率区间，常被用于二分类问题的输出层，把神经元的输出解释为属于某一类别的概率。但它存在一些缺点，比如容易出现梯度消失问题（当 $x$ 取值绝对值较大时，导数趋近于0，导致反向传播时梯度更新缓慢甚至停止），并且输出不是以0为中心的，这可能会影响网络训练的效率。

而Softmax 在处理多分类问题时经常被用到。

3.2 Tanh 函数（双曲正切函数）

图像同样是 S 形，但输出值范围在 (-1,1) 之间，它是 Sigmoid 函数的一种变形。Tanh 函数的数学表达式如下：
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
或者等价地：
$$\tanh (x)=2\cdot \sigma (2x)-1$$
导数公式：
$${\tanh }^{\prime }(x)=1-{\tanh }^2(x)$$
相比 Sigmoid 函数，它的输出是以 0 为中心的，这在一定程度上有助于缓解梯度更新时的一些问题，使训练过程可能更稳定一些。不过，它依然存在梯度消失的问题，常用于一些对输出值范围有相应要求且需要以 0 为中心的场景，比如在循环神经网络（RNN）的某些隐藏层中会被使用。

3.3 ReLU 函数（修正线性单元）

当输入 $x$ 大于等于 0 时，输出就是 $x$ 本身；当 $x$ 小于 0 时，输出为 0 。图像看起来是一个在 $x$ 轴负半轴为 0 ，正半轴为一条直线的折线形状。其表达式为：
$$ReLU(x)=max(0,x)$$
导数公式：
$${\text{ReLU}}^{\prime }(x)=\{\begin{array}{ll}1,& \text{if }x>0\\ 0,& \text{if }x\le 0\end{array}$$

ReLU 函数的计算非常简单，大大加快了网络的训练速度，并且在一定程度上缓解了梯度消失问题（只要输入大于 0 ，导数恒为 1 ）。不过它也有缺点，比如当输入小于 0 时，神经元处于 “死亡” 状态（永远不会被激活，导致相应权重无法更新）。目前，它是深度学习中应用非常广泛的激活函数，在很多卷积神经网络（CNN）的隐藏层等位置常常被使用。

3.4 Leaky ReLU 函数

图像与 ReLU 类似，但在 $x$ 轴负半轴不是完全为 0 ，而是有一个斜率为 $\alpha$ 的直线段。 $\alpha$ 是一个很小的常数（通常取值在（通常在 $0<\alpha <1$ ） ，常用的值在 0.01 左右）。其数学公式为：

$$LeakyReLU(x)=\{\begin{array}{ll}x,& \text{if }x\ge 0\\ \alpha x,& \text{if }x<0\end{array}$$

导数公式：
$${\text{Leaky ReLU}}^{\prime }(x)=\{\begin{array}{ll}1,& \text{if }x>0\\ \alpha ,& \text{if }x\le 0\end{array}$$
它是为了克服 ReLU 函数中神经元 “死亡” 的问题而提出的，使得在 $x$ 小于 0 时也能有一定的梯度进行反向传播，权重可以继续更新，在一些对网络鲁棒性要求较高的场景中会被选用。

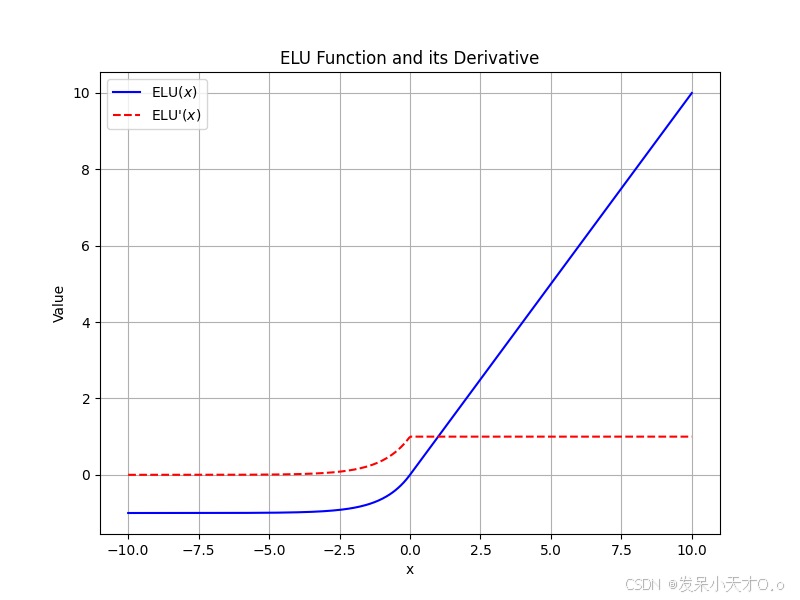
3.4 ELU 函数（指数线性单元）

在 $x$ 小于 0 时呈现出指数增长的曲线形状，在 $x$ 大于等于 0 时为直线。其中 $\alpha$ 是一个常数（常取值在 1 左右）。其数学公式如下：
$$\text{ELU}(x)=\{\begin{array}{ll}x,& \text{if }x>0\\ \alpha (\exp (x)-1),& \text{if }x\le 0\end{array}$$

导数公式：
$${\text{ELU}}^{\prime }(x)=\{\begin{array}{ll}1,& \text{if }x>0\\ \alpha \exp (x),& \text{if }x\le 0\end{array}$$

它结合了 ReLU 函数的优点，同时解决了 ReLU 中神经元 “死亡” 以及输出均值不为 0 等部分问题，在训练过程中能使网络收敛得更快、更稳定，常用于一些图像分类、自然语言处理等任务的网络结构中。