前言:本节使用霍夫变换进行直线检测,使用最小二乘法拟合直线。
1 直线检测
直线检测是图像处理中一种常见的任务,旨在从图像中提取出直线。这在许多应用中都很有用,例如道路检测、建筑物轮廓提取、对象检测等。
1.1 霍夫变换
霍夫变换(Hough Transform)是一种经典的计算机视觉算法,主要用于从图像中检测出具有特定形状的几何对象,比如直线、圆形、椭圆等。它通过将图像空间中的点映射到参数空间(也叫霍夫空间),然后通过统计这些点在参数空间中的“投票”结果来找到图像中的几何形状。最常见的是用来检测直线和圆。即使几何形状不完整或被噪声干扰。
图像空间(笛卡尔坐标): 这是原始图像的空间,每个点的位置用像素坐标 (𝑥,𝑦) 表示。
参数空间(极坐标空间): 这是一个抽象的空间,用来描述图像中几何形状的所有可能参数。例如,对于直线来说,通常我们使用极坐标(𝜌,𝜃)来描述每一条直线。
1.1.1 原理
假设在图像空间中有一个直线的表达式为:
y
=
k
x
+
b
y=kx+b
y=kx+b
其中,𝑘为斜率,𝑏为截距。但这种表示在 𝑘接近无穷大时会出现不稳定情况。为了避免这种情况,通常使用极坐标来表示直线:
ρ
=
x
c
o
s
θ
+
y
s
i
n
θ
ρ=xcosθ+ysinθ
ρ=xcosθ+ysinθ
其中,𝜌表示直线到图像坐标系原点的垂直距离,𝜃表示该垂线与x轴的夹角。这样,每条直线可以唯一地表示为 (𝜌,𝜃)。

在霍夫变换中,图像中的每一个边缘点 ( x , y ) (x,y) (x,y)都会映射到参数空间中的一条曲线。每个边缘点在参数空间中的曲线代表图像空间中所有可能通过该点的直线。曲线上的每一个点都表示一条经过 ( x , y ) (x, y) (x,y)点的直线。假设你有一个图像中的边缘点 ( x , y ) (x,y) (x,y),通过该点的每条直线都有不同的𝜌和𝜃值(不同的距离和角度),在参数空间中,该点会映射到一系列 ( ρ , θ ) (ρ, θ) (ρ,θ)值,形成一条曲线。每对 ( ρ , θ ) (ρ, θ) (ρ,θ)值表示一条直线。
如果多个图像中的边缘点(例如 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)、 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)等)对应的直线具有相同的𝜌和𝜃值,或者说它们的曲线在参数空间中交汇,那么这些边缘点所对应的直线就会在参数空间中有较高的投票(或者累积计数)。当参数空间中某个位置的投票数很高时,这就意味着有多条边缘点的曲线在该位置交汇,表示图像中存在一条实际的直线。
1.1.2 过程步骤
- 灰度图:首先将彩色图像转化为灰度图像。
- 二值化:应用阈值化操作将图像转换为二值图。
- 边缘检测: 对灰度图或二值图使用Canny边缘检测或Sobel算子进行边缘检测,获取边缘点。
- 坐标转换: 将图像中的每个边缘点根据 ρ = x c o s θ + y s i n θ ρ=xcosθ+ysinθ ρ=xcosθ+ysinθ计算其在参数空间的所有可能的 ( ρ , θ ) (ρ, θ) (ρ,θ)值,使得每个点在极坐标空间表示为一条曲线。
- 投票累积:在参数空间内创建一个二维数组(霍夫累积器),用于记录每个 ( ρ , θ ) (ρ, θ) (ρ,θ)对应的投票次数。每个边缘点的每个可能的 ( ρ , θ ) (ρ, θ) (ρ,θ)都在累积器中增加计数。若多条曲线交汇在同一点 ( ρ , θ ) (ρ, θ) (ρ,θ),则说明这些点可能在图像空间中共线。交汇点越多的 ( ρ , θ ) (ρ, θ) (ρ,θ),表示该参数组合的直线越显著。
- 检测峰值:通过设定一个阈值来筛选累积器中票数较高的 ( ρ , θ ) (ρ, θ) (ρ,θ)对应的直线。阈值设置越低,检测到的直线越多;阈值设置越高,只检测到图像中的主要直线。
- 绘制直线:将参数空间中的 ( ρ , θ ) (ρ, θ) (ρ,θ)转换回图像空间,并绘制出检测到的直线。
1.1.3 Python代码实现
在OpenCV中,霍夫变换可以通过两种方法来实现直线检测:
- 标准霍夫变换:使用 cv2.HoughLines()。
- 概率霍夫变换:使用 cv2.HoughLinesP()。
- 标准霍夫变换 (cv2.HoughLines)
该函数返回一个二维数组,每个元素是检测到的一条直线的参数 ( ρ , θ ) (ρ, θ) (ρ,θ)。即每条直线在极坐标系中的表示。
lines=cv2.HoughLines(image, rho, theta, threshold)
参数:
- image: 输入图像,必须是单通道的二值图像(通常是经过边缘检测的结果)。例如,经过 Canny 边缘检测处理的图像。
- rho: 直线距离分辨率,通常设置为 1 像素。它表示在参数空间中每个累积器单元的大小(𝜌的步长)。较大的值会减少检测到的直线数量,但可能提高计算效率。
- theta: 角度分辨率,通常设置为𝜋/180或 1 度。它表示在参数空间中每个累积器单元的角度步长。较小的值将提高检测精度,但增加计算复杂度。
- threshold: 累积器阈值。只有当累积器中的值大于这个阈值时,才会认为有一条直线存在。这是霍夫变换中的投票机制,用于选择最明显的直线。如果值太小,可能会检测到噪声。如果值太大,可能会错过一些边缘。
- 概率霍夫变换 (cv2.HoughLinesP)
cv2.HoughLinesP() 是标准霍夫变换的改进版,它可以直接返回直线的两个端点,而不是 ( ρ , θ ) (ρ, θ) (ρ,θ) 参数。这种方法更高效,也更适合在图像较大的情况下使用。
lines = cv2.HoughLinesP(image, rho, theta, threshold, minLineLength, maxLineGap)
- minLineLength:直线的最小长度,小于该值的直线将被忽略。
- maxLineGap:同一直线点之间允许的最大间隔,如果间隔小于该值,认为在同一直线上。
返回值 lines 是一个包含检测到的直线段的列表,每个直线段由四个坐标值组成:(x1, y1, x2, y2),分别表示线段的起点和终点。
import cv2
import numpy as np
image = cv2.imread("../2.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 使用Canny边缘检测
canny = cv2.Canny(gray, 150, 180)
# 使用Hough变换检测直线
lines = cv2.HoughLines(canny, 1, np.pi / 180, 123)
if lines is not None:
for line in lines:
rho, theta = line[0] # rho:直线到坐标原点的距离, theta:垂直于直线的向量与 x 轴的夹角
a = np.cos(theta) # 表示方向向量,即直线在 x 和 y 方向的分量
b = np.sin(theta)
x0 = a * rho # (x0, y0) 是直线到原点距离 rho 的位置。
y0 = b * rho # 通过 (x0, y0) 和方向向量 (a, b) 可以确定直线的两个端点
x1 = int(x0 + 1000 * (-b)) # 这里的 1000 是一个较大的常数,用来延长直线,使其可以跨越整个图像。
y1 = int(y0 + 1000 * a)
x2 = int(x0 - 1000 * (-b))
y2 = int(y0 - 1000 * a)
cv2.line(image, (x1, y1), (x2, y2), (0, 0, 255), 1)
cv2.imshow("canny", canny)
cv2.imshow("lines", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
1.1.4 C++代码实现
cv::HoughLines函数的输出参数lines,用于存储检测到的直线信息。它是一个 std::vectorcv::Vec2f 类型的容器,其中每个 cv::Vec2f 元素包含 (rho, theta) 值。
cv::HoughLinesP函数的输出参数lines,存储检测到的直线段。每条直线段用 cv::Vec4i 表示,包含 4 个整数 (x1, y1, x2, y2),表示直线的两个端点坐标。
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
cv::Mat image = cv::imread("../2.jpg");
if (image.empty())
{
std::cerr << "Could not read the image" << std::endl;
return -1;
}
cv::Mat gray;
cv::cvtColor(image, gray, cv::COLOR_BGR2GRAY);
cv::Mat edges;
cv::Canny(gray, edges, 150, 180);
std::vector<cv::Vec2f> lines;// Vec2b,(float 类型) ,二维向量, 存储检测的线条参数
cv::HoughLines(edges, lines, 1, CV_PI / 180, 123);
for (int i = 0; i < lines.size(); i++)
{
float rho = lines[i][0];
float theta = lines[i][1];
double a = cos(theta);
double b = sin(theta);
double x0 = a * rho;
double y0 = b * rho;
int x1 = cvRound(x0 + 1000 * (-b));//cvRound,四舍五入
int y1 = cvRound(y0 + 1000 * a);
int x2 = cvRound(x0 - 1000 * (-b));
int y2 = cvRound(y0 - 1000 * a);
cv::line(image, cv::Point(x1, y1), cv::Point(x2, y2), cv::Scalar(0, 0, 255), 1);
}
cv::imshow("Canny", edges);
cv::imshow("Lines", image);
cv::waitKey(0);
cv::destroyAllWindows();
return 0;
}
1.1.5 实现效果
边缘检测效果图:

直线检测效果图:

2 直线拟合
直线拟合(Line Fitting)是指根据一组数据点,通过某种算法找到一条直线,使得这条直线最能表示这些数据点的关系。在图像处理中,直线拟合常用于检测一组点中的直线或最小化某种误差(如最小二乘法)。
2.1 最小二乘法
在 OpenCV 中,最常用的直线拟合方法是最小二乘法,它是通过最小化所有数据点到直线的垂直距离的平方和来找到最佳的直线。
假设我们有一组数据点 (
x
i
,
y
i
x_i,y_i
xi,yi),通过最小化目标函数(误差的平方和),拟合出一条直线
y
=
k
x
+
b
y=kx+b
y=kx+b,其中
k
k
k是斜率,
b
b
b是截距。
目标函数:
S
(
k
,
b
)
=
∑
i
=
01
n
(
y
i
−
(
k
x
i
+
b
)
)
2
S(k,b)= \sum_{i=01}^n(y_i−(kx_i+b)) ^2
S(k,b)=i=01∑n(yi−(kxi+b))2
其中,
y
i
y_i
yi是第 i 个数据点的实际值,
k
x
i
+
b
kx_i+b
kxi+b 是拟合直线的预测值。我们需要通过调整
k
k
k和
b
b
b的值来最小化误差。
2.2 函数
在 OpenCV 中,我们可以通过 cv::fitLine 来进行最小二乘法拟合直线。该函数使用最小二乘法计算点集的最佳拟合直线,并返回直线的参数。能适用于二维和三维点集。
void cv::fitLine(
const std::vector<cv::Point2f>& points, // 输入点集
cv::Vec4f& line, // 输出直线的参数 (vx, vy, x0, y0)
int distType = cv::DIST_L2, // 距离类型,通常选择 cv::DIST_L2
double param = 0, // 参数,默认为 0
double reps = 0.01, // 精度,最小误差
double aeps = 0.01 // 相对精度
);
参数:
- points:输入的点集,通常是一个 std::vector<cv::Point2f> 或 std::vector<cv::Point3f>,二维点集每个点包含两个坐标 (x, y),三维点集每个点包含三个坐标 (x, y, z)。
- line:输出的拟合直线参数,类型为 cv::Vec4f,包含四个浮点数(vx, vy, x0, y0):直线的方向向量 (vx, vy)和直线上的一点 (x0, y0) 。或者对于 3D 点集返回 (vx, vy, vz, x0, y0, z0)。
(vx, vy) 或 (vx, vy, vz):直线的方向向量,表示直线的方向。
(x0, y0) 或 (x0, y0, z0):直线上的一个点。
- distType:距离类型,用于计算点到直线的距离。常用的有 cv::DIST_L2(欧氏距离,最常用),cv::DIST_L1(曼哈顿距离)等。
- param:距离的附加参数,通常设为 0。
- reps:表示拟合精度,即当拟合的误差小于 reps 时停止迭代。
- aeps:表示角度精度,即当角度变化小于 aeps 时停止迭代。
由于 cv::fitLine 输出的是直线的方向向量和一个点,不是直接的斜率和截距。因此,如果需要将结果转换为常用的直线方程形式
y
=
k
x
+
b
y=kx+b
y=kx+b,可以用方向向量来计算斜率 k 和截距 b:
k
=
v
y
v
x
,
b
=
y
0
−
k
⋅
x
0
k=\frac{vy}{vx},b=y0−k⋅x0
k=vxvy,b=y0−k⋅x0
方向向量可以用来在二维平面中延长直线,计算出两个端点。
使用直线的点向量方程,我们可以表示直线上任意点 (x, y) 的位置关系:
y
=
y
0
+
v
y
v
x
⋅
(
x
−
x
0
)
y=y0+ \frac{vy}{vx}⋅(x−x0)
y=y0+vxvy⋅(x−x0)
当 x = 0 时,将其代入方程求 y,得到 lefty 值:
l
e
f
t
y
=
y
0
+
v
y
v
x
⋅
(
−
x
0
)
=
y
0
−
v
y
⋅
x
0
v
x
lefty=y0+ \frac{vy}{vx}⋅(−x0)=y0− \frac{vy⋅x0}{vx}
lefty=y0+vxvy⋅(−x0)=y0−vxvy⋅x0
当 x 达到点集中最大值时,将其代入方程求 y,得到 righty 值:
r
i
g
h
t
y
=
y
0
+
v
y
v
x
⋅
(
x
m
a
x
−
x
0
)
righty=y0+ \frac{vy}{vx}⋅(x_{max}−x0)
righty=y0+vxvy⋅(xmax−x0)
2.3 Python代码实现
import cv2
import numpy as np
points = np.array([[50, 100], [200, 250], [300, 340], [400, 420], [500, 500]], dtype=np.float32)
points = points.reshape(-1, 1, 2) # 将点的形状调整为 (n, 1, 2)
# 使用 fitLine 拟合直线
line = cv2.fitLine(points, cv2.DIST_L2, 0, 0.01, 0.01)
# 解析拟合结果
vx, vy, x0, y0 = line[0], line[1], line[2], line[3]
# 计算拟合直线的两个端点
lefty = int(y0 - x0 * vy / vx) # 当 x = 0 时的 y 值
righty = int(y0 + (vy / vx) * (points[:, 0, 0].max() - x0)) # 当 x 为最大值时的 y 值
# 可视化
img = np.zeros((600, 600, 3), dtype=np.uint8)
cv2.line(img, (0, lefty), (int(points[:, 0, 0].max()), righty), (0, 0, 255), 2)
for point in points:
cv2.circle(img, (int(point[0][0]), int(point[0][1])), 5, (0, 255, 255), -1)
cv2.imshow("fitline", img)
cv2.waitKey(0)
cv2.destroyAllWindows()
2.4 C++代码实现
#include<iostream>
#include<opencv2/opencv.hpp>
int main()
{
std::vector<cv::Point2f> points = { cv::Point2f(50,100),
cv::Point2f(200, 250), cv::Point2f(300, 340),
cv::Point2f(400, 420), cv::Point2f(500, 500)
};
cv::Vec4f line;// 用于存储拟合的直线参数
// 使用 fitLine 函数进行直线拟合
cv::fitLine(points, line, cv::DIST_L1,0,0.01,0.01);
// 从输出的参数中解析出方向向量和直线上的一点
float vx = line[0];
float vy = line[1];
float x0 = line[2];
float y0 = line[3];
// 计算拟合直线的两个端点
int lefty = static_cast<int>(y0 - x0 * (vy / vx));// 当 x = 0 时的 y 值。static_cast 类型转换
int righty = static_cast<int>(y0 + (vy / vx) * (500 - x0));// 当 x 为最大值时的 y 值
cv::Mat img = cv::Mat::zeros(cv::Size(600, 600), CV_8SC3);
cv::line(img, cv::Point(0, lefty), cv::Point(500, righty), cv::Scalar(0, 0, 255), 2);
for (int i = 0; i < points.size(); i++)
{
cv::circle(img, points[i], 5, cv::Scalar(0, 255, 255), -1);
}
cv::imshow("fitline", img);
cv::waitKey(0);
cv::destroyAllWindows();
return 0;
}
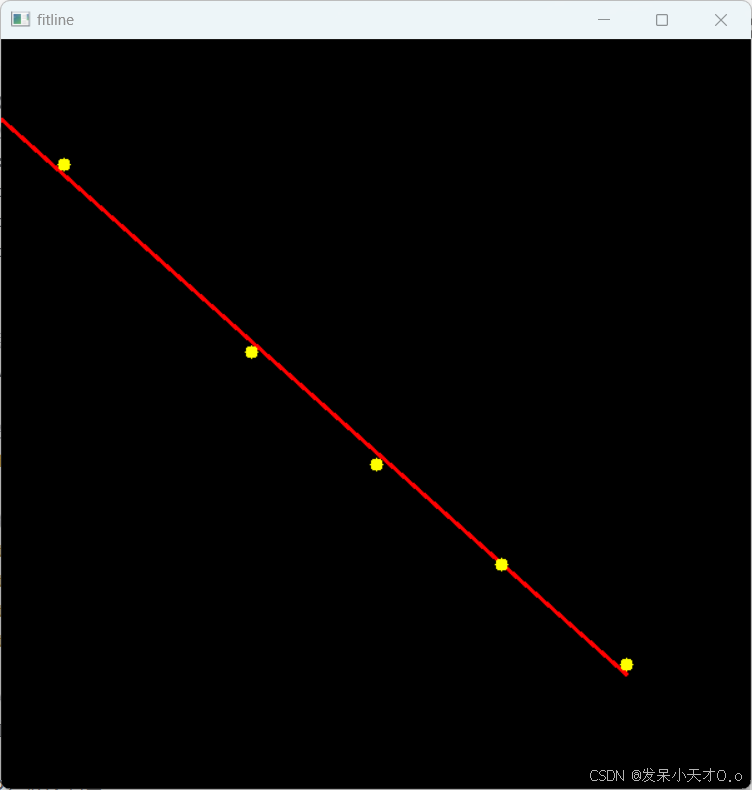
2.5 实现效果
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








