ABC213 01bfs

E

神秘建图 01bfs/dij

一个网格图，有障碍物，每次可以消除一个2*2区域里的障碍物，问要想到达右下角，最少需要消除多少次？

遇到相邻点是障碍物时，使用一次消除，有多种使用方式，如图

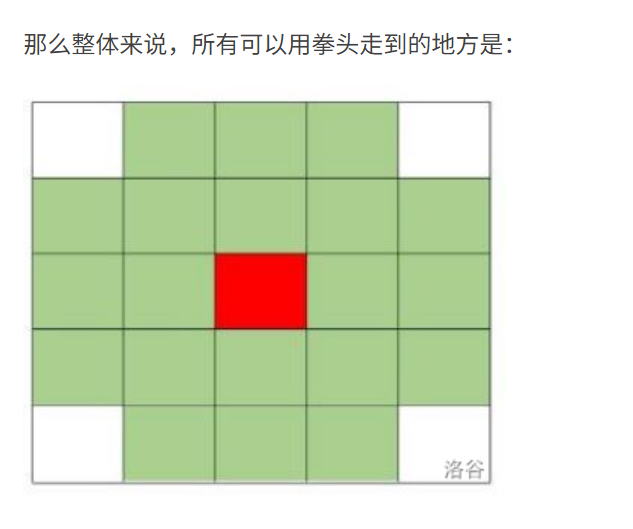
由于我们关心消除次数，这些绿的点消除次数都为1，可以看作当前点到这些绿的点有一条边权为1的边。对于直接相邻，且没有障碍物的点，边权就是0。

你可能会说，有的绿点可能没有障碍物，但是仍然被连了边权1的边？这对答案无影响，因为如果无障碍物，肯定有一个只由边权0的边组成的路径，也可以到达这个点，最小值会取这个边权0的路径。

在这张图上跑最短路即可。可以dij。但是由于边权只有01，可以用另一种更快的方法：01bfs。具体来说，仍然是个bfs+数组记录最短距离，但不用优先队列了，使用双端队列，我们可以把边权0的点松弛后放进队首，边权1的点放进队尾。

为啥这样是对的？回忆一下我们dij用优先队列的目的是什么，优先队列可以保证距离近的点先被松弛，让最短路尽可能早的被取到，从而距离更长的方案，就不会被入队，入队点数少了，复杂度就低了。而在边权只有01的图中，走0边权的边的点，肯定距离更近，我们想让他比走1边权的点先被松弛，于是把他放在队首，把1边权的放在队尾。

最后的复杂度分析，每个点最多被入队两次，复杂度$O(n)$，比dij$O(n\log n)$快很多，当然在本题时间很宽裕，两种都能通过。

实现时，需要注意，01bfs一定是根据边权01来决定是放到队首还是队尾的

dij

char a[1000][1000];
void solve(){
	int n,m;
	cin>>n>>m;
	rep(i,1,n){
		rep(j,1,m){
			cin>>a[i][j];
		}
	}
	priority_queue<array<int,3>,vector<array<int,3>>,greater<array<int,3>>>q;
	q.push({0,1,1});
	vi d(n*m+10,1e18);
	d[1]=0;
	
	while(q.size()){
		auto p=q.top();
		q.pop();
		
		int x=p[1],y=p[2],du=p[0];
		int u=(x-1)*m+y;
		if(d[u]<du)continue;
		rep(i,-2,2){
			rep(j,-2,2){
				if(i==0&&j==0)continue;
				int xx=x+i,yy=y+j;
				if(xx<1||xx>n||yy<1||yy>m)continue;
				int dis=abs(i)+abs(j);
				if(dis==4)continue;
				
				int w=1;
				if(dis==1&&a[xx][yy]=='.'){
					w=0;
				}
				int v=(xx-1)*m+yy;
				if(d[v]>d[u]+w){
					d[v]=d[u]+w;
					q.push({d[v],xx,yy});
				}
			}
		}
	}
	cout<<d[n*m];
//	rep(i,1,n){
//		rep(j,1,m){
//			cout<<d[(i-1)*m+j]<<' ';
//		}
//		cout<<'\n';
//	}
}

01bfs

char a[1000][1000];
void solve(){
	int n,m;
	cin>>n>>m;
	rep(i,1,n){
		rep(j,1,m){
			cin>>a[i][j];
		}
	}
	deque<array<int,3>>q;
	q.push_back({0,1,1});
	vi d(n*m*2,1e18);
	d[1]=0;
	
	while(q.size()){
		auto p=q.front();
		q.pop_front();
		
		int x=p[1],y=p[2],du=p[0];
		int u=(x-1)*m+y;
		if(d[u]<du)continue;
		rep(i,-2,2){
			rep(j,-2,2){
				if(i==0&&j==0)continue;
				int xx=x+i,yy=y+j;
				if(xx<1||xx>n||yy<1||yy>m)continue;
				int dis=abs(i)+abs(j);
				if(dis==4)continue;
				
				int w=1;
				if(dis==1&&a[xx][yy]=='.'){
					w=0;
				}
				int v=(xx-1)*m+yy;
				if(d[v]>d[u]+w){
					d[v]=d[u]+w;
					if(w==0)q.push_front({d[v],xx,yy});
					else q.push_back({d[v],xx,yy});
				}
			}
		}
	}
	cout<<d[n*m];
//	rep(i,1,n){
//		rep(j,1,m){
//			cout<<d[(i-1)*m+j]<<' ';
//		}
//		cout<<'\n';
//	}
}