线性方程组
1.克莱姆法则
线性方程组 { a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \begin{cases} a_{11}x_{1} + a_{12}x_{2} + \cdots +a_{1n}x_{n} = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} + \cdots + a_{2n}x_{n} =b_{2} \\ \quad\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots \\ a_{n1}x_{1} + a_{n2}x_{2} + \cdots + a_{{nn}}x_{n} = b_{n} \\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+⋯+annxn=bn,如果系数行列式 D = ∣ A ∣ ≠ 0 D = \left| A \right| \neq 0 D=∣A∣=0,则方程组有唯一解, x 1 = D 1 D , x 2 = D 2 D , ⋯ , x n = D n D x_{1} = \frac{D_{1}}{D},x_{2} = \frac{D_{2}}{D},\cdots,x_{n} =\frac{D_{n}}{D} x1=DD1,x2=DD2,⋯,xn=DDn,其中 D j D_{j} Dj是把 D D D中第 j j j列元素换成方程组右端的常数列所得的行列式。
2. n n n阶矩阵 A A A可逆 ⇔ A x = 0 \Leftrightarrow Ax = 0 ⇔Ax=0只有零解。 ⇔ ∀ b , A x = b \Leftrightarrow\forall b,Ax = b ⇔∀b,Ax=b总有唯一解,一般地, r ( A m × n ) = n ⇔ A x = 0 r(A_{m \times n}) = n \Leftrightarrow Ax= 0 r(Am×n)=n⇔Ax=0只有零解。
3.非奇次线性方程组有解的充分必要条件,线性方程组解的性质和解的结构
(1) 设 A A A为 m × n m \times n m×n矩阵,若 r ( A m × n ) = m r(A_{m \times n}) = m r(Am×n)=m,则对 A x = b Ax =b Ax=b而言必有 r ( A ) = r ( A ⋮ b ) = m r(A) = r(A \vdots b) = m r(A)=r(A⋮b)=m,从而 A x = b Ax = b Ax=b有解。
(2) 设 x 1 , x 2 , ⋯ x s x_{1},x_{2},\cdots x_{s} x1,x2,⋯xs为 A x = b Ax = b Ax=b的解,则 k 1 x 1 + k 2 x 2 ⋯ + k s x s k_{1}x_{1} + k_{2}x_{2}\cdots + k_{s}x_{s} k1x1+k2x2⋯+ksxs当 k 1 + k 2 + ⋯ + k s = 1 k_{1} + k_{2} + \cdots + k_{s} = 1 k1+k2+⋯+ks=1时仍为 A x = b Ax =b Ax=b的解;但当 k 1 + k 2 + ⋯ + k s = 0 k_{1} + k_{2} + \cdots + k_{s} = 0 k1+k2+⋯+ks=0时,则为 A x = 0 Ax =0 Ax=0的解。特别 x 1 + x 2 2 \frac{x_{1} + x_{2}}{2} 2x1+x2为 A x = b Ax = b Ax=b的解; 2 x 3 − ( x 1 + x 2 ) 2x_{3} - (x_{1} +x_{2}) 2x3−(x1+x2)为 A x = 0 Ax = 0 Ax=0的解。
(3) 非齐次线性方程组 A x = b {Ax} = b Ax=b无解 ⇔ r ( A ) + 1 = r ( A ‾ ) ⇔ b \Leftrightarrow r(A) + 1 =r(\overline{A}) \Leftrightarrow b ⇔r(A)+1=r(A)⇔b不能由 A A A的列向量 α 1 , α 2 , ⋯ , α n \alpha_{1},\alpha_{2},\cdots,\alpha_{n} α1,α2,⋯,αn线性表示。
4.奇次线性方程组的基础解系和通解,解空间,非奇次线性方程组的通解
(1) 齐次方程组 A x = 0 {Ax} = 0 Ax=0恒有解(必有零解)。当有非零解时,由于解向量的任意线性组合仍是该齐次方程组的解向量,因此 A x = 0 {Ax}= 0 Ax=0的全体解向量构成一个向量空间,称为该方程组的解空间,解空间的维数是 n − r ( A ) n - r(A) n−r(A),解空间的一组基称为齐次方程组的基础解系。
(2) η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt是 A x = 0 {Ax} = 0 Ax=0的基础解系,即:
-
η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt是 A x = 0 {Ax} = 0 Ax=0的解;
-
η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt线性无关;
-
A x = 0 {Ax} = 0 Ax=0的任一解都可以由 η 1 , η 2 , ⋯ , η t \eta_{1},\eta_{2},\cdots,\eta_{t} η1,η2,⋯,ηt线性表出.
k 1 η 1 + k 2 η 2 + ⋯ + k t η t k_{1}\eta_{1} + k_{2}\eta_{2} + \cdots + k_{t}\eta_{t} k1η1+k2η2+⋯+ktηt是 A x = 0 {Ax} = 0 Ax=0的通解,其中 k 1 , k 2 , ⋯ , k t k_{1},k_{2},\cdots,k_{t} k1,k2,⋯,kt是任意常数。
矩阵的特征值和特征向量
1.矩阵的特征值和特征向量的概念及性质
(1) 设
λ
\lambda
λ是
A
A
A的一个特征值,则
k
A
,
a
A
+
b
E
,
A
2
,
A
m
,
f
(
A
)
,
A
T
,
A
−
1
,
A
∗
{kA},{aA} + {bE},A^{2},A^{m},f(A),A^{T},A^{- 1},A^{*}
kA,aA+bE,A2,Am,f(A),AT,A−1,A∗有一个特征值分别为
k
λ
,
a
λ
+
b
,
λ
2
,
λ
m
,
f
(
λ
)
,
λ
,
λ
−
1
,
∣
A
∣
λ
,
{kλ},{aλ} + b,\lambda^{2},\lambda^{m},f(\lambda),\lambda,\lambda^{- 1},\frac{|A|}{\lambda},
kλ,aλ+b,λ2,λm,f(λ),λ,λ−1,λ∣A∣,且对应特征向量相同(
A
T
A^{T}
AT 例外)。
(2)若 λ 1 , λ 2 , ⋯ , λ n \lambda_{1},\lambda_{2},\cdots,\lambda_{n} λ1,λ2,⋯,λn为 A A A的 n n n个特征值,则 ∑ i = 1 n λ i = ∑ i = 1 n a i i , ∏ i = 1 n λ i = ∣ A ∣ \sum_{i= 1}^{n}\lambda_{i} = \sum_{i = 1}^{n}a_{{ii}},\prod_{i = 1}^{n}\lambda_{i}= |A| ∑i=1nλi=∑i=1naii,∏i=1nλi=∣A∣ ,从而 ∣ A ∣ ≠ 0 ⇔ A |A| \neq 0 \Leftrightarrow A ∣A∣=0⇔A没有特征值。
(3)设 λ 1 , λ 2 , ⋯ , λ s \lambda_{1},\lambda_{2},\cdots,\lambda_{s} λ1,λ2,⋯,λs为 A A A的 s s s个特征值,对应特征向量为 α 1 , α 2 , ⋯ , α s \alpha_{1},\alpha_{2},\cdots,\alpha_{s} α1,α2,⋯,αs,
若: α = k 1 α 1 + k 2 α 2 + ⋯ + k s α s \alpha = k_{1}\alpha_{1} + k_{2}\alpha_{2} + \cdots + k_{s}\alpha_{s} α=k1α1+k2α2+⋯+ksαs ,
则: A n α = k 1 A n α 1 + k 2 A n α 2 + ⋯ + k s A n α s = k 1 λ 1 n α 1 + k 2 λ 2 n α 2 + ⋯ k s λ s n α s A^{n}\alpha = k_{1}A^{n}\alpha_{1} + k_{2}A^{n}\alpha_{2} + \cdots +k_{s}A^{n}\alpha_{s} = k_{1}\lambda_{1}^{n}\alpha_{1} +k_{2}\lambda_{2}^{n}\alpha_{2} + \cdots k_{s}\lambda_{s}^{n}\alpha_{s} Anα=k1Anα1+k2Anα2+⋯+ksAnαs=k1λ1nα1+k2λ2nα2+⋯ksλsnαs 。
2.相似变换、相似矩阵的概念及性质
(1) 若 A ∼ B A \sim B A∼B,则
-
A T ∼ B T , A − 1 ∼ B − 1 , , A ∗ ∼ B ∗ A^{T} \sim B^{T},A^{- 1} \sim B^{- 1},,A^{*} \sim B^{*} AT∼BT,A−1∼B−1,,A∗∼B∗
-
∣ A ∣ = ∣ B ∣ , ∑ i = 1 n A i i = ∑ i = 1 n b i i , r ( A ) = r ( B ) |A| = |B|,\sum_{i = 1}^{n}A_{{ii}} = \sum_{i =1}^{n}b_{{ii}},r(A) = r(B) ∣A∣=∣B∣,∑i=1nAii=∑i=1nbii,r(A)=r(B)
-
∣ λ E − A ∣ = ∣ λ E − B ∣ |\lambda E - A| = |\lambda E - B| ∣λE−A∣=∣λE−B∣,对 ∀ λ \forall\lambda ∀λ成立
3.矩阵可相似对角化的充分必要条件
(1)设 A A A为 n n n阶方阵,则 A A A可对角化 ⇔ \Leftrightarrow ⇔对每个 k i k_{i} ki重根特征值 λ i \lambda_{i} λi,有 n − r ( λ i E − A ) = k i n-r(\lambda_{i}E - A) = k_{i} n−r(λiE−A)=ki
(2) 设 A A A可对角化,则由 P − 1 A P = Λ , P^{- 1}{AP} = \Lambda, P−1AP=Λ,有 A = P Λ P − 1 A = {PΛ}P^{-1} A=PΛP−1,从而 A n = P Λ n P − 1 A^{n} = P\Lambda^{n}P^{- 1} An=PΛnP−1
(3) 重要结论
-
若 A ∼ B , C ∼ D A \sim B,C \sim D A∼B,C∼D,则 [ A O O C ] ∼ [ B O O D ] \begin{bmatrix} A & O \\ O & C \\\end{bmatrix} \sim \begin{bmatrix} B & O \\ O & D \\\end{bmatrix} [AOOC]∼[BOOD].
-
若 A ∼ B A \sim B A∼B,则 f ( A ) ∼ f ( B ) , ∣ f ( A ) ∣ ∼ ∣ f ( B ) ∣ f(A) \sim f(B),\left| f(A) \right| \sim \left| f(B)\right| f(A)∼f(B),∣f(A)∣∼∣f(B)∣,其中 f ( A ) f(A) f(A)为关于 n n n阶方阵 A A A的多项式。
-
若 A A A为可对角化矩阵,则其非零特征值的个数(重根重复计算)=秩( A A A)
4.实对称矩阵的特征值、特征向量及相似对角阵
(1)相似矩阵:设 A , B A,B A,B为两个 n n n阶方阵,如果存在一个可逆矩阵 P P P,使得 B = P − 1 A P B =P^{- 1}{AP} B=P−1AP成立,则称矩阵 A A A与 B B B相似,记为 A ∼ B A \sim B A∼B。
(2)相似矩阵的性质:如果 A ∼ B A \sim B A∼B则有:
-
A T ∼ B T A^{T} \sim B^{T} AT∼BT
-
A − 1 ∼ B − 1 A^{- 1} \sim B^{- 1} A−1∼B−1 (若 A A A, B B B均可逆)
-
A k ∼ B k A^{k} \sim B^{k} Ak∼Bk ( k k k为正整数)
-
∣ λ E − A ∣ = ∣ λ E − B ∣ \left| {λE} - A \right| = \left| {λE} - B \right| ∣λE−A∣=∣λE−B∣,从而 A , B A,B A,B
有相同的特征值 -
∣ A ∣ = ∣ B ∣ \left| A \right| = \left| B \right| ∣A∣=∣B∣,从而 A , B A,B A,B同时可逆或者不可逆
-
秩 ( A ) = \left( A \right) = (A)=秩 ( B ) , ∣ λ E − A ∣ = ∣ λ E − B ∣ \left( B \right),\left| {λE} - A \right| =\left| {λE} - B \right| (B),∣λE−A∣=∣λE−B∣, A , B A,B A,B不一定相似
二次型
1. n \mathbf{n} n个变量 x 1 , x 2 , ⋯ , x n \mathbf{x}_{\mathbf{1}}\mathbf{,}\mathbf{x}_{\mathbf{2}}\mathbf{,\cdots,}\mathbf{x}_{\mathbf{n}} x1,x2,⋯,xn的二次齐次函数
f ( x 1 , x 2 , ⋯ , x n ) = ∑ i = 1 n ∑ j = 1 n a i j x i y j f(x_{1},x_{2},\cdots,x_{n}) = \sum_{i = 1}^{n}{\sum_{j =1}^{n}{a_{{ij}}x_{i}y_{j}}} f(x1,x2,⋯,xn)=∑i=1n∑j=1naijxiyj,其中 a i j = a j i ( i , j = 1 , 2 , ⋯ , n ) a_{{ij}} = a_{{ji}}(i,j =1,2,\cdots,n) aij=aji(i,j=1,2,⋯,n),称为 n n n元二次型,简称二次型. 若令 x = [ x 1 x 1 ⋮ x n ] , A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ] x = \ \begin{bmatrix}x_{1} \\ x_{1} \\ \vdots \\ x_{n} \\ \end{bmatrix},A = \begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \cdots &\cdots &\cdots &\cdots \\ a_{n1}& a_{n2} & \cdots & a_{{nn}} \\\end{bmatrix} x= x1x1⋮xn ,A= a11a21⋯an1a12a22⋯an2⋯⋯⋯⋯a1na2n⋯ann ,这二次型 f f f可改写成矩阵向量形式 f = x T A x f =x^{T}{Ax} f=xTAx。其中 A A A称为二次型矩阵,因为 a i j = a j i ( i , j = 1 , 2 , ⋯ , n ) a_{{ij}} =a_{{ji}}(i,j =1,2,\cdots,n) aij=aji(i,j=1,2,⋯,n),所以二次型矩阵均为对称矩阵,且二次型与对称矩阵一一对应,并把矩阵 A A A的秩称为二次型的秩。
2.惯性定理,二次型的标准形和规范形
(1) 惯性定理
对于任一二次型,不论选取怎样的合同变换使它化为仅含平方项的标准型,其正负惯性指数与所选变换无关,这就是所谓的惯性定理。
(2) 标准形
二次型 f = ( x 1 , x 2 , ⋯ , x n ) = x T A x f = \left( x_{1},x_{2},\cdots,x_{n} \right) =x^{T}{Ax} f=(x1,x2,⋯,xn)=xTAx经过合同变换 x = C y x = {Cy} x=Cy化为 f = x T A x = y T C T A C f = x^{T}{Ax} =y^{T}C^{T}{AC} f=xTAx=yTCTAC
y = ∑ i = 1 r d i y i 2 y = \sum_{i = 1}^{r}{d_{i}y_{i}^{2}} y=∑i=1rdiyi2称为 f ( r ≤ n ) f(r \leq n) f(r≤n)的标准形。在一般的数域内,二次型的标准形不是唯一的,与所作的合同变换有关,但系数不为零的平方项的个数由 r ( A ) r(A) r(A)唯一确定。
(3) 规范形
任一实二次型 f f f都可经过合同变换化为规范形 f = z 1 2 + z 2 2 + ⋯ z p 2 − z p + 1 2 − ⋯ − z r 2 f = z_{1}^{2} + z_{2}^{2} + \cdots z_{p}^{2} - z_{p + 1}^{2} - \cdots -z_{r}^{2} f=z12+z22+⋯zp2−zp+12−⋯−zr2,其中 r r r为 A A A的秩, p p p为正惯性指数, r − p r -p r−p为负惯性指数,且规范型唯一。
3.用正交变换和配方法化二次型为标准形,二次型及其矩阵的正定性
设 A A A正定 ⇒ k A ( k > 0 ) , A T , A − 1 , A ∗ \Rightarrow {kA}(k > 0),A^{T},A^{- 1},A^{*} ⇒kA(k>0),AT,A−1,A∗正定; ∣ A ∣ > 0 |A| >0 ∣A∣>0, A A A可逆; a i i > 0 a_{{ii}} > 0 aii>0,且 ∣ A i i ∣ > 0 |A_{{ii}}| > 0 ∣Aii∣>0
A A A, B B B正定 ⇒ A + B \Rightarrow A +B ⇒A+B正定,但 A B {AB} AB, B A {BA} BA不一定正定
A A A正定 ⇔ f ( x ) = x T A x > 0 , ∀ x ≠ 0 \Leftrightarrow f(x) = x^{T}{Ax} > 0,\forall x \neq 0 ⇔f(x)=xTAx>0,∀x=0
⇔ A \Leftrightarrow A ⇔A的各阶顺序主子式全大于零
⇔ A \Leftrightarrow A ⇔A的所有特征值大于零
⇔ A \Leftrightarrow A ⇔A的正惯性指数为 n n n
⇔ \Leftrightarrow ⇔存在可逆阵 P P P使 A = P T P A = P^{T}P A=PTP
⇔ \Leftrightarrow ⇔存在正交矩阵 Q Q Q,使 Q T A Q = Q − 1 A Q = ( λ 1 ⋱ λ n ) , Q^{T}{AQ} = Q^{- 1}{AQ} =\begin{pmatrix} \lambda_{1} & & \\ \begin{matrix} & \\ & \\ \end{matrix} &\ddots & \\ & & \lambda_{n} \\ \end{pmatrix}, QTAQ=Q−1AQ= λ1⋱λn ,
其中 λ i > 0 , i = 1 , 2 , ⋯ , n . \lambda_{i} > 0,i = 1,2,\cdots,n. λi>0,i=1,2,⋯,n.正定 ⇒ k A ( k > 0 ) , A T , A − 1 , A ∗ \Rightarrow {kA}(k >0),A^{T},A^{- 1},A^{*} ⇒kA(k>0),AT,A−1,A∗正定; ∣ A ∣ > 0 , A |A| > 0,A ∣A∣>0,A可逆; a i i > 0 a_{{ii}} >0 aii>0,且 ∣ A i i ∣ > 0 |A_{{ii}}| > 0 ∣Aii∣>0 。
奇异值分解(SVD)
参考文章:SVD原理总结
奇异值分解(SVD)在降维,数据压缩,推荐系统等有广泛的应用,任何矩阵都可以进行奇异值分解。下面通过正交变换不改变基向量间的夹角循序渐进的推导SVD算法,以及用协方差含义去理解行降维和列降维,最后介绍了SVD的数据压缩原理 。
1.正交变化
X = U Y X=UY X=UY
上式表示:X是Y的正交变换 ,其中U是正交矩阵,X和Y为列向量 。
正交变换的含义:
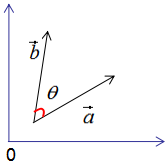
假设有两个单位列向量 a ⃗ , b ⃗ \vec{a},\vec{b} a,b,两向量的夹角为 θ θ θ,如图:
对向量
a
⃗
,
b
⃗
\vec{a},\vec{b}
a,b进行正交变换:
a
′
⃗
=
U
∗
a
⃗
b
′
⃗
=
U
∗
b
⃗
\vec{a^{'}}=U*\vec{a} \qquad \vec{b^{'}}=U*\vec{b}
a′=U∗ab′=U∗b
a
′
⃗
,
b
′
⃗
\vec{a^{'}},\vec{b^{'}}
a′,b′的模(正交变换不改变向量的模)【
∣
∣
x
∣
∣
||x||
∣∣x∣∣表示范数,也有距离、长度的概念】:
∣
∣
a
′
⃗
∣
∣
=
∣
∣
U
∗
a
⃗
∣
∣
=
∣
∣
U
∣
∣
∗
∣
∣
a
⃗
∣
∣
=
∣
∣
a
⃗
∣
∣
=
1
∣
∣
b
′
⃗
∣
∣
=
∣
∣
U
∗
b
⃗
∣
∣
=
∣
∣
U
∣
∣
∗
∣
∣
b
⃗
∣
∣
=
∣
∣
b
⃗
∣
∣
=
1
||\vec{a^{'}}||=||U*\vec{a}||=||U||*||\vec{a}||=||\vec{a}||=1\\ ||\vec{b^{'}}||=||U*\vec{b}||=||U||*||\vec{b}||=||\vec{b}||=1
∣∣a′∣∣=∣∣U∗a∣∣=∣∣U∣∣∗∣∣a∣∣=∣∣a∣∣=1∣∣b′∣∣=∣∣U∗b∣∣=∣∣U∣∣∗∣∣b∣∣=∣∣b∣∣=1
a
′
⃗
,
b
′
⃗
\vec{a^{'}},\vec{b^{'}}
a′,b′的内积(正交变换前后的内积相等):
a
′
⃗
T
∗
b
′
⃗
=
(
U
∗
a
⃗
)
T
(
U
∗
b
⃗
)
=
a
⃗
T
U
T
U
b
⃗
=
a
⃗
T
b
⃗
\vec{a^{'}}^T*\vec{b^{'}}=(U*\vec{a})^{T}(U*\vec{b})=\vec{a}^{T}U^{T}U\vec{b}=\vec{a}^{T}\vec{b}
a′T∗b′=(U∗a)T(U∗b)=aTUTUb=aTb
a
′
⃗
,
b
′
⃗
\vec{a^{'}},\vec{b^{'}}
a′,b′的夹角
θ
′
\theta^{'}
θ′(由上面的公式可得
θ
=
θ
′
\theta=\theta^{'}
θ=θ′):
c
o
s
θ
=
a
⃗
T
∗
b
⃗
∣
a
⃗
∣
∣
b
⃗
∣
c
o
s
θ
′
=
a
′
⃗
T
∗
b
′
⃗
∣
a
′
⃗
∣
∣
b
′
⃗
∣
cos\theta=\frac{\vec{a}^T*\vec{b}}{|\vec{a}||\vec{b}|} \qquad cos\theta^{'}=\frac{\vec{a^{'}}^T*\vec{b^{'}}}{|\vec{a^{'}}||\vec{b^{'}}|}
cosθ=∣a∣∣b∣aT∗bcosθ′=∣a′∣∣b′∣a′T∗b′
因此,正交变换的性质可用下图来表示:
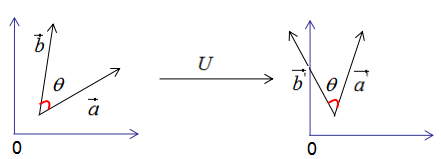
正交变换的两个重要性质:
- 正交变换不改变向量的模。
- 正交变换不改变向量的夹角。
如果向量 a ⃗ , b ⃗ \vec{a},\vec{b} a,b是基向量,那么正交变换后的结果如下:
向量空间的基是它的一个特殊的子集,基的元素称为基向量。向量空间中任意一个元素,都可以唯一地表示成基向量的线性组合。基向量之间是线性无关的。
例子:考虑所有坐标 (a,b)的向量空间R,这里的a和b都是实数。则非常自然和简单的基就是向量 e 1 = ( 1 , 0 ) e_1= (1,0) e1=(1,0)和 e 2 = ( 0 , 1 ) e_2=(0,1) e2=(0,1):假设v= (a,b)是R中的向量,则 v = a ( 1 , 0 ) + b ( 0 , 1 ) v=a(1,0)+b(0,1) v=a(1,0)+b(0,1)。而任何两个线性无关向量如 (1,1)和(−1,2),也形成R的一个基。
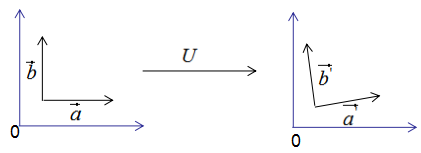
上图可以得到重要结论:基向量正交变换后的结果仍是基向量 。基向量是表示向量最简洁的方法,向量在基向量的投影就是所在基向量的坐标,我们通过这种思想去理解特征值分解和推导SVD分解。
为什么要正交变换?
正交变换图形上最直观的作用是:一巴掌把歪七扭八的图形打正,如下:

图形立正的同时,不改变其大小与形状,表达式也随之“标准化”【规范型系数只有1,0,-1】, x i x j x_ix_j xixj杂项群魔退散,平方项真身显现。
例题:求椭圆 2 x 2 + 4 x y + 5 y 2 = 1 2x^2+4xy+5y^2=1 2x2+4xy+5y2=1的面积
上式改写成矩阵形式: X T [ 2 2 2 5 ] X = 1 X^T\begin{bmatrix} 2 & 2 \\ 2 & 5 \end{bmatrix}X=1 XT[2225]X=1
①求特征值和特征向量
∣ λ E − A ∣ = 0 ⇒ λ 1 = 6 , λ 2 = 1 ( λ i E − A ) α ⇒ α 1 = ( 1 , 2 ) T , α 2 = ( − 2 , 1 ) T |\lambda{E}-A|=0\Rightarrow\lambda_1=6,\lambda_2=1\\ (\lambda_i{E}-A)\alpha\Rightarrow\alpha_1=(1,2)^T,\alpha_2=(-2,1)^T ∣λE−A∣=0⇒λ1=6,λ2=1(λiE−A)α⇒α1=(1,2)T,α2=(−2,1)T
②特征向量正交化(未正交需要施密特正交化)、单位化单位化: α 1 ′ = α 1 ∣ α 1 ∣ , α 2 ′ = α 2 ∣ α 2 ∣ \alpha_{1}^{'}=\frac{\alpha_1}{|\alpha_1|},\alpha_{2}^{'}=\frac{\alpha_2}{|\alpha_2|} α1′=∣α1∣α1,α2′=∣α2∣α2;正交矩阵为: Q = ( a 1 ′ , a 2 ′ ) Q=(a_{1}^{'},a_{2}^{'}) Q=(a1′,a2′)
③化为标准型
f = X T A X f=X^TAX f=XTAX在 X = Q Y X=QY X=QY的作用下,化为 f = y T Q T A Q y = 6 y 1 2 + y 2 2 f=y^{T}Q^{T}AQy=6y_1^2+y_2^2 f=yTQTAQy=6y12+y22.
最后由面积公式 S = π a b S=\pi{a}b S=πab求得面积。
2.特征值分解的含义
对称方阵A的特征值分解为: A = U Σ U − 1 A=U\Sigma{U^{-1}} A=UΣU−1,其中 U U U是正交矩阵, Σ \Sigma Σ是由方阵A得特征值构成得对角矩阵(奇异矩阵)。
为了可视化特征值分解,假设A是2×2的对称矩阵,
U
=
(
u
1
,
u
2
)
,
Σ
=
(
λ
1
,
λ
2
)
U=(u_1,u_2),\Sigma=(\lambda_1,\lambda_2)
U=(u1,u2),Σ=(λ1,λ2),则将上式展开为:
A
u
1
=
λ
1
u
1
A
u
2
=
λ
2
u
2
Au_1=\lambda_1u_1 \qquad Au_2=\lambda_2u_2
Au1=λ1u1Au2=λ2u2
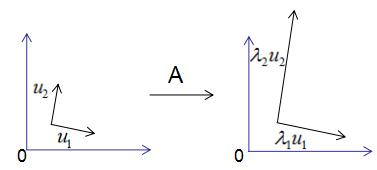
由上图可知,矩阵A没有旋转特征向量,它只是对特征向量进行了拉伸或缩短(取决于特征值的大小),因此,对称矩阵对其特征向量(基向量)的变换仍然是基向量(单位化) 。
**特征向量和特征值的几何意义:**若向量经过矩阵变换后保持方向不变,只是进行长度上的伸缩,那么该向量是矩阵的特征向量,伸缩倍数是特征值。
3.SVD分解推导
我们考虑了当基向量是对称矩阵的特征向量时,矩阵变换后仍是基向量,但是,我们在实际项目中遇到的大都是行和列不相等的矩阵,如统计每个学生的科目乘积,行数为学生个数,列数为科目数,这种形成的矩阵很难是方阵,因此SVD分解是更普遍的矩阵分解方法 。
回顾一下正交变换的思想:基向量正交变换后的结果仍是基向量 。
用正交变换的思想来推导SVD分解:
假设矩阵
A
M
×
N
A_{M\times{N}}
AM×N,秩为
K
K
K,
R
a
n
k
(
A
)
=
k
Rank(A)=k
Rank(A)=k。存在一组正交基
V
V
V:
V
=
(
v
1
,
v
2
,
…
,
v
k
)
V=(v_1,v_2,\dots,v_k)
V=(v1,v2,…,vk)
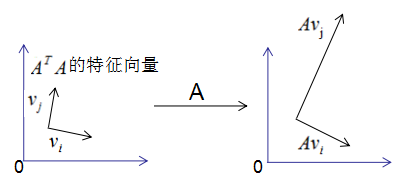
矩阵对其变换后仍是正交基,记为
U
U
U:
U
=
(
A
v
1
,
A
v
2
,
…
,
A
v
k
)
U=(Av_1,Av_2,\dots,Av_k)
U=(Av1,Av2,…,Avk)
由正交基定义,得:
(
A
v
i
)
T
(
A
v
j
)
=
0
(Av_i)^T(Av_j)=0
(Avi)T(Avj)=0,将其展开有:
v
i
T
A
T
A
v
j
=
0
w
h
e
n
v
i
i
s
t
h
e
e
i
g
e
n
v
e
c
t
o
r
o
f
A
T
A
:
(
A
T
A
)
v
i
=
λ
v
i
t
h
e
f
o
r
m
u
l
a
a
b
o
v
e
c
o
n
v
e
r
t
t
o
:
λ
v
i
T
v
j
=
0
v_{i}^{T}A^TAv_j=0\\ when\;v_i\;is\;the\;eigenvector\;of\;A^TA:(A^TA)v_i=\lambda{v_i}\\ the\;formula\;above\;convert\;to:\lambda{v_{i}^T}v_j=0
viTATAvj=0whenviistheeigenvectorofATA:(ATA)vi=λvitheformulaaboveconvertto:λviTvj=0
假设成立。
正交向量的模:
∣
∣
A
v
i
∣
∣
2
=
(
A
v
i
)
T
(
A
v
i
)
⇒
v
i
T
A
T
A
v
i
⇒
λ
i
v
i
T
v
i
=
λ
i
∴
∣
∣
A
v
i
∣
∣
=
λ
i
||Av_i||^2=(Av_i)^T(Av_i)\Rightarrow\;v_{i}^{T}A^TAv_i\Rightarrow\;\lambda_{i}v_{i}^{T}v_i=\lambda_i\\ \therefore||Av_i||=\sqrt{\lambda_i}
∣∣Avi∣∣2=(Avi)T(Avi)⇒viTATAvi⇒λiviTvi=λi∴∣∣Avi∣∣=λi
单位化正交向量,得:
u
i
=
A
v
i
∣
∣
A
v
i
∣
∣
=
1
λ
i
A
v
i
∴
A
v
i
=
λ
i
∗
u
i
u_i=\frac{Av_i}{||Av_i||}=\frac{1}{\sqrt{\lambda_i}}Av_i\\ \therefore\;Av_i=\sqrt{\lambda_i}*u_i
ui=∣∣Avi∣∣Avi=λi1Avi∴Avi=λi∗ui
结论:当基向量是
A
T
A
A^TA
ATA的特征向量时,矩阵A转换后的向量也是基向量 。
用矩阵表示上式: A V = U Σ AV=U\Sigma AV=UΣ
其中 V = ( v 1 , v 2 , … , v k ) , Σ = [ σ 1 σ 2 ⋱ σ k ] , U = ( u 1 , u 2 , … , u k ) , σ i = λ i V=(v_1,v_2,\dots,v_k),\Sigma=\begin{bmatrix}\sigma_1&&&&\\&\sigma_2\\&&\ddots\\&&&\sigma_k\end{bmatrix},U=(u_1,u_2,\dots,u_k),\sigma_i=\sqrt{\lambda_i} V=(v1,v2,…,vk),Σ= σ1σ2⋱σk ,U=(u1,u2,…,uk),σi=λi.
矩阵 V N × K , U M × K , Σ M × K V_{N\times{K}},U_{M\times{K}},\Sigma_{M\times{K}} VN×K,UM×K,ΣM×K需要扩展成方阵:
将正交基 U = ( u 1 , u 2 , … , u k ) U=(u_1,u_2,\dots,u_k) U=(u1,u2,…,uk)扩展成 ( u 1 , u 2 , … , u n ) R n (u_1,u_2,\dots,u_n)R^{n} (u1,u2,…,un)Rn空间的正交基,即方阵 U N × N U_{N\times{N}} UN×N.
将正交基 V = ( v 1 , v 2 , … , v k ) V=(v_1,v_2,\dots,v_k) V=(v1,v2,…,vk)扩展成 ( v 1 , v 2 , … , v n ) R n (v_1,v_2,\dots,v_n)R^{n} (v1,v2,…,vn)Rn空间的正交基,即方阵 V N × N V_{N\times{N}} VN×N,其中 ( v k + 1 , v k + 2 , … , v n ) (v_{k+1},v_{k+2},\dots,v_n) (vk+1,vk+2,…,vn)是矩阵A的零空间,即: A v i = 0 , i > k Av_i=0,i>k Avi=0,i>k,对应特征值 σ i = 0 \sigma_i=0 σi=0.
因此矩阵表示的式子转换为向量形式:
A
V
=
U
Σ
⇒
A
(
v
i
,
v
2
…
,
v
k
∣
v
k
+
1
,
v
k
+
2
,
…
,
v
n
)
=
(
u
i
,
u
2
…
,
u
k
∣
u
k
+
1
,
u
k
+
2
,
…
,
u
n
)
[
σ
1
σ
2
⋱
σ
k
0
⋱
0
]
AV=U\Sigma\Rightarrow\\ A(v_i,v_2\dots,v_k|v_{k+1},v_{k+2},\dots,v_n)=(u_i,u_2\dots,u_k|u_{k+1},u_{k+2},\dots,u_n) \begin{bmatrix} \sigma_1&&&&&&\\&\sigma_2&&&&&\\&&\ddots&&&&\\&&&\sigma_k&&&\\&&&&0&&\\&&&&&\ddots&\\&&&&&&0 \end{bmatrix}
AV=UΣ⇒A(vi,v2…,vk∣vk+1,vk+2,…,vn)=(ui,u2…,uk∣uk+1,uk+2,…,un)
σ1σ2⋱σk0⋱0
两式右乘
V
T
V^T
VT,可得矩阵的奇异值分解:
A
=
U
Σ
V
T
=
(
u
i
,
u
2
…
,
u
k
∣
u
k
+
1
,
u
k
+
2
,
…
,
u
n
)
[
σ
1
σ
2
⋱
σ
k
0
⋱
0
]
[
v
1
T
⋮
v
k
T
v
k
+
1
T
⋮
v
n
T
]
=
(
u
i
,
u
2
…
,
u
k
)
[
σ
1
σ
2
⋱
σ
k
]
[
v
1
T
⋮
v
k
T
]
令:
X
=
(
u
i
,
u
2
…
,
u
k
)
[
σ
1
σ
2
⋱
σ
k
]
=
(
σ
1
u
1
,
σ
2
u
2
,
…
,
σ
k
u
k
)
Y
=
[
v
1
T
⋮
v
k
T
]
则:
A
=
X
Y
A=U\Sigma{V^T}\\ =(u_i,u_2\dots,u_k|u_{k+1},u_{k+2},\dots,u_n) \begin{bmatrix} \sigma_1&&&&&&\\&\sigma_2&&&&&\\&&\ddots&&&&\\&&&\sigma_k&&&\\&&&&0&&\\&&&&&\ddots&\\&&&&&&0 \end{bmatrix} \begin{bmatrix} v_1^T\\ \vdots\\v_k^T\\v_{k+1}^T\\ \vdots\\v_n^T \end{bmatrix}\\ =(u_i,u_2\dots,u_k) \begin{bmatrix} \sigma_1&&&\\&\sigma_2&&\\&&\ddots&\\&&&\sigma_k \end{bmatrix} \begin{bmatrix} v_1^T\\ \vdots\\v_k^T \end{bmatrix}\\ 令:X=(u_i,u_2\dots,u_k) \begin{bmatrix} \sigma_1&&&\\&\sigma_2&&\\&&\ddots&\\&&&\sigma_k \end{bmatrix}=(\sigma_1u_1,\sigma_2u_2,\dots,\sigma_ku_k)\\ Y=\begin{bmatrix} v_1^T\\ \vdots\\v_k^T \end{bmatrix}\\ 则:A=XY
A=UΣVT=(ui,u2…,uk∣uk+1,uk+2,…,un)
σ1σ2⋱σk0⋱0
v1T⋮vkTvk+1T⋮vnT
=(ui,u2…,uk)
σ1σ2⋱σk
v1T⋮vkT
令:X=(ui,u2…,uk)
σ1σ2⋱σk
=(σ1u1,σ2u2,…,σkuk)Y=
v1T⋮vkT
则:A=XY
因为X和Y分别是列满秩和行满秩,所以上式是A的满秩分解。






















 632
632











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








