c++ STL 红黑树实现

最新推荐文章于 2024-10-04 23:09:21 发布

Morphad

最新推荐文章于 2024-10-04 23:09:21 发布

阅读量2.1k

点赞数 2

分类专栏： cpp

本文链接：https://blog.csdn.net/Morphad/article/details/9799517

版权

本文探讨了红黑树的特性及其在Linux内核、nginx和C++ STL中的应用。着重分析了红黑树节点的插入和删除过程，包括插入平衡操作和删除平衡操作，涉及颜色调整和树旋转策略。

摘要由CSDN通过智能技术生成

红黑树是一种自平衡二叉查找树,它的操作有着良好的最坏情况运行时间，并且在实践中是高效的: 它可以在O(log n)时间内做查找，插入和删除，这里的n是树中元素的数目。

红黑树应用：
1.linux内核中，进程的虚拟地址区间由红黑树组织管理
2.nginx中，超时时间由红黑树组织管理
3.C++ STL中，C++中set,multiset,map,multimap集合模板类都是在STL红黑树的基础之上实现的
......

下面看红黑树在gcc中C++标准库的实现，只关注结点的插入、删除及相应的树平衡操作

I.红黑树的结点

/* gcc-4.4.5/libstdc++-v3/include/bits/stl_tree.h */
/* /usr/include/c++/4.4.4/bits/stl_tree.h */
  85   enum _Rb_tree_color { _S_red = false, _S_black = true };
  86 
  87   struct _Rb_tree_node_base
  88   {
  89     typedef _Rb_tree_node_base* _Base_ptr;
  90     typedef const _Rb_tree_node_base* _Const_Base_ptr;
  91 
  92     _Rb_tree_color      _M_color;
  93     _Base_ptr           _M_parent;
  94     _Base_ptr           _M_left;
  95     _Base_ptr           _M_right;
  96 
  97     static _Base_ptr
  98     _S_minimum(_Base_ptr __x)
  99     {
 100       while (__x->_M_left != 0) __x = __x->_M_left;
 101       return __x;
 102     }
 103 
 104     static _Const_Base_ptr
 105     _S_minimum(_Const_Base_ptr __x)
 106     {
 107       while (__x->_M_left != 0) __x = __x->_M_left;
 108       return __x;
 109     }
 110 
 111     static _Base_ptr
 112     _S_maximum(_Base_ptr __x)
 113     {
 114       while (__x->_M_right != 0) __x = __x->_M_right;
 115       return __x;
 116     }
 117 
 118     static _Const_Base_ptr
 119     _S_maximum(_Const_Base_ptr __x)
 120     {
 121       while (__x->_M_right != 0) __x = __x->_M_right;
 122       return __x;
 123     }
 124   };

II.结点的插入
结点的插入主要分以下两个步骤：
1.我们首先以二叉查找树的方法增加节点并标记它为红色。（如果设为黑色，就会导致根到叶子的路径上有一条路上，多一个额外的黑节点，这个是很难调整的。但是设为红色节点后，可能会导致出现两个连续红色节点的冲突，那么可以通过颜色调换（color flips）和树旋转来调整。）
2.出现连红时做插入平衡操作

i.插入平衡操作（消除连红）
__x:需要做插入平衡操作的结点
__p:__x的父节点
__xpp：__x的祖父节点
__y：__x的叔父节点

出现连红(__x,__p为红色，__xpp为黑色)时会有以下三种情况（只看__p是__xpp左儿子的情况）
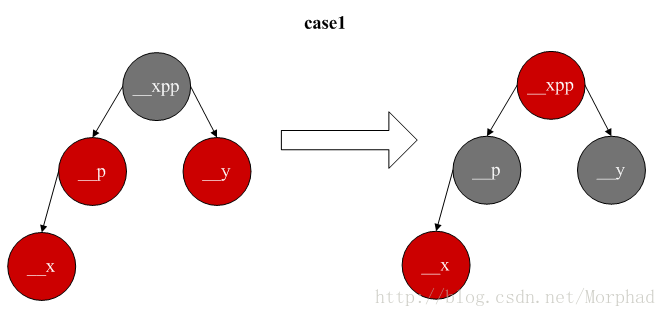
1.叔父节点是红色，则不能通过翻转/颜色调换使树重新平衡，只能做颜色调换并向祖父节点递归做平衡操作

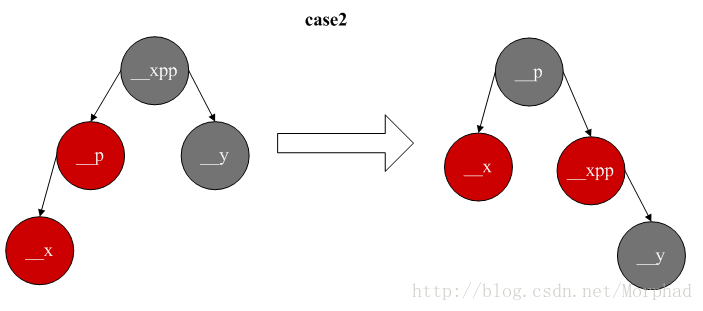
2.叔父节点是黑色，__x是__p的左儿子，通过祖父节点右翻转和颜色调换可使树平衡

3.叔父节点是黑色，__x是__p的右儿子，可以通过__p左翻转和颜色调换变成第二种情况，做相应的操作进而使树平衡

ii.结点插入实现

/* gcc-4.4.5/libstdc++-v3/src/tree.cc */
160   void
161   _Rb_tree_insert_and_rebalance(const bool          __insert_left,
162                                 _Rb_tree_node_base* __x,
163                                 _Rb_tree_node_base* __p,
164                                 _Rb_tree_node_bas