博弈论(游戏)

Bash Game 巴什博奕

n 个物品, 每次取走 1~m 个, 不能再取者输

结论: 当 n%(m+1)==0 时, 先手必败, 否则先手必胜

1 定义: 平等组合游戏

两人游戏, 轮流走步

有一个通常状态下有限的状态集, 有终止状态, 可以在有限步数内结束

规定了合法的状态转移, 且所有规定对双方一样生效

2 定义: N-position / P-position (先手必胜 / 必败状态)

则有三种转换

        无法进行任何移动的状态 (terminal position) 是 P-position

        可以移动到 P-position 的状态是 N-position

        任何移动都导致 N-position 的状态是 P-position

        (可以将当前状态需要操作的叫做先手)

Nim Game 尼姆博弈

n 堆物品, 第 i 堆有 ai 个, 每次取某堆中若干个(不能为0), 不能再取者输

结论: 当且仅当所有堆物品数异或起来结果为0时, 先手必败

尼姆博弈是 ICG (Impartial Combinatorial Games) 的一种

1 定义: ICG

两人游戏, 轮流走步

有一个通常状态下有限的状态集, 有终止状态, 可以在有限步数内结束

规定了合法的状态转移, 且所有规定对双方一样生效

对于任何一种可能的状态, 合法的移动集合只取决于这个状态本身, 不取决于何人操作、以前的任何操作、骰子的点数或其他因素

在尼姆博弈中, 可以通过 N-position / P-position 的三种转换求证结论, 如下

首先, 对于所有堆全为0的状态, 无法进行任何移动, 属于 P-position

其次, 对于 a1^a2^...^an == k (k!=0) 的状态, 必然存在一个 ai 变成 ai' 后满足 a1^a2^...^ai'^...^an == 0 , 即可以移动到 P-position 的状态, 属于 N-position

        (因为异或运算的性质, k 的二进制最高位必然来自于某个 ai , 则 ai^k 必然小于 ai , 令 ai' = ai^k , 则a1^a2^...^ai'^...^an == a1^a2^...^an^k == k^k == 0)

最后, 对于 a1^a2^...^an == 0 的状态, 必然不存在任何一个 ai 变成 ai' 后满足 a1^a2^...^ai'^...^an != 0 , 即任何移动都导致 N-position 的状态, 属于 P-position

        (假设存在一个 ai 满足上述条件, 则 a1^a2^...^ai^...^an == 0 且 a1^a2^...^ai'^...^an == 0 , 则 ai == ai' , 与题意矛盾, 故不存在)

综上所述, 任何 != 0 的状态均可转化成 == 0 的状态, 任何 == 0 的状态均不可转化成 != 0 的状态, 所以任何 == 0 的状态的最终结果一定是所有堆全为0的同样 == 0 的状态, 即先手必败, 证毕

接下来是 SG 函数

 1 定义: SG (Sprague Grundy) 函数

设当前状态为 S , SG(S) == mex{ SG(S') | S->S' }

其中 S->S' 表示状态 S 能到达状态 S' , mex 是 minimum excludant 的简称，即第一个未出现的最小非负整数, mex 运算是一个施加于集合的运算, 即 S 状态的 SG 值为最小的不属于这个集合的非负整数("这个集合"即 S 状态所能到达的所有 S' 状态的 SG 值集合), 如mex{0, 1, 2, 4} == 3

SG 函数可以在一个有向无环图中表示

对于图中任意一点 x , SG(x) == mex{ SG(y) | y 是 x 的后继}

可以推知 N-position 状态的SG值必然 >0 , P-position 状态的SG值必然 ==0; 

在巴什博奕中, SG(S.n) == n%(m+1) , S.n 表示剩余 n 个物品的情况, 这意味着每两次操作必然能从 n 个物品中取走 m+1 个(对于后手者最优), 余数为0时先手(此刻的操作者)必败, 余数非0时先手最终取走所有余数必胜

在尼姆博弈中, 对于每堆物品, SG(S.n) == n , S.n表示剩余 n 个物品的情况, 因为每次可以取走 >= 1 个, 故 SG(S.n) == mex{0, 1, 2, ... , n-1} == n, 即结论实际上是对每堆物品的 SG 值求总异或

当改变尼姆博弈中每次取 >= 1 个物品的规则时, 也可以通过计算每堆物品的 SG 值求总异或的方式得到结论

一堆物品用有向图的视角看, 每次操作相当于移动当前棋子前往子节点, 节点值 n 表示剩余 n 个物品的情况

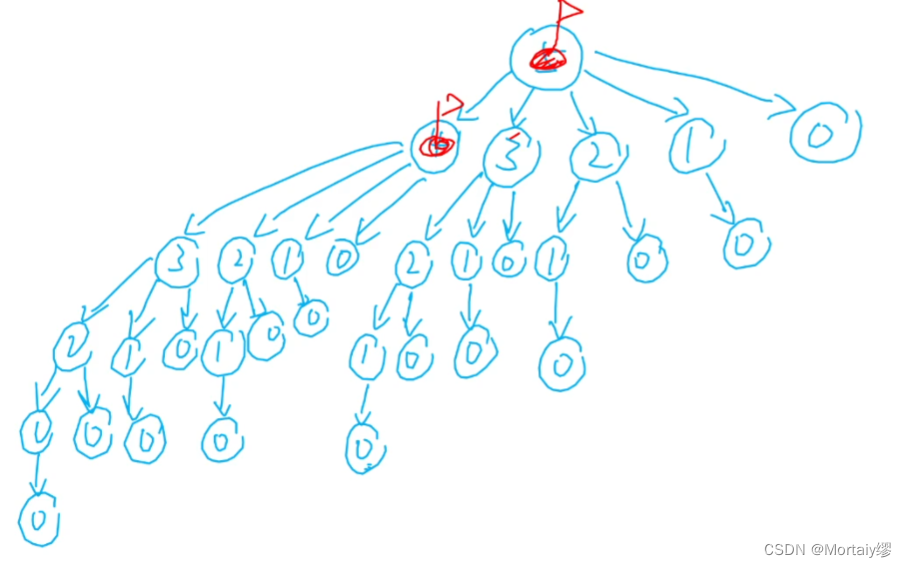
至此已经得出 SG 定理

2 定义: SG 定理

设 G1, G2, ... , Gn 是 n 个有向图游戏, 游戏 G 是这 n 个有向图游戏的和, G 的规则是任选一个 Gi 并移动上面的棋子, 则 SG(G) == SG(G1)^SG(G2)^...^SG(Gn) , 即游戏的和的 SG 值是它所有子游戏的 SG 值的异或和

任何一个 ICG 游戏都可以抽象成一个有向图游戏

例如:

        n堆石子, 每堆 ai 个, 每次可以从第一堆取1/2/3个, 可以从第二堆取奇数个, 可以从第三堆及以后的堆中取任意不为0个

        第一堆 SG 值为 ai%4

        第二堆 SG 值为 ai%2

        余下堆 SG 值为 ai

        最后将所有堆的 SG 值异或在一起得出结果