算法的时间复杂度大汇总(包括递归)
算法的时间复杂度大汇总
算法的时间复杂度也就是算法的时间度量,记作:
T
(
n
)
=
O
(
f
(
n
)
)
T(n) = O(f(n))
T(n)=O(f(n))
f(n)是问题规模为n的算法基本操作的次数。T(n)表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称「时间复杂度」。
T(n)和f(n)是同一数量级,但是T(n)只保留了“最高次项”且系数为1。
eg.
T
(
n
)
=
O
(
2
n
2
+
3
n
)
=
O
(
n
2
)
T(n) =O(2n^2+3n)=O(n^2)
T(n)=O(2n2+3n)=O(n2)
不同的时间复杂度类型
常数阶 O ( 1 ) O(1) O(1)
没有循环 执行次数和n无关
int i = 1;
int j = 2;
int k = i + j;
线性阶 O ( n ) O(n) O(n)
一层循环 循环里面的代码会执行n遍
int sum = 0;
for (int i = 0; i < n; i++) {
sum += i;
}
for (int i = 0; i < n; i++) {
// 时间复杂度为O(1)的语句块
}
平方阶 O ( n 2 ) O(n^2) O(n2)
两层循环 最内层循环里面的代码会执行n * n遍
for (int i = 0; i < n; i++) {
for(int j=0; j < n; j++) {
// 时间复杂度为O(1)的语句块
}
}
特殊的情况
for (int i = 0; i < n; i++) {
for(int j=i; j < n; j++) { // 注意j = i
// 时间复杂度为O(1)的语句块
}
}
f
(
n
)
=
n
+
n
−
1
+
.
.
.
+
1
=
n
2
2
+
n
2
⇒
O
(
n
2
)
f(n)=n+n-1+...+1=\frac{n^2}{2}+\frac{n}{2} \Rightarrow O(n^2)
f(n)=n+n−1+...+1=2n2+2n⇒O(n2)
对数阶 O ( l o g n ) O(logn) O(logn)
循环执行次数x满足
2
x
=
n
⇒
x
=
l
o
g
n
2^x=n \Rightarrow x=logn
2x=n⇒x=logn
tip: 循环变量是以2^i递增 再和问题规模n比较
int i = 1;
while(i<n)
{
i = i * 2;
}
线性对数阶 O ( n l o g n ) O(nlogn) O(nlogn)
时间复杂度为对数阶 O ( l o g n ) O(logn) O(logn)的代码循环n遍
for(int j = 0; j < n; j++){
int i = 1;
while(i<n)
{
i = i * 2;
}
}
指数阶 O ( 2 n ) O(2^n) O(2n)
递归的时间复杂度计算在后文会进行讲解
int Fibonacci(int n)
{
if (n <= 1) return n;
return Fibonacci(n - 2) + Fibonacci(n - 1);
}
特殊要点
带分支结构
总的时间复杂度等于时间复杂度最大的路径的时间复杂度
// 时间复杂度为O(n^2)
if (n >= 0) {
// 第一条路径时间复杂度为 O(n^2)
} else {
// 第二条路径时间复杂度为 O(n)
}
多个循环
假设循环体的时间复杂度为 O(n),循环次数为 m,则这个循环的时间复杂度为 O(m×n)
for (int i = 0; i < m; i++) {
for(int j=i; j < n; j++) { // 注意j = i
// 时间复杂度为O(1)的语句块
}
}
时间复杂度排序
O
(
1
)
<
O
(
l
o
g
n
)
<
O
(
n
)
<
O
(
n
l
o
g
n
)
<
O
(
n
2
)
<
O
(
n
3
)
<
O
(
2
n
)
<
O
(
n
!
)
<
O
(
n
n
)
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
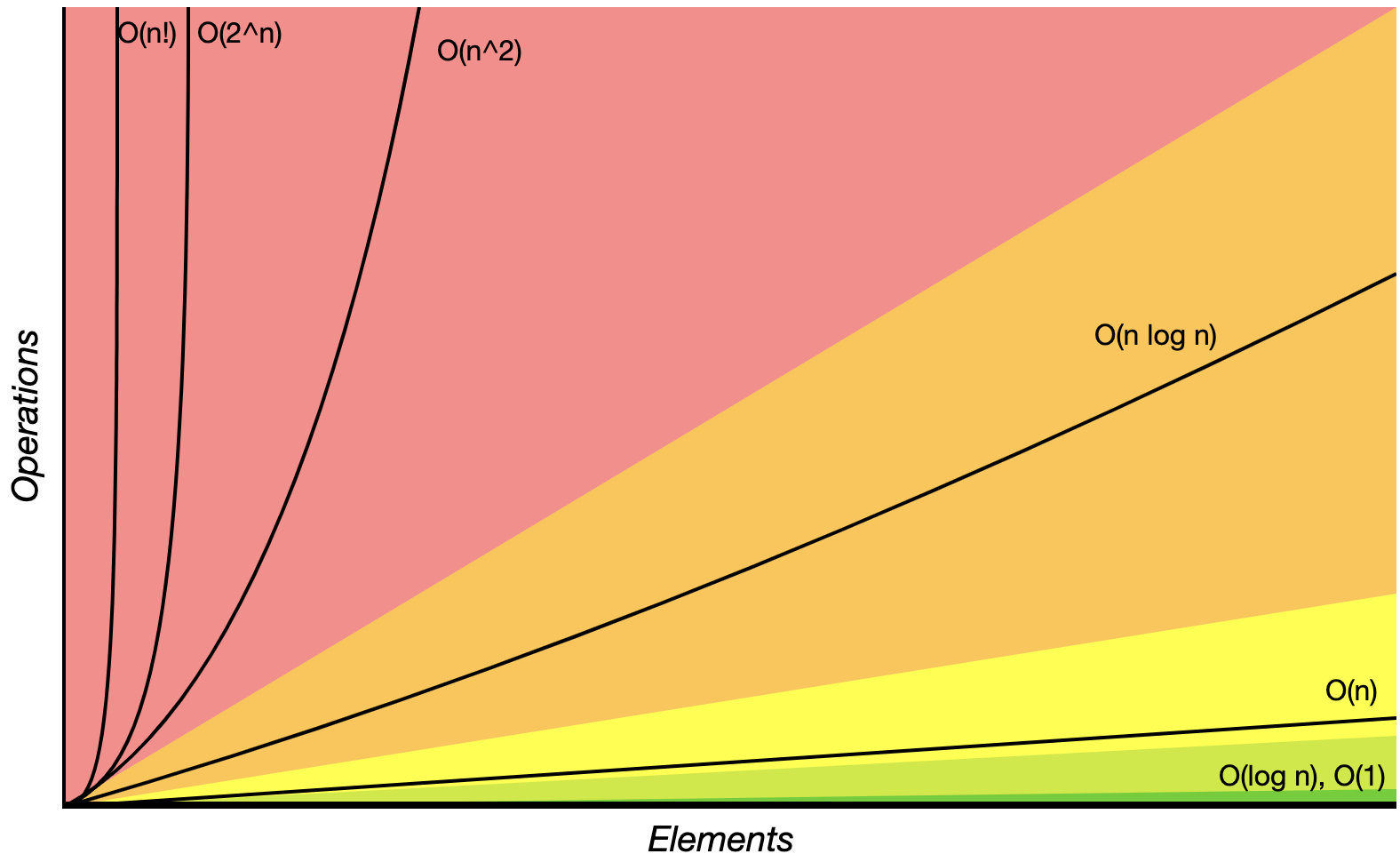
平均时间复杂度
如果算法中基本操作重复执行次数会根据问题的输入数据集不同而不同,会使用平均时间复杂度
多用于排序算法,一般会假设出现n!种排列情况的概率相等
eg.快速排序 平均
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn) 最差
O
(
n
2
)
O(n^2)
O(n2)
递归的时间复杂度计算
对递归的时间复杂度计算有很多有效方法,这里重点介绍递归树(Recursive Tree)和主定理法(Master Method)。
递归的时间复杂度计算的三个要点
- 递归函数体的时间复杂度f(n)
- 递归函数的调用层数
- 递归函数的分支数(也就是函数体内调用了自己几次)
方法1:递归树
递归树是一棵结点带权值的树。初始的递归树只有一个结点,它的权标记为T(n);然后按照递归树的迭代规则不断进行迭代,每迭代一次递归树就增加一层,直到树中不再含有权值为函数的结点(即叶结点都为T(1))
- 递归树的结点:递归函数体的时间复杂度f(n)
- 递归树的结点的度(分支数):递归函数分支数
- 递归树的深度:递归函数的层数
例子1 汉诺塔
// 这个函数大概知道是那么个意思就行
void Hanoi(int num, vector<int>& x, vector<int>& y, vector<int>& z)
{
if(num == 1)
{
move(x, z);
return;
}
Hanoi(num - 1, x, z, y); // x -> y
move(x, z);
Hanoi(num - 1, y, x, z); // y -> z
}
递归方程
T
(
n
)
=
2
T
(
n
−
1
)
+
O
(
1
)
T(n)=2T(n-1)+O(1)
T(n)=2T(n−1)+O(1)
由递归方程作递归树(最右侧是该层执行总次数)如下
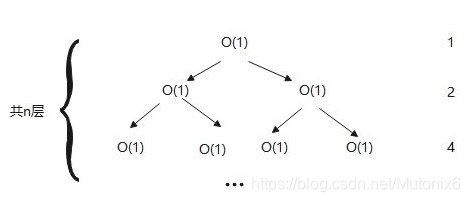
f
(
n
)
=
1
+
2
+
4
+
.
.
.
+
2
n
−
1
=
2
n
−
1
⇒
O
(
2
n
)
f(n) = 1+2+4+...+2^{n-1}=2^n-1 \Rightarrow O(2^n)
f(n)=1+2+4+...+2n−1=2n−1⇒O(2n)
例子2 斐波那契数列
int Fibonacci(int n)
{
if (n <= 1) return n;
return Fibonacci(n - 2) + Fibonacci(n - 1);
}
递归方程 T ( n ) = T ( n − 1 ) + T ( n − 2 ) + O ( 1 ) T(n)=T(n-1)+T(n-2)+O(1) T(n)=T(n−1)+T(n−2)+O(1)
(不严谨的分析)
这个类似于汉诺塔 但不太一样
递归树的前绝大部分层的结点的度均为2,最后几层左边多 右边少(非满二叉树)
- 如果一直n-1 则有n层
- 如果一直n-2 则不到n层
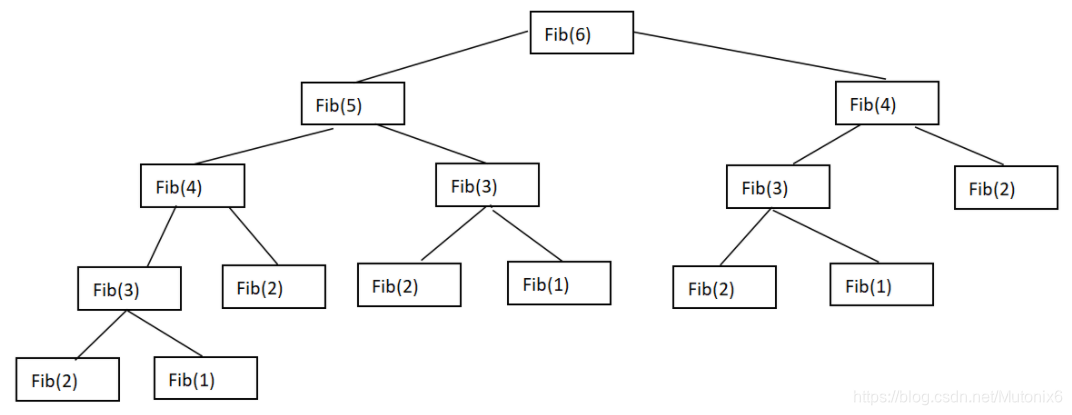
所以该算法的执行次数接近2^n 所以时间复杂度为
O
(
2
n
)
O(2^n)
O(2n)
例子3 典型类型
递归方程 T ( n ) = a T ( n b ) + O ( f ( n ) ) T(n)=aT(\frac{n}{b})+O(f(n)) T(n)=aT(bn)+O(f(n))
- 递归树的结点 : O ( f ( n ) ) O(f(n)) O(f(n))
- 递归树的结点的度(分支数): a a a
- 递归树的深度 : l o g b n log_{b}n logbn
具体例子
T
(
n
)
=
2
T
(
n
2
)
+
n
2
T(n)=2T(\frac{n}{2})+n^2
T(n)=2T(2n)+n2
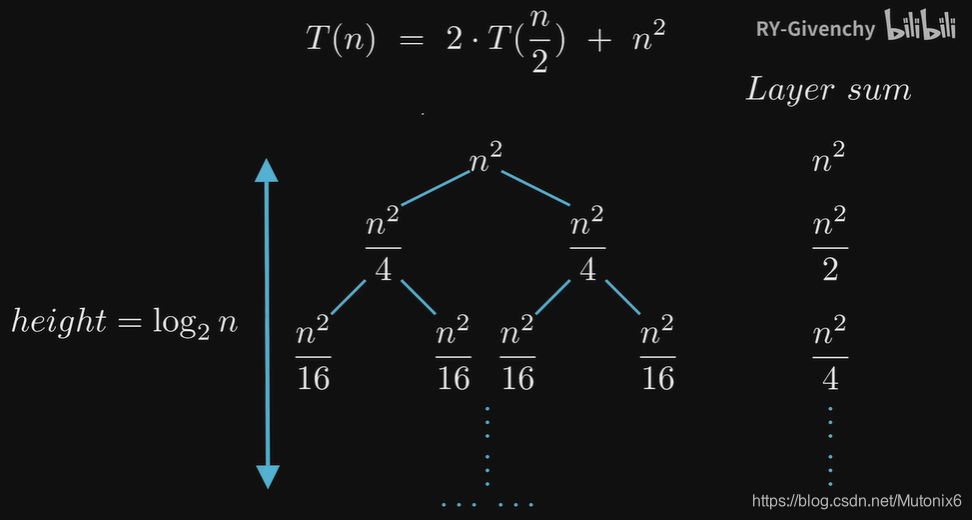
- 递归树的每一层相当于一个等比数列
总的时间复杂度为等比数列求和
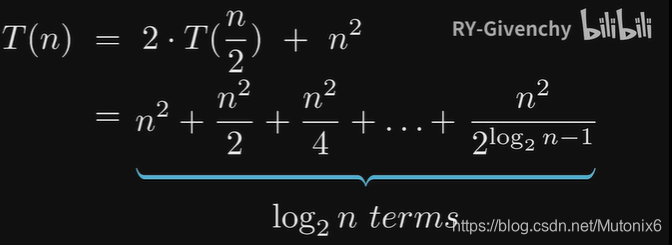

该递归方程的时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)
方法2:主定理
主定理适合解决类似上述例子3中典型类型的时间复杂度
注意 f(n) = n^d
T
(
n
)
=
a
T
(
n
b
)
+
O
(
n
d
)
T(n)=aT(\frac{n}{b})+O(n^d)
T(n)=aT(bn)+O(nd)
- 递归树的结点 : O ( n d ) O(n^d) O(nd)
- 递归树的结点的度(分支数): a a a
- 递归树的深度 : l o g b n log_{b}n logbn
公式形式
T ( n ) = { O ( n l o g b a ) l o g b a > d O ( n l o g b a l o g b n ) l o g b a = d O ( n d ) l o g b a < d T(n)=\left\{ \begin{aligned} &O(n^{log_{b}a}) & log_{b}a >d\\ &O(n^{log_{b}a}log_{b}n) &log_{b}a=d\\ &O(n^d) &log_{b}a<d \end{aligned} \right. T(n)=⎩⎪⎪⎨⎪⎪⎧O(nlogba)O(nlogbalogbn)O(nd)logba>dlogba=dlogba<d
直观解释
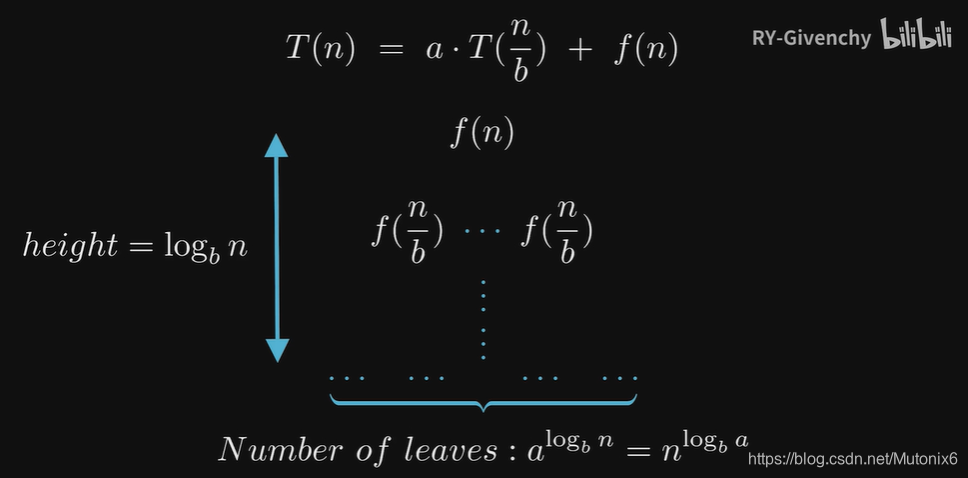

情况1: n l o g b a > n d n^{log_{b}a} >n^d nlogba>nd
叶子结点分裂的速度大于递归函数体本身(根结点)
大部分计算量集中递归树的最后一层
时间复杂度由叶子结点主导
情况2: n l o g b a = n d n^{log_{b}a} =n^d nlogba=nd
叶子结点分裂的速度等于递归函数体本身(根结点)
时间复杂度由二者共同主导
示例 归并排序
vector<int>& Msort(vector<int> &vec)
{
if(vec.size() == 1)
return vec;
int m = vec.size() / 2;
// vector 切片操作
vector<int> vec1(vec.begin(), vec.begin() + m);
vector<int> vec2(vec.begin() + m, vec.end());
// 均分为两块进行排序
vec1 = Msort(vec1);
vec2 = Msort(vec2);
vec = merge(vec1, vec2); // merge是另外自己写的函数
return vec;
}
归并排序的递归方程
T
(
n
)
=
2
T
(
n
2
)
+
O
(
n
)
T(n) = 2T(\frac{n}{2})+O(n)
T(n)=2T(2n)+O(n)
由主定理 得到时间复杂度为
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)

可以总结的规律是 情况2中 递归树每一层的总计算量都等于递归函数体(根结点)的
O
(
n
d
)
O(n^d)
O(nd),共有
l
o
g
b
n
层
log_{b}n层
logbn层
情况3: n l o g b a < n d n^{log_{b}a} <n^d nlogba<nd
递归函数体本身(根结点)大于叶子结点分裂的速度
大部分计算量集中递归树的根结点
时间复杂度由根结点主导
参考
这篇文章作为我个人学习的记录 十分感谢以下提供的帮助
十分钟搞定时间复杂度
时间复杂度到底怎么算
斐波那契数列递归算法的时间复杂度计算
如何计算时间复杂度 b站up RY-Givenchy
主定理直观理解




















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








