【算法修炼】图论算法一（图的表示、图的遍历、图中环的检测）

@u@

已于 2022-08-07 21:59:18 修改

阅读量1.3k

点赞数 3

分类专栏：算法修炼文章标签：算法图论数据结构

于 2022-02-21 17:04:59 首次发布

本文链接：https://blog.csdn.net/Mxeron/article/details/123046028

版权

算法修炼专栏收录该内容

47 篇文章 19 订阅

订阅专栏

学习自：https://labuladong.gitee.io/algo/2/19/35/

终于开始了数据结构算法的学习…（😰数据结构）

图论算法一

一、图的基本结构

![在这里插入图片描述](https://img-blog.csdnimg.cn/1a51429919214df0ab13fc67f29418bf.png

二、图的存储方式

图结构的两种存储方式：
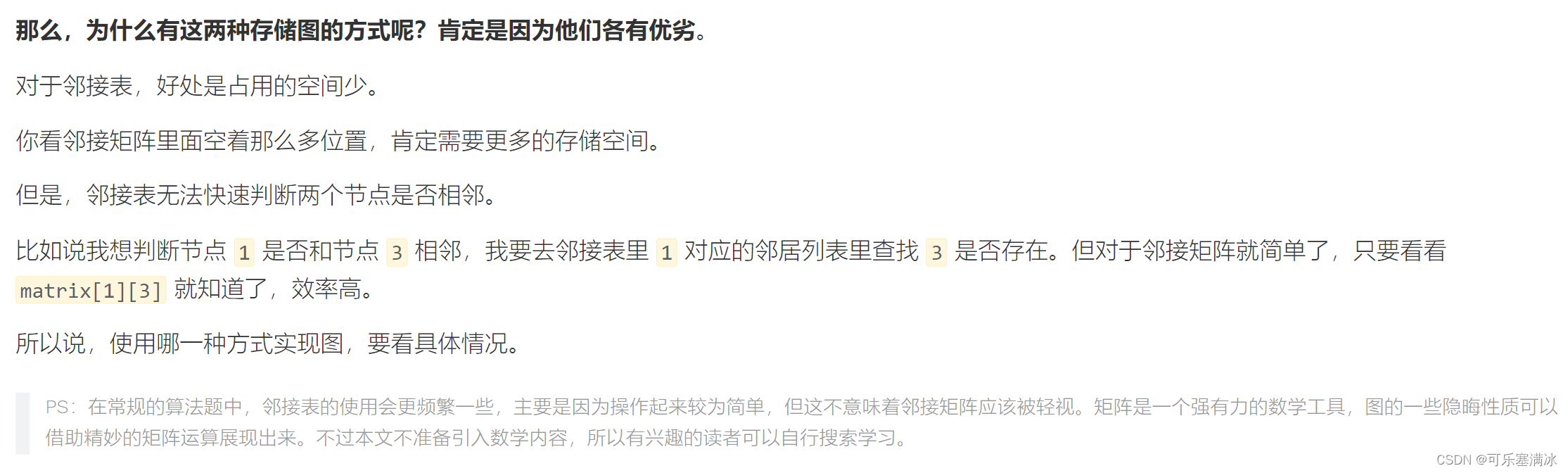
在这里插入图片描述

无向图的邻接矩阵一定是对称的。

三、度

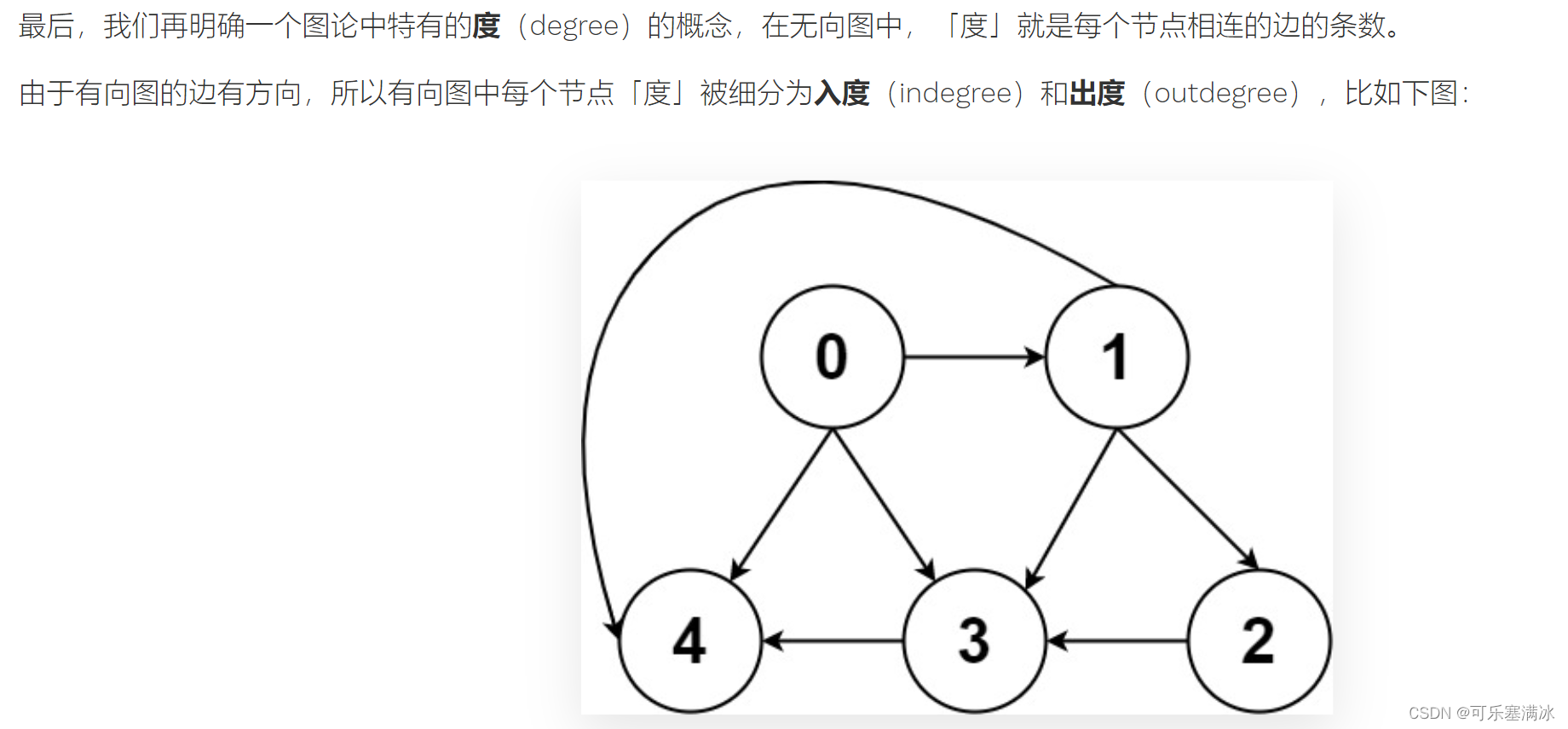
在这里插入图片描述

四、图的遍历

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。

所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：

// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

上面的图遍历方式属于DFS，深度优先搜索。一定要把这里图的遍历与回溯算法区分开，不可混为一谈。

使用visited数组是为了避免有环图中的循环访问。
在这里插入图片描述
上述 GIF 描述了递归遍历二叉树的过程，在 visited 中被标记为 true 的节点用灰色表示，在 onPath 中被标记为 true 的节点用绿色表示。

onPath的撤销操作，类似于回溯算法中的回溯，但是撤销的位置有所不同。onPath在for循环外面，回溯是在for循环里面。

所有可能的路径（中等）

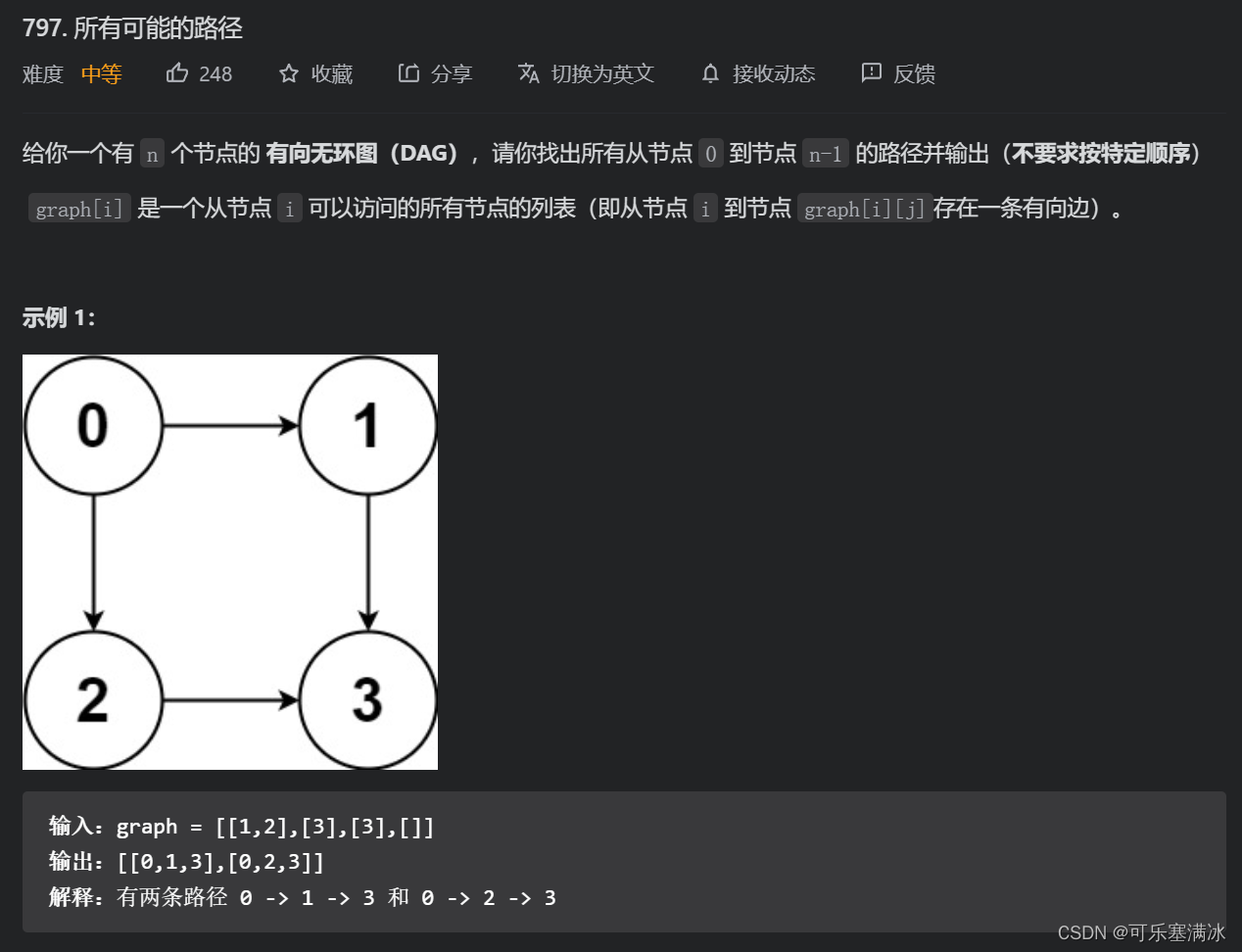
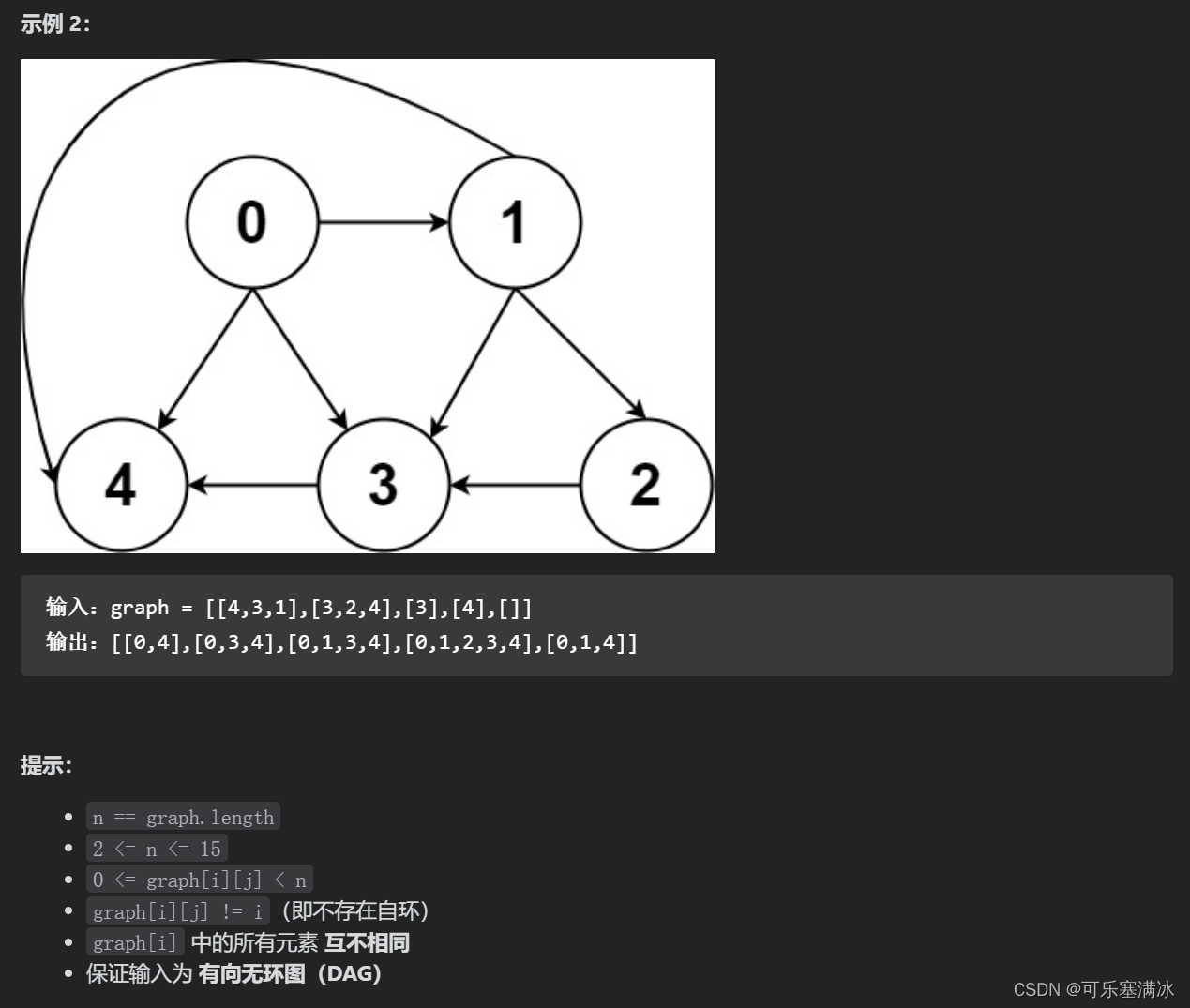
在这里插入图片描述

本题主要是考察对图的遍历，图结构是按照邻接表存储的，本题不存在环，所以不需要使用visited数组。

class Solution {
    List<List<Integer>> ans = new LinkedList<>();
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        int n = graph.length;
        LinkedList<Integer> tmp = new LinkedList<>();
        tmp.add(0);
        traverse(graph, 0, n, tmp);
        return ans;
    }
    void traverse(int[][] graph, int s, int n, LinkedList<Integer> tmp) {
        if (s == n - 1) {
            // 说明到达了节点n-1
            ans.add(new LinkedList(tmp));
            return;
        }
        // 遍历该节点的下一个节点
        for (int next : graph[s]) {
            tmp.add(next);
            traverse(graph, next, n, tmp);
            tmp.removeLast();
        }
    }
}

一定要注意，递归遍历是遍历当前结点的相邻结点，移除结点是在for循环外部移除。

五、图的环检测

有向图的环检测

课程表（中等）

在这里插入图片描述
prerequisites = [[1,0]]，指的是学习1课程之前必须先学习课程0。 就相当于是一个图中，0指向1，代表必须修了0才能修1。

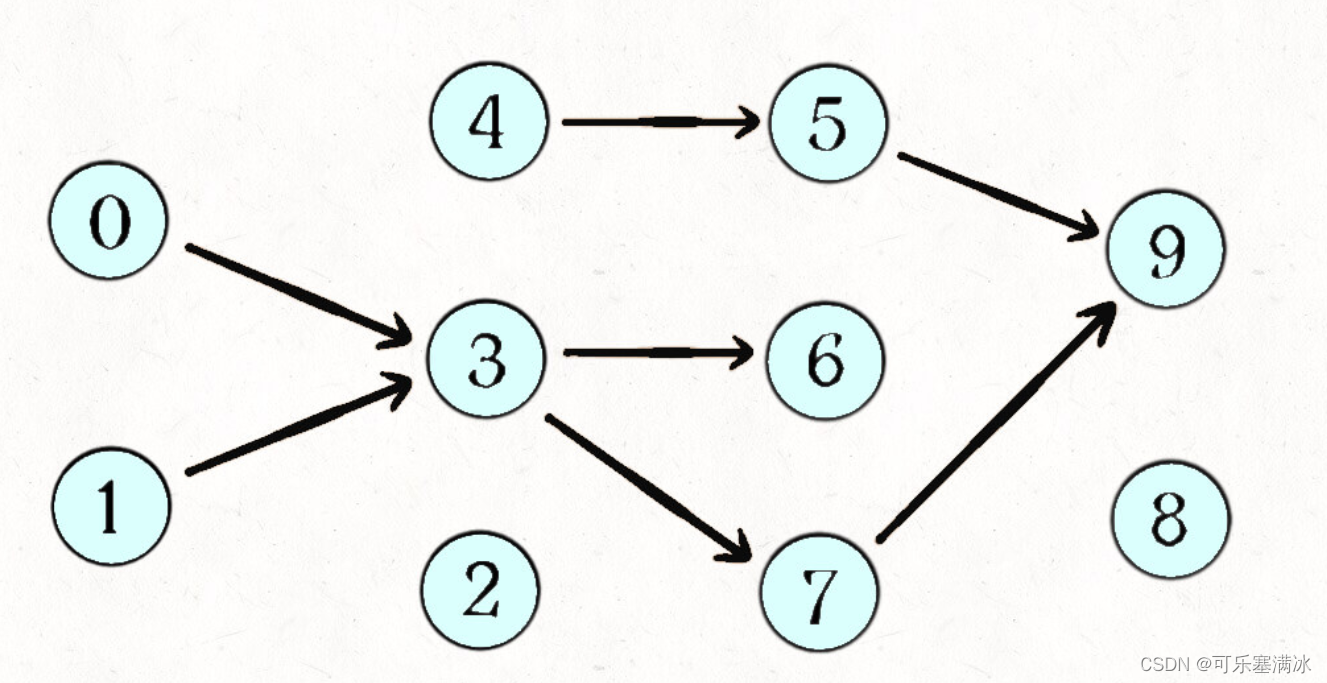
那么，是否能完成所有课程的学习，取决于这个图是否存在环？ 如果有环，那肯定就不能全部修完，存在重复依赖了。所以问题，就转换为检测图中的环。

首先需要存储图结构，图结构最好选用邻接表进行存储，可以使用下面的结构存储：

List<Integer>[] graph;

graph是一个列表，里面存储着图中的一个个结点，graph[0]代表0结点相连的结点情况。

建图函数可以仿照下面的方式书写：用List更加方便存储和删除，数组一直需要记录下标

List<Integer>[] builddGraph(int numCourses, int[][] prerequisites) {
    // 图中有 numCourses 个结点
    List<Integer>[] graph = new LinkedList[numCourses];
    for (int i = 0; i < numCourses; i++) {
        graph[i] = new LinkedList<>();
    }
    for (int[] edge : prerequisites) {
        // [0,1]，0 <- 1，修 0之前必须先修 1
        int from = edge[1], to = edge[0];
        // 添加一条边从 from 指向 to
        graph[from].add(to);
    }
    return graph;
}

图建好了，下面就是遍历。

// 防止遍历同一个节点
boolean[] visited;
// 从节点 s 开始 DFS 遍历，将遍历过的节点标记为true
void traverse(List<Integer>[] graph, int s) {
    if (visited[s]) {
        return;
    }
    /* 前序遍历代码位置 */
    // 将当前节点标记为已遍历
    visited[s] = true;
    // DFS遍历与当前结点相连的结点
    for (int t : graph[s]) {
        traverse(graph, t);
    }
    /* 后续遍历代码位置 */
}

上面只是一个结点的遍历过程，由于本题中并不是所有结点都相连，所以必须得对每个结点都进行遍历。

// 防止重复遍历同一个节点
boolean[] visited;

boolean canFinish(int numCourses, int[][] prerequisites) {
    List<Integer>[] graph = buildGraph(numCourses, prerequisites);
    
    visited = new boolean[numCourses];
    for (int i = 0; i < numCourses; i++) {
    	// 对每个结点都要进行dfs遍历
        traverse(graph, i);
    }
}

void traverse(List<Integer>[] graph, int s) {
    // 代码见上文
}

现在可以思考如何判断这幅图中是否存在环。可以把 traverse 看做在图中节点上游走的指针，只需要再添加一个布尔数组 onPath 记录当前 traverse 经过的路径。

// 当前traverse经过的路径（为true的结点）
// 如果当前traverse遍历到的结点已经在onPath中出现过了，那就是成环了(onPath = true)
boolean[] onPath;
// 避免重复访问
boolean[] visited;
boolean hasCycle = false;

// DFS遍历
void traveeerse(List<Integer>[] graph, int s) {
    if (onPath[s]) {
        // 发现环
        hasCycle = true;
    }
    // 有环，或者当前结点被访问，那就return
    if (visited[s] || hasCycle) {
        return;
    }
    // 结点s标记为已遍历
    visited[s] = true;
    // 当前结点加入路径中
    onPath[s] = true;
    // 开始遍历结点 s 相连的结点
    for (int t : graph[s]) {
        traveeerse(graph, t);
    }
    // 结点 s 遍历完成，回溯到上一个结点
    onPath[s] = false;
}

类比贪吃蛇游戏，visited 记录蛇经过过的格子，而 onPath 仅仅记录蛇身。onPath 用于判断是否成环，类比当贪吃蛇自己咬到自己（成环）的场景。

综上，可以写出完整本题代码：

class Solution {
    // 记录每个节点是否访问过
    boolean[] vis;
    // 记录当前访问路径上的节点
    boolean[] onPath;
    boolean hasCycle = false;
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 如果要学习课程 ai 则 必须 先学习课程  bi
        // 根据课程关系建图
        List<Integer>[] graph = new LinkedList[numCourses];
        int n = prerequisites.length;
        for (int i = 0; i < numCourses; i++) graph[i] = new LinkedList<>();
        for (int[] cur : prerequisites) {
            // cur[1] -> cur[0]
            // 有向图
            graph[cur[0]].add(cur[1]);
        }
        vis = new boolean[numCourses];
        onPath = new boolean[numCourses];
        // 有环则说明不能完成
        for (int i = 0; i < numCourses; i++) {
            vis[i] = true;
            onPath[i] = true;
            dfs(graph, i);
            onPath[i] = false;
        }
        return !hasCycle;
    }
    void dfs(List<Integer>[] graph, int cur) {
        if (hasCycle) return;  // 已经有环就不用再找了
        for (int next : graph[cur]) {
            // 一定要先判断onPath
            // 如果要先判断vis,如果是onPath,一定也是vis,所以无法判断环
            if (onPath[next]) {
                hasCycle = true;
                return;
            }
            if (vis[next]) continue;
            // 记录全局节点访问情况
            vis[next] = true;
            // 记录当前路径的节点访问情况
            onPath[next] = true;
            dfs(graph, next);
            // 回溯(只需要回溯当前路径上节点的访问情况)
            onPath[next] = false;
        }
    }
}

更推荐的是使用BFS + 入度统计的方式判断环，因为这可以直接用于拓扑排序，此时队列中的出队顺序就是拓扑排序的结果：

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 建图
        List<Integer>[] graph = new LinkedList[numCourses];
        for (int i = 0; i < numCourses; i++) graph[i] = new LinkedList<>();
        // 统计每个节点的入度信息
        int[] indegree = new int[numCourses];
        for (int[] cur : prerequisites) {
            // 学习a之前必须先学习b
            graph[cur[1]].add(cur[0]);
            indegree[cur[0]]++;
        }
        Queue<Integer> queue = new LinkedList<>();
        // 先把入度=0的节点入队，它们是开始节点
        for (int i = 0; i < numCourses; i++) {
            if (indegree[i] == 0) {
                queue.offer(i);
            }
        }
        // 统计访问过的点
        int visited = 0;
        while (!queue.isEmpty()) {
            int cur = queue.poll();
            // 访问过的点++
            visited++;
            // 遍历与其相连的点
            for (int next : graph[cur]) {
                // 相连的点的入度--
                indegree[next]--;
                // 入度=0再入队
                if (indegree[next] == 0) {
                    queue.offer(next);
                }
            }
        }
        return visited == numCourses;
    }
}

本质是模拟逐个课程节点被删除的过程。

无向图的环检测

用上面的方法依然可以，一般无向图在建图时需要记录两条边，因为从1到2的同时，存在从2到1。在进行无向图的环检测时，只进行一条边的统计，比如1到2，只记录从1到2，而不记录从2到1，这样就可以实现环检测。

六、拓扑排序

课程表Ⅱ（中等）

在这里插入图片描述
这一题是上一题的升级版，上一题只需要判断环，本题不仅要判断环，还要使用拓扑排序，确定出能够修完所有课的顺序。

在这里插入图片描述
有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

先看看如何生成拓扑排序：
1、从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
2、从图中删除该顶点和所有以它为起点的有向边。
3、重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
在这里插入图片描述
于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。通常，一个有向无环图可以有一个或多个拓扑排序序列。

其实也不难看出来，如果把课程抽象成节点，课程之间的依赖关系抽象成有向边，那么这幅图的拓扑排序结果就是上课顺序。

其实特别简单，将后序遍历的结果进行反转，就是拓扑排序的结果。

后续内容见：图论算法二

@u@

关注

3
点赞
踩
5

收藏

觉得还不错? 一键收藏
打赏
0
评论
【算法修炼】图论算法一（图的表示、图的遍历、图中环的检测）

学习自：https://labuladong.gitee.io/algo/2/19/35/终于开始了数据结构算法的学习…（????数据结构）一、图的基本结构二、图的存储方式图结构的两种存储方式：无向图的邻接矩阵一定是对称的。三、度四、图的遍历图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：// 记录被遍历过的节点boolean[] visited;//
复制链接

扫一扫