前面已经学习了二叉树的创建,以及一些class的基本功能 。
本文实现了对二叉树的递归遍历和非递归遍历,当然还包括了一些栈操作。
二叉树的遍历本质上就是出栈和入栈的过程 。遍历的递归方式简单又容易理解,但是效率始终是个问题。
非递归算法可以清楚地知道遍历的每一个细节,但是就不容易理解。
遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历,中序遍历,后序遍历。
前序遍历:根节点->左子树->右子树
中序遍历:左子树->根节点->右子树
后序遍历:左子树->右子树->根节点
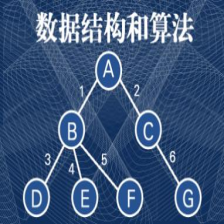
以下面的二叉树为例,先给出遍历的结果 ,然后对比程序结果:
前序遍历:0 134 256
中序遍历:314 0 526
后序遍历:341 526 0
首先给出二叉树节点:
struct BinaryTreeNode
{
typedef BinaryTreeNode* Treepoint ;
BinaryTreeNode(const T& data)
:_data(data)
, pLeft(NULL)
, pRight(NULL)
{}
char _data;
Treepoint pLeft;
Treepoint pRight;
};利用C++特有的类把整个数都封装起来吧 , 在加入遍历操作。
这里遍历操作知识输出节点中的数字。
首先,用先序创建一个二叉树
class BinaryTree
{
public:
BinaryTree()
:_pRoot(NULL)
{}
BinaryTree(char arr[], size_t sz)
{
size_t index = 0;
_CreatNode(_pRoot, arr, sz, index);
}
private:
BinaryTreeNode* _pRoot;
protected:
void _CreatNode(BinaryTreeNode*& Root, char arr[], size_t sz, size_t& index)
{ //传的是引用 //引用
if (index < sz && arr[index] != '?')
{
//前序遍历 :创建过程 根-左-右
Root = new BinaryTreeNode(arr[index]);
_CreatNode(Root->pLeft, arr, sz, ++index);
_CreatNode(Root->pRight, arr, sz, ++index);
}
}
};递归实现
<pre name="code" class="cpp"><span style="color:#ffffff;background-color: rgb(51, 204, 0);">//前序遍历 根- 左 - 右</span><span style="background-color: rgb(255, 255, 255);">
void _PreOrder(BinaryTreeNode* Root)const
{
if (Root != NULL)
{
cout << Root->_data << ' ';
if (Root->pLeft != NULL)
{
_PreOrder(Root->pLeft); //往左
}
if (Root->pRight != NULL)
{
_PreOrder(Root->pRight); //往右
}
}
}
</span><span style="background-color: rgb(51, 204, 0);">//中序遍历 左- 根 - 右</span><span style="background-color: rgb(255, 255, 255);">
void _InOder(BinaryTreeNode* Root)const
{
if (Root != NULL)
{
_InOder(Root->pLeft);
cout << Root->_data << ' ';
_InOder(Root->pRight);
}
}
</span><span style="background-color: rgb(51, 204, 0);">//后序遍历:左 - 右 - 根</span><span style="background-color: rgb(255, 255, 255);">
void _PostOrder(BinaryTreeNode* Root)const
{
if (Root != NULL)
{
_PostOrder(Root->pLeft);
_PostOrder(Root->pRight);
cout << Root->_data << ' ';
}
}</span>非递归实现
递归实现一看就懂,但是遍历的非递归实现还是有点麻烦的,下面就一一讲述。
前序遍历
还是对上面那棵树,它的前序遍历:0 134 256
分析:前序遍历的顺序是 根->左节点->右节点 。
在递归实现的时候其实就是使用一个栈,将节点中的数据压栈,当不满足递归条件的时候,就会依次出栈,从而实现了前序遍历。那么我们在使用 循环 来实现二叉树的前序遍历的时候,就需要自己创建一个栈,并且对元素入栈和出栈的顺序要把握好。(这也就是为什么我们在下面循环中使用栈的原因 ,很多博客都没提及,对于基础差的还是需要点出来的)
还得重复一句:所有的节点都可看做是根节点。根据思维走向,就能搞定前序遍历的代码了。
实现代码:
void PreOrder()
{
if (this->_pRoot != NULL)
{
stack<BinaryTreeNode<T>* > Order;
Order.push(_pRoot);
while (!Order.empty())
{
BinaryTreeNode<T> * pCur = Order.top();//每次记住栈顶位置,方便下面找 左右子树
cout << pCur->_data << ' ';
Order.pop();
if (pCur->pRight != NULL)
{
Order.push(pCur->pRight); //先把右字树 压栈
}
if (pCur->pLeft != NULL)
{
Order.push(pCur->pLeft);// 左子树 作为栈底
}
}
}
}在写上面的代码时,我有突发奇想,感觉感觉代码也可以这么写:
void PreOrder_2()
{
if (this->_pRoot)
{
stack<BinaryTreeNode*> Order;
BinaryTreeNode* pCur = _pRoot;
while (!Order.empty() || pCur)
{
//边遍历边打印,压栈 直到找到最左边的节点
while (pCur != NULL)
{
cout << pCur->_data << ' ';
Order.push(pCur);
pCur = pCur->pLeft;
}
//pCur== NULL 说明已经根和节点都已经遍历了,下面进入右子树
//依次释放,找到节点的右节点
if (!Order.empty())
{
pCur = Order.top();
pCur = pCur->pRight;
Order.pop();
}
}
}
}如果你看懂了,那么下面的解释你也没必须看了。
解释:首先,在写第一种前序遍历的代码时,每次访问完节点后,又把栈释放了,这样不停地入栈出栈很麻烦。所以就想出解决这个问题的办法: 从根节点到左子树的最左边节点 边访问边入栈,当访问完左子树的时候,在访问右子树的时候就可以 出栈同时找右子树的节点其实,我觉得上这个方法的代码还以以再改变一下(这样就变成了和第一种方法一样的效果了
 ):
):
void PreOrder_3()
{
if (this->_pRoot)
{
stack<BinaryTreeNode*> Order;
BinaryTreeNode* pCur = _pRoot;
while (!Order.empty() || pCur)
{
//边遍历边打印,压栈 直到找到最左边的节点
if (pCur != NULL)
{
cout << pCur->_data << ' ';
Order.push(pCur);
pCur = pCur->pLeft;
}
else
{
pCur = Order.top();
pCur = pCur->pRight;
Order.pop();
}
}
}
}好了 ,前序遍历就到这里了
中序遍历
中序遍历的顺序: 左孩子 - 根节点 - 右孩子
同样,中序遍历也需要使用栈,然后又是压栈访问出栈的过程了。其实,写到这里 感觉上面的想法和class的构造函数是一样的,当用类构造函数的时候,首先调用构造函数 然后再进行其他操作 , 最后析构掉 , 在二叉树遍历的过程 就是 首先压栈 然后在进行访问 最后出栈。(PS: 这也许是在写博客的过程中的自我思考吧)
一句话: 让代码跟着思维走
实现代码如下:
void MidOrder()
{
BinaryTreeNode<T>* pCur = _pRoot;
stack<BinaryTreeNode<T>* > Node;
while (pCur != NULL || !Node.empty())
{
while (pCur != NULL)
{
Node.push(pCur);
pCur = pCur->pLeft;
}
BinaryTreeNode<T>* pTop = Node.top();
if (pTop->pRight != NULL)
{
pCur = pTop->pRight;
}
cout << pTop->_data << ' ';
Node.pop();
}
}
从前序遍历可以想到中序遍历也可以这么写:
void MidOrder_1()
{
if (this->_pRoot)
{
BinaryTreeNode* pCur = _pRoot;
stack<BinaryTreeNode*> Order;
while (!Order.empty() || pCur)
{
if (pCur)
{
Order.push(pCur);
pCur = pCur->pLeft;
}
else
{
pCur = Order.top();
Order.pop();
cout << pCur->_data << ' ';//访问在这
pCur = pCur->pRight;
}
}
}
}
后序遍历
后序遍历的顺序:左- 右 - 根
个人觉得后序遍历是最难的了,在后序遍历中,要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点,这就为流程的控制带来了难题。我也是花了不少时间才搞懂的。
代码如下:
void PostOrder()
{
// 利用栈 保存寻找最左边节点的路径,检测右边是否有子节点,若无出栈(保存上一次的栈顶,以防死循环);若有则入栈
BinaryTreeNode<T>* pCur = _pRoot;
stack<BinaryTreeNode<T>* > Node;
BinaryTreeNode<T>* Prev = NULL;//保存上次栈顶的位置
while (pCur != NULL || !Node.empty())
{
while (pCur != NULL) //找到最左边的 , 并保存路径
{
Node.push(pCur);
pCur = pCur->pLeft;
}
BinaryTreeNode<T>* pTop = Node.top();
if (pTop->pRight == NULL || pTop->pRight == Prev)//防止不停地存pRight和出pRight
{
cout << pTop->_data << ' ';
Node.pop();
Prev = pTop;
}
else
{
pCur = pTop->pRight;
}
}
}解析:先找到二叉树最左边的节点,并且保存找这个节点的路径
然后判断最后一个节点的右子树是否为空,若为空则 访问 ->出栈 ;若不为空 则访问右子树
同时判断Prev(上一次循环的栈顶元素)当本次访问的节点的右子树为上次访问的节点时,也要出栈,不然就会造成死循环了 !!!
学习的一点总结吧:
其实,在学习数据结构的过程中,我们需要不断的思考并验证自己的思考,在想不出怎么解决问题方法的时候,要多看书上是怎么写的,当有一点想法的时候,我们要写出自己的思路,不断的完善自己的思路,同时看看网上那些大神是怎么解决问题的 , 然后顺着思路把代码敲出来,一步步调试,发现问题,解决问题 ,最后总会写出来的。
数据结构确实是个“磨人的小妖精”,对我来说确实挺难的, 这就需要 对这门课程很有耐心,调试代码也要细心,不懂的多思考 看书。
























 808
808











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








