位运算

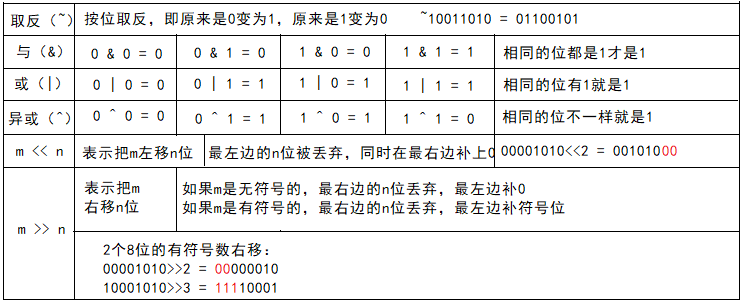
位运算是针对二进制的运算，也就是说进行位运算是需要先把数据转换成二进制。位运算总共有6种运算：按位取反（~）、与（&）、或（|）、异或（^）、左移（<<）、右移（>>）。运算规律如下图所示：

下面是有关位运算的题：

//二进制中1的个数
int GetNumber1(int n)//除法，没有办法处理负数
{
	int count = 0;
	while(n)
	{
		if(n%2 != 0)
		{
			count++;
		}
		n /= 2;
	}
	return count;
}

/*int GetNumber2(int n)//右移1位
{
	int count = 0;
	while(n)
	{
		if(n & 1)//如果n是负数，左边补1，陷入死循环
		{
			count++;
		}
		n >>= 1;
	}
	return count;
}
*/
int GetNumber2(int n)
{
	int count = 0;
	unsigned int flag = 1;
	while(flag)
	{
		if(n & flag)
		{
			count++;
		}
		flag <<= 1;//将1一直左移，而不是将n右移，第一次n&0001 第二次n&0010
	}
	return count;
}
//整数除以2和右移1位在数学上是等价的，但是除法的效率比移位运算要低的多


int GetNumber3(int n)
{
	int count = 0;
	while(n)
	{
		count++;
		n &= (n-1);//把二进制n中最右边的1去掉
	}
	return count;
}

对常用的位运算进行总结

//位运算实现加减乘除
#include<stdio.h>
#include<math.h>

//不用加减乘除号求两个数之和
int Sum(int num1,int num2)
{
	int tmp1 = 0;
	int tmp2 = 0;
	do
	{
		tmp1 = num1 ^ num2;
		tmp2 = (num1 & num2) << 1;

		num1 = tmp1;
		num2 = tmp2;
	}
	while(tmp2 != 0);

	return tmp1;
}

//不用加减乘除号求两个数之差
int Sub(int num1,int num2)
{
	num2 = -num2;
	return Sum(num1,num2);
}
//不用加减乘除号求两个数之积
int Multi(int num1,int num2)
{
	int sum = 0;
	if(num1 < 0 && num2 < 0)
	{
		for(int i = 0; i < -num2; ++i)
		{
			sum = Sum(sum,-num1);
		}
		return sum;
	}
	if(num1 > 0 && num2 < 0)
	{
		int tmp = num1;
		num1 = num2;
		num2 = tmp;
	}
	for(int i = 0; i < num2; ++i)
	{
		sum = Sum(sum,num1);
	}
	return sum;
}
//不用加减乘除号求两个数之商
bool Div(int num1,int num2,int*p)
{
	*p = 0;
	if(num2 == 0)
	{
		return false;
	}
	else if(abs(num1) < abs(num2) || num1 == 0)
	{
		*p = 0;
		return true;
	}
	else
	{
		if(num1 > 0 && num2 > 0)
		{
			while(num1 > num2)
			{
				(*p)++;
				num1 = Sub(num1,num2);
			}
		}
		else if(num1 < 0 || num2 < 0)
		{
			num1 = abs(num1);
			num2 = abs(num2);
			while(num1 > num2)
			{
				(*p)++;
				num1 = Sub(num1,num2);
			}
			(*p) = -(*p);
		}
		else
		{
			num1 = abs(num1);
			num2 = abs(num2);
			while(num1 > num2)
			{
				(*p)++;
				num1 = Sub(num1,num2);
			}
		}
	}
	return true;
}