题意:
有n个有标号的盒子和m种有标号的球,每种球有a[i]个,求每个盒子至少放一种球的总方案数。
分析:
我们可以先考虑--把每个a[i]分到n个盒子里(允许有空盒)那么方案数为![\textrm{C}_{n+a[i]-1}^{n-1}](https://latex.csdn.net/eq?%5Ctextrm%7BC%7D_%7Bn+a%5Bi%5D-1%7D%5E%7Bn-1%7D) ,根据乘法原理方案数
,根据乘法原理方案数![\prod _{i=1}^{m}\textrm{C}_{n+a[i]-1}^{n-1}](https://latex.csdn.net/eq?%5Cprod%20_%7Bi%3D1%7D%5E%7Bm%7D%5Ctextrm%7BC%7D_%7Bn+a%5Bi%5D-1%7D%5E%7Bn-1%7D) 当然这样想使不完全正确的,其中包含有人没有的情况;不合法的情况为K[i];(i表示至少有i个盒子为空)(范围从i到n-1,上一步求出必有一人有);即我们要求出看k[x]=
当然这样想使不完全正确的,其中包含有人没有的情况;不合法的情况为K[i];(i表示至少有i个盒子为空)(范围从i到n-1,上一步求出必有一人有);即我们要求出看k[x]= ![\textrm{C}_{n+a[i]-1}^{n-x-1}](https://latex.csdn.net/eq?%5Ctextrm%7BC%7D_%7Bn+a%5Bi%5D-1%7D%5E%7Bn-x-1%7D) (也就是求出将a[i]个球放入n-x个盒子中);但是因为k[i]
(也就是求出将a[i]个球放入n-x个盒子中);但是因为k[i]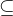 k[j](i<j)所以容斥一下;
k[j](i<j)所以容斥一下; ![\sum^{n-1}_{i=0}(-1)^i\prod^m_{j=1}C(n\!+\!a[j]\!-\!i\!-\!1,n\!-\!i\!-\!1\!)](https://latex.csdn.net/eq?%5Csum%5E%7Bn-1%7D_%7Bi%3D0%7D%28-1%29%5Ei%5Cprod%5Em_%7Bj%3D1%7DC%28n%5C%21+%5C%21a%5Bj%5D%5C%21-%5C%21i%5C%21-%5C%211%2Cn%5C%21-%5C%21i%5C%21-%5C%211%5C%21%29)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
ll n,m,te[1010],C[2010][2010];
int main()
{
freopen("speciall.in","r",stdin);
freopen("speciall.out","w",stdout);
C[0][0]=1;
for(int i=1;i<=2005;i++)
{
C[i][0]=1;
for(int j=1;j<=i;j++)
{
C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
}//预处理
scanf("%lld%lld",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%lld",&te[i]);
}
ll ans=0;
for(int i=0;i<n;i++)
{
ll t=C[n][i];
for(int j=1;j<=m;j++)
{
t=t*C[te[j]+n-i-1][n-i-1]%mod;
}
if(i&1) ans=(ans-t+mod)%mod;
else ans=(ans+mod+t)%mod;
}
printf("%lld",(ans+mod)%mod);
}
![\textrm{C}_{n+a[i]-1}^{n-1}](https://latex.csdn.net/eq?%5Ctextrm%7BC%7D_%7Bn+a%5Bi%5D-1%7D%5E%7Bn-1%7D) ,根据乘法原理方案数
,根据乘法原理方案数![\prod _{i=1}^{m}\textrm{C}_{n+a[i]-1}^{n-1}](https://latex.csdn.net/eq?%5Cprod%20_%7Bi%3D1%7D%5E%7Bm%7D%5Ctextrm%7BC%7D_%7Bn+a%5Bi%5D-1%7D%5E%7Bn-1%7D) 当然这样想使不完全正确的,其中包含有人没有的情况;不合法的情况为K[i];(i表示至少有i个盒子为空)(范围从i到n-1,上一步求出必有一人有);即我们要求出看k[x]=
当然这样想使不完全正确的,其中包含有人没有的情况;不合法的情况为K[i];(i表示至少有i个盒子为空)(范围从i到n-1,上一步求出必有一人有);即我们要求出看k[x]= ![\textrm{C}_{n+a[i]-1}^{n-x-1}](https://latex.csdn.net/eq?%5Ctextrm%7BC%7D_%7Bn+a%5Bi%5D-1%7D%5E%7Bn-x-1%7D) (也就是求出将a[i]个球放入n-x个盒子中);但是因为k[i]
(也就是求出将a[i]个球放入n-x个盒子中);但是因为k[i]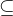 k[j](i<j)所以容斥一下;
k[j](i<j)所以容斥一下; ![\sum^{n-1}_{i=0}(-1)^i\prod^m_{j=1}C(n\!+\!a[j]\!-\!i\!-\!1,n\!-\!i\!-\!1\!)](https://latex.csdn.net/eq?%5Csum%5E%7Bn-1%7D_%7Bi%3D0%7D%28-1%29%5Ei%5Cprod%5Em_%7Bj%3D1%7DC%28n%5C%21+%5C%21a%5Bj%5D%5C%21-%5C%21i%5C%21-%5C%211%2Cn%5C%21-%5C%21i%5C%21-%5C%211%5C%21%29)






















 283
283











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








