写在前面:
前面我们讲的数据结构都是针对于一对一或一对多的情形,如果涉及到多对多的复杂情况就要用到我们接下来讲解的图了,这一讲我们重点讲解邻接表、邻接矩阵、十字链表以及邻接多重表的代码实现。如果已经对图的概念比较熟悉的小伙伴,可以拉到下面看相关的代码实现。
图的概述
图 G 是由两个集合 V 和 E 组成,记为 G = (V,E),其中 V 代表顶点,E 代表边,如下图(这里涉及到有向边和无向边,下面会展开讲)。
图的相关概念
简单图
在图结构中,若不存在顶点到其自身的边,且同⼀条边没有重复出现,则称这样的图为简单图。
无向图
在图 G 中,如果代表边的顶点偶对是无序的,则称 G 为无向图,也就是上图没有箭头的边组成的。
有向图
在图 G 中,如果表示边的顶点偶对是有序的,则称 G 为有向图。⼀个图要么为无向图,要么为有向图。不存在部分有向或者部分无向的情况(上图只是作为一个例子)。
完全图
如果图中的每两个顶点之间,都存在一条边,我们就称这个图为完全图。
- 完全有向图:有 n(n-1) 条边
- 完全无向图:有 n(n-1)/2 条边
端点和邻接点
在一个无向图中,若存在一条边(i,j),则称顶点 i 和顶点 j 为该边的两个端点,并称它们互为邻接点。
在一个有向图中,若存在一条边 <i,j> ,则称顶点 i 和顶点 j 为该边的两个端点,它们互为邻接点。此时,顶点 i 为起点。顶点 j 为终点。
顶点的度、入度和出度
在无向图中,顶点所具有的边的数目称为该顶点的度。
在有向图中,顶点 v 的度就分为入度和出度,以顶点 v 为终点的入边的数目,称为该顶点的入度。以顶点 v 为起点的出边的数目,称为该顶点的出度。一个顶点的入度和出度的和称为该顶点的度。在一个具有 e 条边的图中:度之和为 2e 。
子图
设有两个图 G =(V,E)和 G’ =(V’ , E’),若 V’ 是 V 的子集。则称 G’ 是 G 的子图。
回路或环
如果一条路径上的开始点与结束点为同一个顶点,则称此路为回路或者为环。开始点和结束点相同的简单路径被称为简单回路或者简单环。
如果经过图中各边一次且恰好一次的环路,称之为欧拉环路,也就是其长度恰好等于图中边的总数,{C,A,B,A,D,C,D,B,C} 就是一条欧拉环路。
如果是经过图中的各顶点一次且恰好一次的环路,称作哈密尔顿环路,其长度等于构成环路的边数。{C,A,D,B,C} 就是一条哈密尔顿环路。

连通、连通图和连通分量
在无向图 G 中,若从顶点 i 到顶点 j 有路径,则称这两个顶点时连通的。如果图 G 中任意两个顶点都连通,则称 G 为连通图,否则称为非连通图。无向图 G 中的极大连通子图称为 G 的连通分量。对于连通图只有一个极大连通子图,就是它本身(是唯一的)。非连通图有多个极大连通子图。(非连通图的极大连通子图叫做连通分量,每个分量都是一个连通图)。之所以称为极大是因为如果此时加入一个不在图的点集中的点都会导致它不再连通。
至于极小连通子图,首先只有连通图才有极小连通子图这个概念。就像一个四边形,四个节点四条边,其实三条边就能连通了,所以四个节点三条边,就 OK 了,就是在能连通的前提下,把多余的边去掉。
强连通图和强连通分量
在有向图 G 中,若从顶点 i 到顶点 j 有路径,则称从顶点 i 到顶点 j 是连通的。若图 G 中的任意两个顶点 i 和顶点 j 都连通,即从顶点 i 到顶点 j 和从顶点 j 到顶点 i 都存在路径,则称图 G 是强连通图。有向图 G 中的极大强连通子图称为 G 的强连通分量。显然,强连通图只有一个强连通分量,即自身,非强连通图有多个强连通分量。
稠密图、稀疏图
当一个图接近完全图的时候,称之为稠密图;相反,当一个图含有较少的边数,则称之为稀疏图。
一般对于这个边的个数,说法比较多,通常认为边小于 nlogn(n 是顶点的个数)的图称之为稀疏图,反之称为稠密图。
权和网
图中的每一条边都可以附有一个对应的数,这种与边相关的数称为权。权可以表示从一个顶点到另一个顶点的距离或者花费的代价。边上带有权的图称为带权图,也称之为网。
连通图的生成树
所谓连通图的生成树是一个极小的连通子图,它含有图中全部的 n 个结点,但是只有构成树的 n-1 条边。
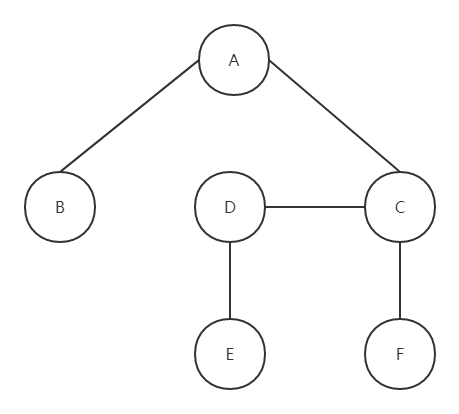
图的存储结构
图在内存中存储方式有很多种,最经典的包括邻接矩阵、邻接表、十字链表和邻接多重表。接下来,我将会讲解具体的实现方式。
邻接矩阵
无向图邻接矩阵
图的邻接矩阵是用两个数组来表示,一个一位数组存储图中的顶点信息,一个二维数组(我们将这个数组称之为邻接矩阵)存储图中的边的信息。

| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 1 | 0 |
| B | 1 | 0 | 0 | 1 |
| C | 1 | 0 | 0 | 1 |
| D | 0 | 1 | 1 | 0 |
通过观察可以发现,这个邻接矩阵对于对角线是对称的,所以如果我们只是存储无向边的话,就有点浪费空间了。
有向图邻接矩阵
这里和无向图就不一样了,邻接矩阵就不会每次都是对称的。
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 0 |
| C | 1 | 0 | 0 | 0 |
| D | 0 | 1 | 1 | 0 |

另外有向图是有讲究的,要考虑入度和出度,顶点 A 的入度为 2 ,正好是第 1 列的各数之和,顶点 A 的出度为1 ,正好是第 1 行的各数之和。
带权图的邻接矩阵
带权图中的每一条边上带有权值,邻接矩阵中的值则为权值,当两个顶点之间没有边时,则用无穷大表示。
| A | B | C | D | |
|---|---|---|---|---|
| A | ∞ | 3 | ∞ | ∞ |
| B | 5 | ∞ | ∞ | ∞ |
| C | 4 | ∞ | ∞ | ∞ |
| D | ∞ | 1 | 2 | ∞ |

我们这里就来实现以下带权有向图的邻接矩阵的代码,这里实现代码中用的是数字表示结点信息,节点自身权值为 -1 ,无边权值为 0 ,并且是以 出度结点 | 入度结点 | 权值 的形式输入每条边。
有向图代码
#include <bits/stdc++.h>
using namespace std;
#define MaxVertices 100 //假设包含的最大结点数
#define MaxWeight -1 //假设两点不邻接的正无穷值
//定义结点
struct AdjMarix {
int Vertices[MaxVertices]; //存储结点信息
int Edge[MaxVertices][MaxVertices] = { 0 }; //存储每条边的权值
int numV; //当前顶点的个数
int numE; //当前边的个数
};
void CreatGraph(AdjMarix *G) {
int vi, vj, w;
cout << "请输入顶点数量:" << endl;
cin >> G->numV;
cout << "请输入顶点信息:" << endl;
//输入结点的编号并初始化
for (int i = 0; i < G->numV; i++) {
cin >> vi;
G->Vertices[i] = vi;
G->Edge[i][i] = MaxWeight;
}
cout << "请输入边的数量:" << endl;
cin >> G->numE;
cout << "请输入边的信息:" << endl;
for (int i = 0; i < G->numE; i++) {
cin >> vi >> vj >> w;
G->Edge[vi - 1][vj - 1] = w;
//G->Edge[vj-1][vi-1]=w; 无向图需要再加上这一句
}
}
//遍历图
void ShowGraph(AdjMarix *G) {
for (int i = 0; i < G->numV; i++) {
for (int j = 0; j < G->numV; j++) {
cout << G->Edge[i][j] << " ";
}
cout << endl;
}
}
int main() {
AdjMarix AM;
CreatGraph(&AM);
ShowGraph(&AM);
}

邻接表
这个时候我们会发现一个问题,就是空间浪费问题。尤其是面对边数相对比较少的稀疏图来说,这种结构无疑是存在对存储空间的极大浪费。
因此我们可以考虑另外一种存储结构方式,例如把数组与链表结合在一起来存储,这种方式在图结构也适用,我们称为邻接表。
如下图所示,用一个数组来存储所有结点信息,然后每个结点都有一个指出去的指针,指向该结点到其它结点。

有向图代码
#include <bits/stdc++.h>
using namespace std;
#define MaxVertices 100
//定义结点
struct VertexNode {
int data; //结点编号
int weight = 0; //指向下一个结点的边的权值
VertexNode *next = NULL;
};
//定义邻接表
struct GraphAdjList {
VertexNode *AdjList[MaxVertices]; //存储所有结点
int numV, numE;
};
//创建图
void CreatGraph(GraphAdjList &G) {
int vi, vj, w;
cout << "请输入顶点数:" << endl;
cin >> G.numV;
cout << "请输入顶点信息:" << endl;
for (int i = 0; i < G.numV; i++) {
cin >> vi;
VertexNode *new_node = new VertexNode;
new_node->data = vi;
G.AdjList[i] = new_node;
}
cout << "请输入边的数量:" << endl;
cin >> G.numE;
cout << "请输入边的信息:" << endl;
for (int i = 0; i < G.numE; i++) {
cin >> vi >> vj >> w;
//找到邻接表中对应结点的位置,往其中链表插入对应边
for (int j = 0; j < G.numV; j++) {
if (vi == G.AdjList[j]->data) {
VertexNode *temp = G.AdjList[j];
//这里用的是尾插法
while (temp->next != NULL) {
temp = temp->next;
}
VertexNode *newEdge = new VertexNode;
newEdge->data = vj;
newEdge->weight = w;
temp->next = newEdge;
break;
}
}
}
}
//遍历图
void showGraph(GraphAdjList &G) {
for (int i = 0; i < G.numV; i++) {
VertexNode *temp = G.AdjList[i]->next;
int vi = G.AdjList[i]->data;
cout << "顶点" << vi << "的边有:" << endl;
if (temp == NULL) {
cout << "无" << endl;
}
while (temp != NULL) {
cout << vi << "->" << temp->data << " 权值=" << temp->weight << endl;
temp = temp->next;
}
}
}
int main() {
GraphAdjList GAL;
CreatGraph(GAL);
showGraph(GAL);
}

逆邻接表
逆邻接表其实和邻接表十分相像,邻接表是用来存储出度的指针,而逆邻接表就是用来存储入度的指针。
十字链表
十字链表实质上就是将邻接表和逆邻接表结合起来了,直接用一个数组表示。
顶点集:

边集:

其中的 tailVex 表示该弧的弧尾顶点在顶点数组中的位置,headVex 表示该弧的弧头顶点在顶点数组中的位置。hLink 则表示指向弧头相同的下一条弧,tLink 则表示指向弧尾相同的下一条弧。
我们这里定义的是没有箭头的是弧尾,有箭头的是弧头。

这里比较难理解的是 firstIn ,headLink 把所有弧头相同的边连了起来,比如指向结点 V0 的边有两条,分别是 V1 -> V0 和 V3 -> V0,所以从 V0 的 firstIn 连出去,先指向第一条边 1 -> 0 ,再将 1 -> 0 的 headLink 指向下一条也是指向 V0 的边。同样,V1 和 V3 的 firstIn 也是一样,V2 没有连是因为没有指向 V2 的边。
有向图代码
#include <bits/stdc++.h>
using namespace std;
//边集定义
struct ArcBox {
int headvex, tailvex; //对应弧头和弧尾的下标
ArcBox *hlink, * tlink; //分别指向弧头相同和弧尾相同的下标
};
//顶点定义
struct VexNode {
int data;
ArcBox *firstin, *firstout;
};
//定义图
struct OLGraph {
VexNode xlist[100];
int vexnum, arcnum;
};
//找到顶点在数组中的位置
int Location(OLGraph *G, int key) {
//遍历每个顶点
for (int i = 0; i < G->vexnum; i++) {
if (key == G->xlist[i].data) {
return i;
}
}
}
//创建图
void CreatGraph(OLGraph *G) {
int vi, vj, xi, xj;
cout << "请输入顶点数:" << endl;
cin >> G->vexnum;
cout << "请输入顶点信息:" << endl;
for (int i = 0; i < G->vexnum; i++) {
cin >> G->xlist[i].data;
G->xlist[i].firstin = NULL;
G->xlist[i].firstout = NULL;
}
cout << "请输入弧数:" << endl;
cin >> G->arcnum;
cout << "请输入弧的信息:" << endl;
for (int i = 0; i < G->arcnum; i++) {
cin >> vi >> vj;
xi = Location(G, vi);
xj = Location(G, vj);
ArcBox *new_node = new ArcBox;
new_node->headvex = xj; //headvex是存有箭头的弧头
new_node->tailvex = xi; //tailvex是存没有箭头的弧尾
new_node->hlink = G->xlist[xj].firstin; //将hlink指向弧头也是xj的边
new_node->tlink = G->xlist[xi].firstout; //将tlink指向弧尾也是xi的边
G->xlist[xj].firstin = G->xlist[xi].firstout = new_node; //更新firstin和firstout
}
}
//遍历图
void ShowGraph(OLGraph *G) {
for (int i = 0; i < G->vexnum; i++) {
int vi = G->xlist[i].data;
cout << "与结点" << vi << "相连的结点有:" << endl;
ArcBox *temp = G->xlist[i].firstout;
cout << "【出度】" << endl;
if (temp == NULL) {
cout << "暂无";
}
while (temp != NULL) {
cout << vi << "->" << G->xlist[temp->headvex].data << " ";
temp = temp->tlink;
}
temp = G->xlist[i].firstin;
cout << endl << "【入度】" << endl;
if (temp == NULL) {
cout << "暂无";
}
while (temp != NULL) {
cout << G->xlist[temp->tailvex].data << "->" << vi << " ";
temp = temp->hlink;
}
cout << endl;
}
}
int main() {
OLGraph OLG;
CreatGraph(&OLG);
ShowGraph(&OLG);
}


邻接多重表
由于十字链表对于边的改动十分麻烦,所以就有了邻接多重表。它在十字链表的边集定义上做了一些改动,同时在顶点数组中只用保留一个指针。
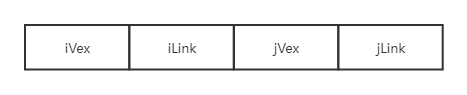
其中 iVex 和 jVex 是与某条边依附的两个顶点在顶点表中的下标。iLink 指向依附顶点 iVex 的下一条边,jLink 指向依附顶点 jVex 的下一条边。

这每条边中每个结点后面的指针其实就是指向下一个包含该结点的边。
#include <bits/stdc++.h>
using namespace std;
//定义边集
struct ArcNode {
int ivex, jvex;
ArcNode *vi, * vj;
};
//定义顶点
struct VexNode {
int data;
ArcNode *firstEdge;
};
//定义图
struct Graph {
VexNode Dvex[100];
int vexnum, arcnum;
};
//找到顶点在数组中的下标
int Location(Graph *G, int key) {
for (int i = 0; i < G->vexnum; i++) {
if (G->Dvex[i].data == key) {
return i;
}
}
}
//创建图
void CreatGraph(Graph *G) {
int vi, vj;
cout << "请输入顶点数:" << endl;
cin >> G->vexnum;
cout << "请输入顶点信息:" << endl;
for (int i = 0; i < G->vexnum; i++) {
cin >> G->Dvex[i].data;
G->Dvex[i].firstEdge = NULL;
}
cout << "请输入边数:" << endl;
cin >> G->arcnum;
cout << "请输入边的信息:" << endl;
for (int i = 0; i < G->arcnum; i++) {
cin >> vi >> vj;
ArcNode *new_edge = new ArcNode;
int xi = Location(G, vi);
int xj = Location(G, vj);
new_edge->ivex = xi; //记录弧尾即不带箭头的一边
new_edge->jvex = xj; //记录弧头即带箭头的一边
new_edge->vi = G->Dvex[xi].firstEdge; //指向包含vi的边
new_edge->vj = G->Dvex[xj].firstEdge; //指向包含vj的边
G->Dvex[xi].firstEdge = G->Dvex[xj].firstEdge = new_edge; //更新firstEdge
}
}
//遍历图
void showGraph(Graph *G) {
for (int i = 0; i < G->vexnum; i++) {
int vi = G->Dvex[i].data;
ArcNode *temp = G->Dvex[i].firstEdge;
cout << "与结点" << vi << "相连的结点有:" << endl;
if (temp == NULL) {
cout << "暂无";
}
while (temp != NULL) {
int vj, flag = 0;
if (G->Dvex[temp->ivex].data == vi) {
vj = G->Dvex[temp->jvex].data;
flag = 1;
} else {
vj = G->Dvex[temp->ivex].data;
}
cout << "结点" << vj << " ";
if (flag == 1) {
temp = temp->vi;
} else {
temp = temp->vj;
}
}
cout << endl;
}
}
int main() {
Graph G;
CreatGraph(&G);
showGraph(&G);
}

如果大家有什么问题的话,欢迎在下方评论区进行讨论哦~
























 1300
1300

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








