Intersection
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 9464 | Accepted: 2494 |
Description
You are to write a program that has to decide whether a given line segment intersects a given rectangle.
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)
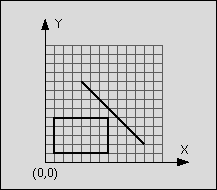
Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)

Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
Input
The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format:
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
Output
For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.
Sample Input
1 4 9 11 2 1 5 7 1
Sample Output
F
Source
这里考察的就是简单的几何知识在计算机中的运用,此处需要用到的就是判断两线段是否相交,这里要运用叉积,假设有两条线段a,b;
1.a x b>0, 则表明b在a的顺时针方向;
2.a x b<0, 则表明b在a的逆时针方向;
3.a x b=0, 则表明a,b在一条直线上;
以此为基础我们就可以判断两线段是否相交啦,具体思路如下:
先用一条线段a的一端为公共点,再取另一条线段b一端点,连接,得到两条具有公共点直线,有上面知识判断方向,然后再取b另一端点连成直线再判断方向,如前后所得两直线相对于a的方向不同,则代表线段b横跨啦线段a所在的直线,同样以此推理,如果线段a也横框线段b所在直线,则两线段相互横跨,则必定相交;代码具体如下:
#include<stdio.h>
#include<stdlib.h>
#define max(m,n)(m>n?m:n)
#define min(m,n)(m<n?m:n)
int inrectangle(double x,double y,double x1,double y1,double x2,double y2){//判断点是否在矩形内
if(min(x1,x2)<=x&&x<=max(x1,x2)&&min(y1,y2)<=y&&y<=max(y1,y2))
return 1;
else
return 0;
}
double direct(double x,double y,double x1,double y1,double x2,double y2){//判断以(x1,y1)为公共点,与其他两点所构成线段的位置
return (x1-x)*(y1-y2)-(x1-x2)*(y1-y);
}
int intersect(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//判断两直线是否相交
if(direct(x1,y1,x3,y3,x4,y4)*direct(x2,y2,x3,y3,x4,y4)<0&&direct(x3,y3,x1,y1,x2,y2)*direct(x4,y4,x1,y1,x2,y2)<0)//此处为两线段相互跨立对方则相交的情况
return 1;
else if(direct(x1,y1,x3,y3,x4,y4)==0&&inrectangle(x1,y1,x3,y3,x4,y4))//剩下的均为有一点在任意一条直线上的情况
return 1;
else if(direct(x2,y2,x3,y3,x4,y4)==0&&inrectangle(x2,y2,x3,y3,x4,y4))
return 1;
else if(direct(x3,y3,x1,y1,x2,y2)==0&&inrectangle(x3,y3,x1,y1,x2,y2))
return 1;
else if(direct(x4,y4,x1,y1,x2,y2)==0&&inrectangle(x4,y4,x1,y1,x2,y2))
return 1;
else //不满足的则证明不相交
return 0;
}
int main(){
double x1,x2,x3,x4,y1,y2,y3,y4;
int n,i,flag=0;
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%lf %lf %lf %lf %lf %lf %lf %lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
if(min(x3,x4)<x1&&x1<max(x3,x4)&&min(y3,y4)<y1&&y1<max(y3,y4))//点在矩形内
flag=1;
else if(x3<x2&&x2<x4&&y4<y2&&y2<y3)
flag=1;
else if(intersect(x1,y1,x2,y2,x3,y3,x3,y4)==1)
flag=1;
else if(intersect(x1,y1,x2,y2,x3,y3,x4,y3)==1)
flag=1;
else if(intersect(x1,y1,x2,y2,x3,y4,x4,y4)==1)
flag=1;
else if(intersect(x1,y1,x2,y2,x4,y3,x4,y4)==1)
flag=1;
if(flag==1)
printf("T\n");
else
printf("F\n");
flag=0;
}
system("pause");
return 0;
}
#include<stdlib.h>
#define max(m,n)(m>n?m:n)
#define min(m,n)(m<n?m:n)
int inrectangle(double x,double y,double x1,double y1,double x2,double y2){//判断点是否在矩形内
if(min(x1,x2)<=x&&x<=max(x1,x2)&&min(y1,y2)<=y&&y<=max(y1,y2))
return 1;
else
return 0;
}
double direct(double x,double y,double x1,double y1,double x2,double y2){//判断以(x1,y1)为公共点,与其他两点所构成线段的位置
return (x1-x)*(y1-y2)-(x1-x2)*(y1-y);
}
int intersect(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4){//判断两直线是否相交
if(direct(x1,y1,x3,y3,x4,y4)*direct(x2,y2,x3,y3,x4,y4)<0&&direct(x3,y3,x1,y1,x2,y2)*direct(x4,y4,x1,y1,x2,y2)<0)//此处为两线段相互跨立对方则相交的情况
return 1;
else if(direct(x1,y1,x3,y3,x4,y4)==0&&inrectangle(x1,y1,x3,y3,x4,y4))//剩下的均为有一点在任意一条直线上的情况
return 1;
else if(direct(x2,y2,x3,y3,x4,y4)==0&&inrectangle(x2,y2,x3,y3,x4,y4))
return 1;
else if(direct(x3,y3,x1,y1,x2,y2)==0&&inrectangle(x3,y3,x1,y1,x2,y2))
return 1;
else if(direct(x4,y4,x1,y1,x2,y2)==0&&inrectangle(x4,y4,x1,y1,x2,y2))
return 1;
else //不满足的则证明不相交
return 0;
}
int main(){
double x1,x2,x3,x4,y1,y2,y3,y4;
int n,i,flag=0;
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%lf %lf %lf %lf %lf %lf %lf %lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
if(min(x3,x4)<x1&&x1<max(x3,x4)&&min(y3,y4)<y1&&y1<max(y3,y4))//点在矩形内
flag=1;
else if(x3<x2&&x2<x4&&y4<y2&&y2<y3)
flag=1;
else if(intersect(x1,y1,x2,y2,x3,y3,x3,y4)==1)
flag=1;
else if(intersect(x1,y1,x2,y2,x3,y3,x4,y3)==1)
flag=1;
else if(intersect(x1,y1,x2,y2,x3,y4,x4,y4)==1)
flag=1;
else if(intersect(x1,y1,x2,y2,x4,y3,x4,y4)==1)
flag=1;
if(flag==1)
printf("T\n");
else
printf("F\n");
flag=0;
}
system("pause");
return 0;
}
























 620
620

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








