CUDA入门之采用shared memory优化矩阵乘法（二）

还能再吃一碗w

已于 2022-07-09 23:17:57 修改

阅读量647

点赞数 1

CC 4.0 BY-SA版权

分类专栏： CUDA入门文章标签：矩阵算法线性代数

于 2022-07-08 10:10:13 首次发布

本文链接：https://blog.csdn.net/Not_answer/article/details/125669186

CUDA入门专栏收录该内容

6 篇文章

订阅专栏

参加CUDA On Arm Platform 线上夏令营学习笔记（二）

优化思路
代码部分
讲解部分
实验结果比较

优化思路

CUDA入门之采用shared memory优化矩阵乘法（一）
中讲解了基础的利用Shared Memory优化矩阵乘法，在其中，申请的Shared Memory的形状为正方形，且大小等同于block的大小。
可以考虑一下，同样为上一篇博客中所举得1616的C = MN的矩阵例子，对应于矩阵M的Shared memory一直是沿着行来滑动，而对应于矩阵N的shared memory一直是沿着列来滑动，如果将对应于矩阵M的Shared memory的形状从正方形改为行数较小而列数较大的形状，对应于矩阵N的shared memory改为列数较小而行数较大的情况，将大大减少滑块滑动的次数，可以减少核函数的运行时间，从而提高矩阵乘法的执行速度。

代码部分

#include <stdio.h>
#include <math.h>
#include "error.cuh"

#define BLOCK_SIZE 32

__global__ void gpu_matrix_mult_shared(int *d_a, int *d_b, int *d_result, int m, int n, int k){
    __shared__ int tile_a[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ int tile_b[BLOCK_SIZE][BLOCK_SIZE];
    
    int row = blockIdx.y * BLOCK_SIZE + threadIdx.y;
    int col = blockIdx.x * BLOCK_SIZE + threadIdx.x;
    int tmp = 0;
    int idx;
    
    for(int sub = 0; sub <= n/BLOCK_SIZE; ++sub){
        idx = row * n + sub * BLOCK_SIZE + threadIdx.x;
        tile_a[threadIdx.y][threadIdx.x] = row < m &&(sub * BLOCK_SIZE + threadIdx.x)<n?d_a[idx]:0;
        idx = (sub * BLOCK_SIZE + threadIdx.y) * k + col;
        tile_b[threadIdx.y][threadIdx.x] = col<k && (sub * BLOCK_SIZE + threadIdx.y)<n? d_b[idx]:0;
        
        __syncthreads();
        for(int i = 0; i < BLOCK_SIZE; ++i){
            tmp+= tile_a[threadIdx.y][i] * tile_b[i][threadIdx.x];
        }
        __syncthreads();
    }
    if(row < m && col < k){
        d_result[row * k + col] = tmp;
    }
}
__global__ void gpu_matrix_mult_test(int *a, int *b, int *c, int m, int n, int k){
    __shared__ int tile_a[BLOCK_SIZE/2][BLOCK_SIZE*2];
    __shared__ int tile_b[BLOCK_SIZE*2][BLOCK_SIZE/2];
    
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    int tmp = 0;
    int idx1, idx2,idx3, idx4;
    
    for(int sub = 0; sub<= n/BLOCK_SIZE/2; ++sub){
        idx1 = row * n + sub * BLOCK_SIZE*2 + threadIdx.x;
        idx2 = row * n + sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.x;
        idx3 = row * n + sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.x;
        idx4 = row * n + sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.x;
        
        tile_a[threadIdx.y][threadIdx.x] = row < m &&(sub * BLOCK_SIZE*2 + threadIdx.x)<n?a[idx1]:0;
        tile_a[threadIdx.y][threadIdx.x + BLOCK_SIZE/2] = row < m &&(sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.x)<n?a[idx2]:0;
        tile_a[threadIdx.y][threadIdx.x + BLOCK_SIZE] = row < m &&(sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.x)<n?a[idx3]:0;
        tile_a[threadIdx.y][threadIdx.x + BLOCK_SIZE*3/2] = row < m &&(sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.x)<n?a[idx4]:0;
        
        idx1 = (sub * BLOCK_SIZE*2 + threadIdx.y) * k + col;
        idx2 = (sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.y) * k + col;
        idx3 = (sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.y) * k + col;
        idx4 = (sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.y) * k + col;
        
        tile_b[threadIdx.y][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + threadIdx.y)<n? b[idx1]:0;
        tile_b[threadIdx.y + BLOCK_SIZE/2][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.y)<n? b[idx2]:0;
        tile_b[threadIdx.y + BLOCK_SIZE][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.y)<n? b[idx3]:0;
        tile_b[threadIdx.y + BLOCK_SIZE*3/2][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.y)<n? b[idx4]:0;
        
        __syncthreads();
        for(int i = 0; i < BLOCK_SIZE*2; ++i){
            tmp+= tile_a[threadIdx.y][i] * tile_b[i][threadIdx.x];
        }
        __syncthreads();
    }
    if(row < m && col < k){
        c[row * k + col] = tmp;
    }
}

int main(int argc, char const *argv[])
{
    int m=1600;
    int n=1007;
    int k=1600;

    int *h_a, *h_b, *h_c, *h_cc, *h_cs;
    CHECK(cudaMallocHost((void **) &h_a, sizeof(int)*m*n));
    CHECK(cudaMallocHost((void **) &h_b, sizeof(int)*n*k));
    CHECK(cudaMallocHost((void **) &h_c, sizeof(int)*m*k));
    CHECK(cudaMallocHost((void **) &h_cc, sizeof(int)*m*k));
    CHECK(cudaMallocHost((void **) &h_cs, sizeof(int)*m*k));
    
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            h_a[i * n + j] = 3;
        }
    }

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < k; ++j) {
            h_b[i * k + j] =2;
        }
    }

    int *d_a, *d_b, *d_c, *d_c_share;
    CHECK(cudaMalloc((void **) &d_a, sizeof(int)*m*n));
    CHECK(cudaMalloc((void **) &d_b, sizeof(int)*n*k));
    CHECK(cudaMalloc((void **) &d_c, sizeof(int)*m*k));
    CHECK(cudaMalloc((void **) &d_c_share, sizeof(int)*m*k));
    
    cudaEvent_t start, stop,stop_share;
    CHECK(cudaEventCreate(&start));
    CHECK(cudaEventCreate(&stop));
    CHECK(cudaEventCreate(&stop_share));

    CHECK(cudaMemcpy(d_a, h_a, sizeof(int)*m*n, cudaMemcpyHostToDevice));
    CHECK(cudaMemcpy(d_b, h_b, sizeof(int)*n*k, cudaMemcpyHostToDevice));
    CHECK(cudaEventRecord(start));
    //cudaEventQuery(start);
    unsigned int grid_rows2 = (m + BLOCK_SIZE - 1) / BLOCK_SIZE;
    unsigned int grid_cols2 = (k + BLOCK_SIZE - 1) / BLOCK_SIZE;
    dim3 dimGrid2(grid_cols2, grid_rows2);
    dim3 dimBlock2(BLOCK_SIZE, BLOCK_SIZE);
    
    gpu_matrix_mult_shared<<<dimGrid2, dimBlock2>>>(d_a, d_b, d_c_share, m,n,k);
    CHECK(cudaMemcpy(h_cs, d_c_share, (sizeof(int)*m*k), cudaMemcpyDeviceToHost));
    
    CHECK(cudaEventRecord(stop));
    CHECK(cudaEventSynchronize(stop));
    
    unsigned int grid_rows1 = (m + BLOCK_SIZE - 1) / (BLOCK_SIZE / 2);
    unsigned int grid_cols1 = (k + BLOCK_SIZE - 1) / (BLOCK_SIZE / 2);
    dim3 dimGrid1(grid_cols1, grid_rows1);
    dim3 dimBlock1(BLOCK_SIZE/2, BLOCK_SIZE/2);
    
    gpu_matrix_mult_test<<<dimGrid1, dimBlock1>>>(d_a, d_b, d_c, m, n, k);
    CHECK(cudaMemcpy(h_c, d_c, (sizeof(int)*m*k), cudaMemcpyDeviceToHost));
     
    CHECK(cudaEventRecord(stop_share));
    CHECK(cudaEventSynchronize(stop_share));
    
    float elapsed_time, elapsed_time_share;
    CHECK(cudaEventElapsedTime(&elapsed_time,start,stop));
    CHECK(cudaEventElapsedTime(&elapsed_time_share, stop, stop_share));
    printf("Time = %g ms.\n", elapsed_time);
    printf("Time_share = %g ms.\n", elapsed_time_share);
    
    CHECK(cudaEventDestroy(start));
    CHECK(cudaEventDestroy(stop));
    CHECK(cudaEventDestroy(stop_share));
    


    int ok = 1;
    for (int i = 0; i < m; ++i)
    { 
        for (int j = 0; j < k; ++j)
        {
            if(fabs(h_cs[i*k + j] - h_c[i*k + j])>(1.0e-10))
            {
                ok = 0;
            }
        }
    }

    if(ok)
    {
        printf("Pass!!!\n");
    }
    else
    {
        printf("Error!!!\n");
    }

    // free memory
    CHECK(cudaFree(d_a));
    CHECK(cudaFree(d_b));
    CHECK(cudaFree(d_c));
    CHECK(cudaFree(d_c_share));
    CHECK(cudaFreeHost(h_a));
    CHECK(cudaFreeHost(h_b));
    CHECK(cudaFreeHost(h_c));
    CHECK(cudaFreeHost(h_cc));
    CHECK(cudaFreeHost(h_cs));
    return 0;
}

讲解部分

为了保证同样的对比，在基础版优化时申请的Shared Memory大小和形状为[BLOCK_SIZE][BLOCK_SIZE]，而进一步优化时，保证申请的Shared Memory大小不变，仅改变其形状，所以对应于矩阵M 的Shared Memory的形状为[BLOCK_SIZE/2][BLOCK_SIZE2]，矩阵N 的Shared Memory的形状为[BLOCK_SIZE2][BLOCK_SIZE/2]。例如，在上一篇博客中将shared memory统一设定为44，在本篇中则分别设定为28和8*2。

__shared__ int tile_a[BLOCK_SIZE/2][BLOCK_SIZE*2];
__shared__ int tile_b[BLOCK_SIZE*2][BLOCK_SIZE/2];

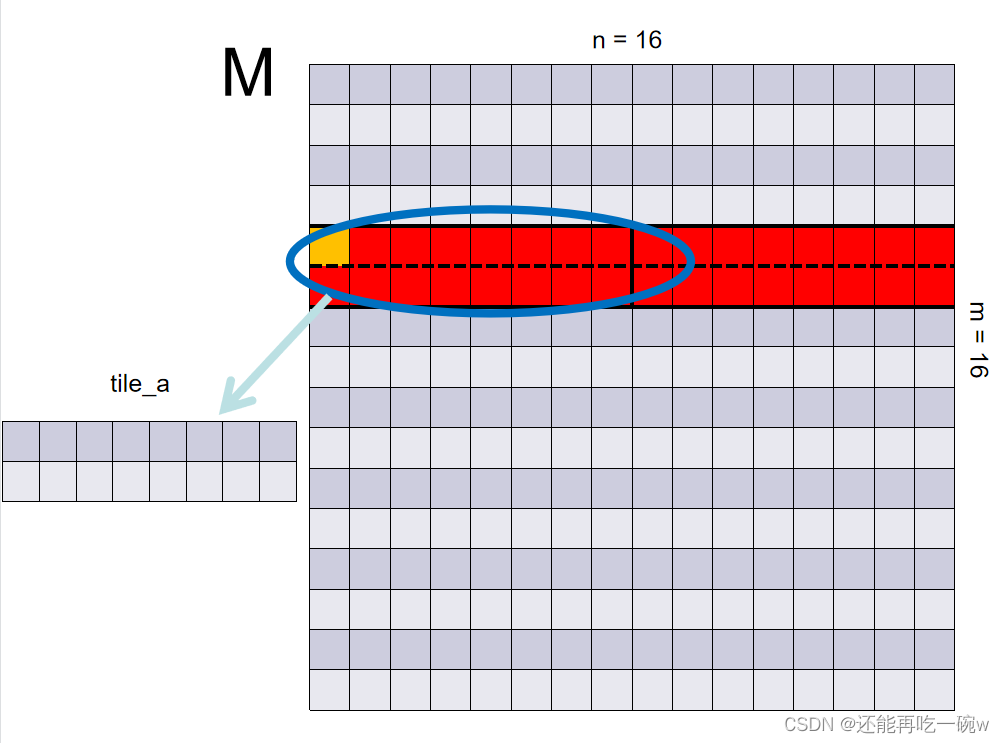
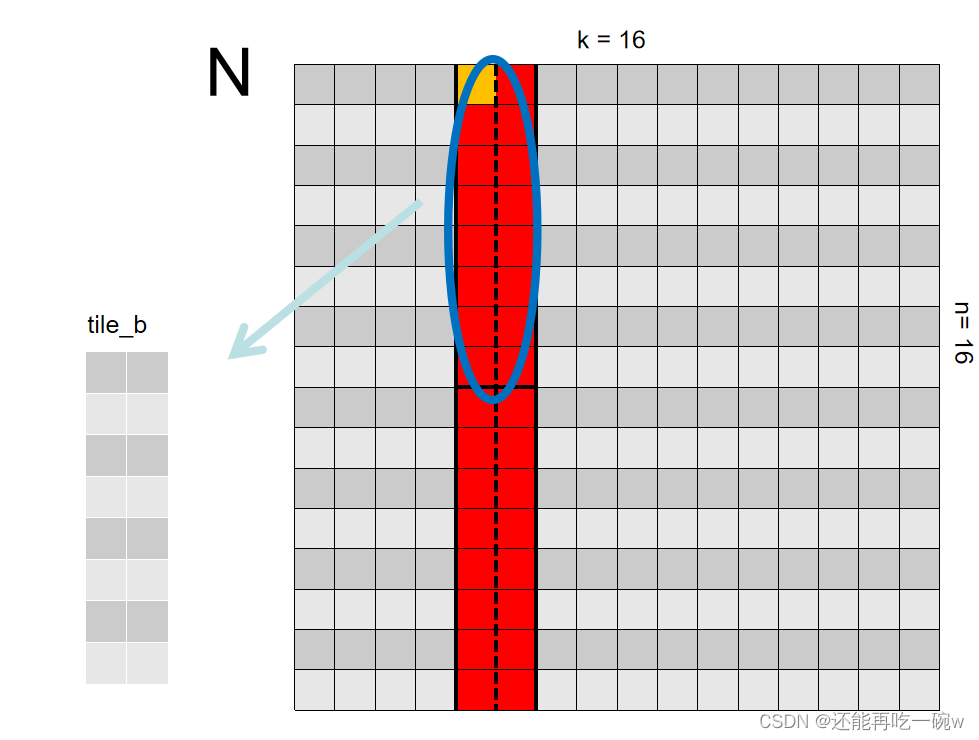
在这里插入图片描述

由于每个block对应其每块矩阵元素的求解，而将申请的shared memory尺寸改变，所得到的block尺寸也将发生改变，因此，block尺寸也变为[BLOCK_SIZE/2][BLOCK_SIZE/2]，为了保证线程数与所求矩阵C元素一一对应，因此还需要改变grid的大小。

unsigned int grid_rows1 = (m + BLOCK_SIZE - 1) / (BLOCK_SIZE / 2);
unsigned int grid_cols1 = (k + BLOCK_SIZE - 1) / (BLOCK_SIZE / 2);
dim3 dimGrid1(grid_cols1, grid_rows1);
dim3 dimBlock1(BLOCK_SIZE/2, BLOCK_SIZE/2); 
gpu_matrix_mult_test<<<dimGrid1, dimBlock1>>>(d_a, d_b, d_c, m, n, k);

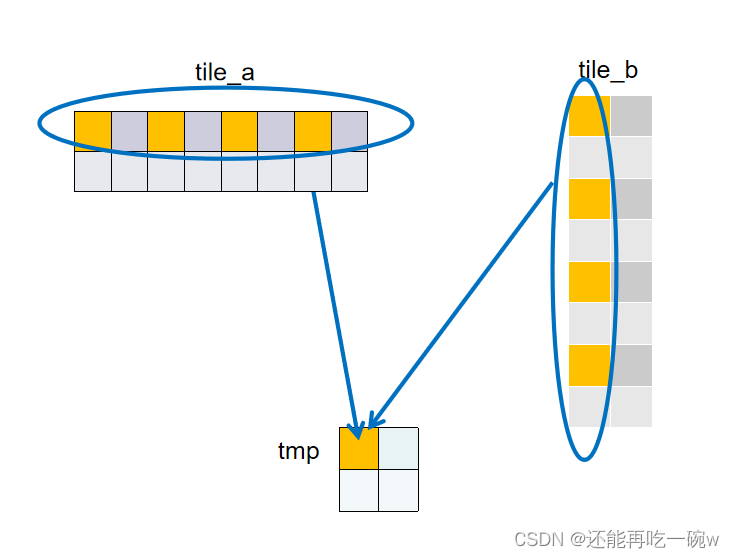
在这里插入图片描述

因为block的大小改变，因此在核函数中，无法一一对应为shared memory提取到对应矩阵的值，如上图所示，block大小为22，shared memory大小为8.2和28时，同一时间每个block需要为4个shared memory地址赋值。

idx1 = row * n + sub * BLOCK_SIZE*2 + threadIdx.x;
idx2 = row * n + sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.x;
idx3 = row * n + sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.x;
idx4 = row * n + sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.x;
        
tile_a[threadIdx.y][threadIdx.x] = row < m &&(sub * BLOCK_SIZE*2 + threadIdx.x)<n?a[idx1]:0;
tile_a[threadIdx.y][threadIdx.x + BLOCK_SIZE/2] = row < m &&(sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.x)<n?a[idx2]:0;
tile_a[threadIdx.y][threadIdx.x + BLOCK_SIZE] = row < m &&(sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.x)<n?a[idx3]:0;
tile_a[threadIdx.y][threadIdx.x + BLOCK_SIZE*3/2] = row < m &&(sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.x)<n?a[idx4]:0;
        
idx1 = (sub * BLOCK_SIZE*2 + threadIdx.y) * k + col;
idx2 = (sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.y) * k + col;
idx3 = (sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.y) * k + col;
idx4 = (sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.y) * k + col;
        
tile_b[threadIdx.y][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + threadIdx.y)<n? b[idx1]:0;
tile_b[threadIdx.y + BLOCK_SIZE/2][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + BLOCK_SIZE/2 + threadIdx.y)<n? b[idx2]:0;
tile_b[threadIdx.y + BLOCK_SIZE][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + BLOCK_SIZE + threadIdx.y)<n? b[idx3]:0;
tile_b[threadIdx.y + BLOCK_SIZE*3/2][threadIdx.x] = col<k && (sub * BLOCK_SIZE*2 + BLOCK_SIZE*3/2 + threadIdx.y)<n? b[idx4]:0;