提升方法_统计学习方法_学习笔记

最新推荐文章于 2022-07-06 17:30:40 发布

OliverLee456

最新推荐文章于 2022-07-06 17:30:40 发布

阅读量338

点赞数 1

分类专栏：机器学习笔记

本文链接：https://blog.csdn.net/OliverLee456/article/details/86572549

版权

机器学习笔记专栏收录该内容

14 篇文章 3 订阅

订阅专栏

前言

统计学习方法一书中的第7章为支持向量机的内容，由于在之前CS229笔记中已经阐述过该内容，因此不再赘述。但是由于支持向量机的内容比较多而且耐人琢磨，因此在后面可能会考虑将其中的内容（例如对偶问题、SMO等）单独拆开并深入学习从而加深理解。

这一章笔记主要讨论提升方法（boosting）的思想，并重点阐述AdaBoost算法。书中最后一节关于提升树的内容不计入该笔记之中，之后应该会单独一章笔记来谈谈对于随机森林的理解。

1 提升方法思想

提升方法（boosting）是一种常用的统计学习方法，应用广泛而且十分有效。

为了理解提升方法，首先引入强可学习（strongly learnable）与弱可学习（weakly learnable）的概念：在概率近似正确（probably approximately corect，PAC）学习的框架中，一个概念，如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的；若正确率仅比随机猜测稍好，则其为弱可学习的。有趣的是，之后Schapire证明，在PAC框架中，强可学习和弱可学习是等价的，即一个概念是强可学习的充分必要条件是这个概念同时也是弱可学习的。

需要明白的是，找到一个强可学习的算法难，但是找到一个弱可学习的算法简单。既然强可学习和弱可学习是等价的，那么我们便可以找到一个弱可学习的算法，将其“提升”为强可学习的算法，这就是提升方法的来历了。关于提升方法的研究有许多，其中最具代表性的是AdaBoost算法（AdaBoost Algorithm，适应性提升算法）。

因此，提升方法的出发点有二：一是将弱可学习算法“提升”为强可学习算法；二是认为多个算法的得到的结果比单一算法好。

具体地，对于分类问题而言，解决第一点的方式为组合各个弱分类器从而构造一个强分类器；解决第二点的方式为采用投票规则，即结果占比例最大的分类结果为最终的分类结果。

以下内容以解决二分类问题的AdaBoost算法为例进行阐述。

2 AdaBoost算法

AdaBoost算法是1995年由Freund和Schapire提出的。为了方便叙述，以下讨论的解决问题都为二分类问题。

AdaBoost算法得到的强分类器是一系列弱分类器的线性组合。每个弱分类器都是同一套训练数据集训练得到的结果，但是不同之处在于，每个训练样本是具有“权重”的概念，在每个弱分类器的学习过程中训练样本的权重不一样，具体而言，前一个弱分类器分类错误的样本在当前弱分类器学习过程中所占的权重会增大。通过调整训练样本训练权重的方式，从而能够使每个弱分类器考虑的样本具备一些差异，并且使上一次分类错误的样本在当前的弱分类器中得到更多的关注，以达到强化训练效果的目的。

对于Adaboost而言，最终求解得到的强分类器 $G(x)$ 为M个基本分类器（弱分类器） $G_{m}(x)$ 的线性组合。

M个基本分类器（弱分类器） $G_{m}(x)$ 的线性组合 $f(x)$ 如下所示：

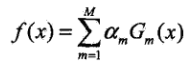
根据投票规则，得到最终的强分类器 $G(x)$ 如下所示：

因此，需要求解的是每个基本分类器 $G_{m}(x)$ 以及它们相应的系数 $a_{m}$ 。

接下来看看AdaBoost是如何“提升”的。

假设给定一个二分类训练数据集：

训练的分类标记如下。正样本类别为1，负样本为-1。

AdaBoost算法步骤如下：

（1）初始化训练数据的权重分布：

其中 $D_{1}$ 代表第一个弱分类器的采用的训练样本的权重。在第一次分类中，每个样本所占的权重一样且和为1。 $w_{ij}$ 代表第i个弱分类器的第j个训练样本的权重。

（2）计算每个基本分类器及其系数。具体地，对m=1,2...M：

（2.1）使用具有权重分布 $D_{m}$ 的训练数据集学习，得到基本分类器：

基本分类器需事先指定，如采用决策树等等。

（2.2）计算 $G_{m}(x)$ 在训练数据集上的分类误差率，同样 I 为指示函数：

$w_{mi}$ 代表在第m个基本分类器训练过程中的第i个训练样本的权重。

这里，计算分类误差率同时也可以写：

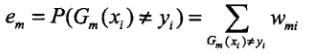
即 $e_{m}$ 的值为分类错误的样本的权重之和，且 $e_{m}$ 非负。

（2.3）计算 $G_{m}(x)$ 的系数 $a_{m}$ ：

其中对数为自然对数。为什么要这样计算，将在第3小节的AdaBoost解释中进行阐述。

观察上式可发现， $a_{m}$ 可正可负。当 $e_{m}\geq \frac{1}{2}$ 时， $a_{m}\leq 0$ ；当 $e_{m}< \frac{1}{2}$ 时， $a_{m}> 0$ 。为了方便叙述，当 $e_{m}\geq \frac{1}{2}$ 时，我将其称为差基本分类器；当 $e_{m}< \frac{1}{2}$ 时我将其称为好基本分类器。

（2.4）更新训练数据集的权重分布，即计算下一个基本分类器使用的权重分布：

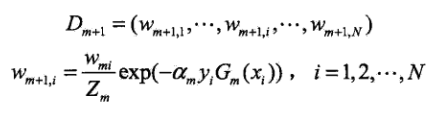
这里 $Z_{m}$ 为归一化分母，使下一次的采用权重的总和为1。即：

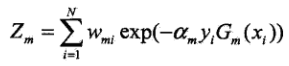
观察得到，权重的变化与系数 $a_{m}$ 以及第 i 个样本是否正确分类有关（ $y_{i}G_{m}(x_{i})$ ）。

我想在这里稍微深入一下，结合（2.3），可分以下4种情况进行讨论进行讨论：

（2.4.i）差基本分类器（ $a_{m}\leq 0$ ），分类错误（ $y_{i}G_{m}(x_{i})=-1$ ）：

此时若分类器越差，即 $e_{m}$ 趋近于1， $a_{m}$ 趋近于负无穷， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于0，即更新之后所占权重越小。

此时若分类器越好，即 $e_{m}$ 趋近于 $\frac{1}{2}$ ， $a_{m}$ 趋近于0， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于1，即更新之后权重变化不大。

（2.4.ii）差基本分类器（ $a_{m}\leq 0$ ），分类正确（ $y_{i}G_{m}(x_{i})=1$ ）：

此时若分类器越差，即 $e_{m}$ 趋近于1， $a_{m}$ 趋近于负无穷， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于正无穷，即更新之后所占权重越大。

此时若分类器越好，即 $e_{m}$ 趋近于 $\frac{1}{2}$ ， $a_{m}$ 趋近于0， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于1，即更新之后权重变化不大。

（2.4.iii）好基本分类器（ $a_{m}> 0$ ），分类错误（ $y_{i}G_{m}(x_{i})=-1$ ）：

此时若分类器越差，即 $e_{m}$ 趋近于 $\frac{1}{2}$ ， $a_{m}$ 趋近于0， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于1，即更新之后权重变化不大。

此时若分类器越好，即 $e_{m}$ 趋近于0， $a_{m}$ 趋近于正无穷， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于正无穷，即更新之后权重越大。

（2.4.iV）好基本分类器（ $a_{m}> 0$ ），分类正确（ $y_{i}G_{m}(x_{i})=1$ ）：

此时若分类器越差，即 $e_{m}$ 趋近于 $\frac{1}{2}$ ， $a_{m}$ 趋近于0， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于1，即更新之后权重变化不大。

此时若分类器越好，即 $e_{m}$ 趋近于0， $a_{m}$ 趋近于正无穷， $exp(-a_{m}y_{i}G_{m}(x_{i}))$ 趋近于负无穷，即更新之后权重越小。

虽然我区分了4种情况，但是一般而言， $a_{m}$ 非负是基本的要求。因为基本分类器选取的是弱分类器，而不是错误的分类器。

由此，可以发现AdaBoost设计的权重更新思想：强化好的基本学习器分类错误的惩罚，弱化了差的学习器分类正确的惩罚。

除此之外，还可将（2.1）的更新方式进行如下改写：

由此也可以得到，误分类的样本的权重被扩大了：

即被分类错误的样本在下一个基本分类器学习过程中将占更多的权重。

在每个基本分类器的学习过程中，不改变训练数据，通过改变训练数据权重的方式使得每个基本分类器能够有区别的对待同一份训练数据，是AdaBoost的一个特点。

（3）通过上一步，得到M个基本分类器和他们的系数，以此构建基本分类器的线性组合：

从而在此基础上，根据投票规则，得到最终的强分类器：

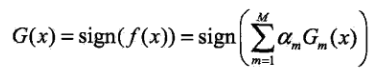
系数 $a_{m}$ 代表的每个基本分类器的重要程度。 $f(x)$ 的正负符号代表最后的结果。 $f(x)$ 的绝对值代表着分类的确信程度。因此 $G(x)$ 取值范围为{1,-1}。 $G(x)$ 反应的是最终的结果应该由M个基本分类器线性组合而成。

3 AdaBoost算法的误差分析

AdaBoost的训练误差界，即AdaBoost算法最终分类器的训练误差界为：

前一个不等式较好证明：因为当 $G(x_{i}) \neq y_{i}$ 时， $y_{i}f(x_{i})<0$ ，因为 $exp(y_{i}f(x_{i}))\geq 0$ ，因此直接简单的放缩，便可以得到第一个不等式。

第二个不等式并没有看明白，暂且贴在这里：

推导过程需要用到一个变形：

推导过程如下：

观察误差界的推导可以发现，误差的上界可在每一个基本分类器权重确定后通过其归一化因子 $Z_{m}$ 得到。因此在每一轮都使训练的误差最小，那么总的训练误差就是最小的。因此这也是为什么AdaBoost算法收敛的原因。

下面来看看二分类问题的训练误差界：

其中：

证明过程向比较而言清晰一些，先证明左边的等式；

第一行直接展开 $Z_{m}$ 表示式。

第二行将其分为正确分类与错误分类两项。

第二行到第三行，通过加上 $\sum _{y_{i}\neq G_{m}(x_{i})}w_{mi}e^{-a_{m}}$ ，并减去 $\sum _{y_{i}\neq G_{m}(x_{i})}w_{mi}e^{-a_{m}}$ ，进行合并化解得到。

第三行带入 $a_{m}$ 表达式即可得到，即：

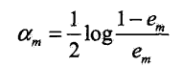
至于右边不等式，可由 $e^{x}$ 和 $\sqrt{1-x}$ 在点x=0的泰勒展开式推出。我在这里就不深究了，有兴趣可以去证明一下。

由AdaBoost二分类误差界，可以得到一个推论，若存在一个下界 $\gamma >0$ ，使得对所有m有 $\gamma_{m} >\gamma$ ，则

我们并需要知道下界 $\gamma$ 的值准确的是多少，此推论的目的在于让我们知道，AdaBoost的误差是以指数级下降的，该算法收敛得很快。与一些早期的提升方法不同，AdaBoost（Adaptive Boost）具有适应性，即它能适应弱分类器各自的训练误差率，这也是它名称的由来。

4 AdaBoost算法的进一步解释

AdaBoost算法的另一种解释为，认为AdaBoost是模型为加法模型，损失函数为指数函数，学习算法为前向分布算法时的二分类算法。别被上面一句话唬住了，其实具体看看，就明白了。

（1）加法模型（additive model）：

加法模型结果 $f(x)$ 由M个基函数 $b(x;\gamma _{m})$ 组成。其中 $\gamma _{m}$ 为基函数参数。 $\beta _{m}$ 为基函数的系数。那么AdaBoost的最终强分类器便是一个加法模型。

（2）指数损失函数：

给定训练数据和损失函数 $L(y,f(x))$ 的情况下，加法模型的指数损失函数形式如下：

（4.1）

（3）前向分步算法（forward stagewise algorithm）：

前向分步算法可用来求解优化问题（4.1）。优化思路即为，在每一步的学习过程中，不关心其他基函数，一步只求解一个基函数的系数和其参数使其最优，从而使整体最优。有点像坐标上升算法。

其实以上就是对于AdaBoost算法的步骤给了一些明确的定义。

接下来，具体推导一下，即当模型为加法模型，基函数为基本分类器，损失函数为指数函数时，利用前向分步算法推导得到的分类器的形式等价于AdaBoost得到的分类器结果。

首先，定义损失函数：

现在由于基本分类器已经确定，要求解的便是基本分类器的系数 $a_{m}$ 。

假设经过m-1轮训练得到：

在m轮学习后得到：

目标是使得到的 $a_{m}$ ， $G_{m}(x)$ 使 $f_{m}(x)$ 的指数损失最小，即：

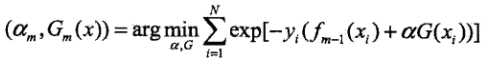
可将上式改写为：

（4.2）

其中：

因为其与a和G都无关，因此在优化公式（4.2）时，将其作为一个常数项进行处理。但是应该注意的是，其虽然与当前基本分类器无关，但是与之前的基本分类有关。

为了优化公式（4.2），我们需要将a和G拆开来讨论。

首先对于任意的 $a>0$ ，最小的G可由下式得到（经验误差最小化）：

接下来看a。可将（4.2）进行如下改写：

在上面二者的基础上，将求得的最小的 $G_{m}^{*}(x)$ 带入，对a求导并使导数为0，即可得到a的结果如下：

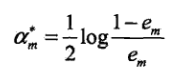
系数的结果与AdaBoost一致。其中 $e_{m}$ 代表分类误差率：

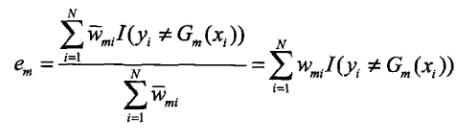
再看看参数的更新情况：

与AdaBoost只差一个分母，即归一化因子 $Z_{m}$ 。

因此也可以把AdaBoost看作是一种改进：即当学习模型为加法模型，损失函数为指数函数，学习算法为前向分步算法时的一个特例。

5 小结

当AdaBoost算法中的基本分类器选用决策树时即为书中所提到的提升树，该部分内容不再这里叙述，以后结合随机森林再进行讨论。

应该明白的是，提升方法的目的在于使弱学习器“提升”为强学习器，因为寻找到若干个弱学习器的难度远远小于构造一个强学习器的难度。

AdaBoost便是提升方法中非常经典的算法。其思路在于通过将一些弱学习器通过线性组合的形式合并为一个强学习器。其一个重要的核心在于每个基本分类器虽然在同一个训练数据集上进行训练，但是训练的样本的权重却不一样，也就是说上一个基本分类器分类错误的样本会在当前基本分类器中占有更多的权重。而第3节的AdaBoost算法的误差分析表明，AdaBoost的每次迭代可以减少它在训练数据集上的分类误差率，因为每次迭代都使经验误差最小，这说明了它作为提升方法的有效性。

OliverLee456

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
提升方法_统计学习方法_学习笔记

前言统计学习方法一书中的第7章为支持向量机的内容，由于在之前CS229笔记中已经阐述过该内容，因此不再赘述。但是由于支持向量机的内容比较多而且耐人琢磨，因此在后面可能会考虑将其中的内容（例如对偶问题、SMO等）单独拆开并深入学习从而加深理解。这一章笔记主要讨论提升方法（boosting）的思想，并重点阐述AdaBoost算法。书中最后一节关于提升树的内容不计入该笔记之中，之后应该会单独一章笔...
复制链接

扫一扫