在线性代数中我们都知道对于一个mxn的矩阵A,假设其中的特征值为k,其对应的特征向量为a。那么有:
上面的a为特征向量,k为对应的特征值。假设由|E-kA| = 0我们一共解的有i个特征值分别为:
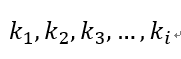
对A进行特征值分解可以得到:
这里A是作为方阵的求法。更一般的我们吧这种由特征值分解求A的做法推广到mXn矩阵:
上面的式子中m>n或者n<m或者m=n都可能存在,因此如果m!=n时候,我们得到的奇异值也就是对应K矩阵的ki,那么我们可以把整个矩阵相对应的重新排列,从上到下,从左到右按奇异值的从大到小依次排列下来得到新的矩阵K,当然对应的其他的矩阵也做对应的变换,这样的矩阵可能出现到某一行或者某一列之后全都是0行或者0列。在机器学习中我们通过实验取前面从k1,k2,k3,...,kp个特征值,其他的舍弃,也就是置为0.通过上面的矩阵变换去近似求解A。
这就是机器学习SVD算法的由来。所以学好编程,学好ML,学好DL,学好CV,首先要学好数学。
这就是m和n不相等时候,K矩阵,这里S就是K。
这里更为好奇的是对于一般的mxn的矩阵A,该如何进行SVD分解呢?
我们尝试看看A和A的转置的乘积问题:
从这里看出来,中间的矩阵E对角线上的元素其实是A和A的转置的乘积的特征值,用它们来表征A的奇异值。
这里可以得到最终的上面的近似解,可以简化计算量,同时把主要的特征取到,也就是对应的前面P大的奇异值。这里的r越接近n近似解越逼近A。
import numpy as np
import os
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib as mpl
from pprint import pprint
# 通过特征值和特征向量求解矩阵的近似解函数
def restore1(sigma, u, v, k):
# 获取矩阵U的长度,上面的sigma u v k分别为特征值,左特征向量,右特征向量,截取的SVD前K个奇异值
m = len(u)
# 获取V的长度
n = len(v[0])
# 向量(矩阵)保存着恢复过来的像素
a = np.zeros((m,n))
for k in range(k):
uk = u[:, k].reshape(m, 1)
vk = v[k].reshape(1, n)
a += sigma[k] * np.dot(uk, vk)
# 对于矩阵变换得到的矩阵a,把元素值小于0的置0,大于255的置255
a[a < 0] = 0
a[a > 255] = 255
# a = a.clip(0, 255)
return np.rint(a).astype('uint8')
def restore2(sigma, u, v, k):
m = len(u)
n = len(v[0])
a = np.zeros((m, n))
for k in range(k + 1):
for i in range(M):
a[i] += sigma[k] * u[i][k] * v[k]
a = a.clip(0, 255)
return np.rint(a).astype('uint8')
if __name__ == "__main__":
# 读取图像
A = Image.open("test2.png", 'r')
# 创建保存中间结果的目录
output_path = r"./getPic"
if not os.path.exists(output_path):
os.mkdir(output_path)
# 转换为numpy的向量
a = np.array(A)
print("像素:\n", a)
# 要进行近似求解前k个奇异值
k = 100
u_r, sigma_r, v_r = np.linalg.svd(a[:, :, 0])
print("r :\n", a[:, :, 0])
u_g, sigma_g, v_g = np.linalg.svd(a[:, :, 1])
print("g :\n", a[:, :, 1])
u_b, sigma_b, v_b = np.linalg.svd(a[:, :, 2])
print("b :\n", a[:, :, 2])
plt.figure(figsize=(10, 10), facecolor='w')
# 进行恢复
for k in range(1, k+1):
print(k)
new_R = restore1(sigma_r, u_r, v_r, k)
new_G = restore1(sigma_g, u_g, v_g, k)
new_B = restore1(sigma_b, u_b, v_b, k)
new_A = np.stack((new_R, new_G, new_B), axis=2)
Image.fromarray(new_A).save("%s//svd_lena__%d.png" %(output_path, k))
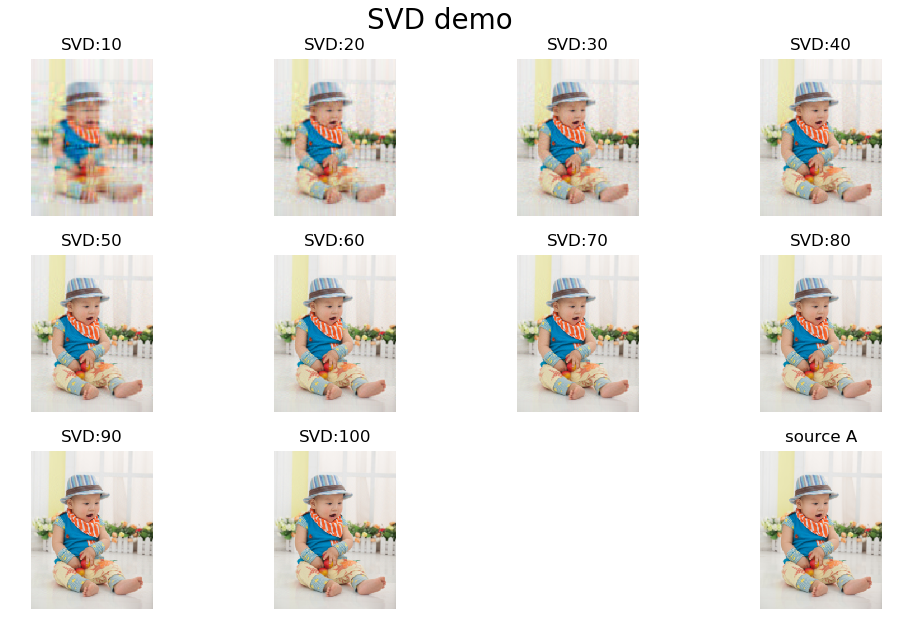
# 部分显示过程SVD恢复的图像
if k % 10 == 0:
plt.subplot(3, 4, int(k/10))
plt.imshow(new_A)
plt.axis('off')
plt.title("SVD:%d" % k)
plt.subplot(3,4,12)
plt.imshow(A)
plt.title("source A")
plt.axis('off')
# 对显示的figure进行调整
plt.suptitle("SVD demo", fontsize=20)
plt.tight_layout(2)
plt.subplots_adjust(top=0.9)
plt.show()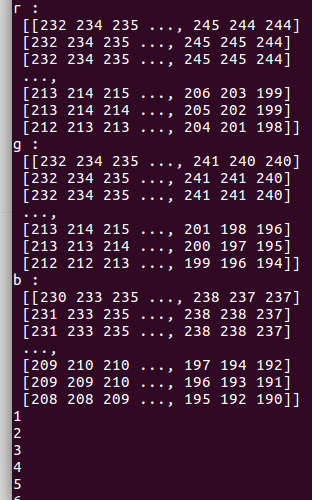













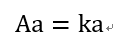
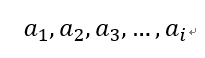
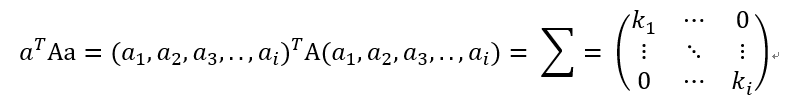

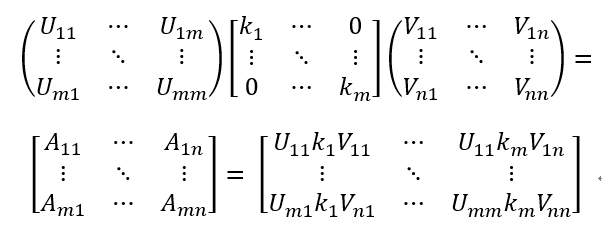

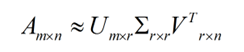
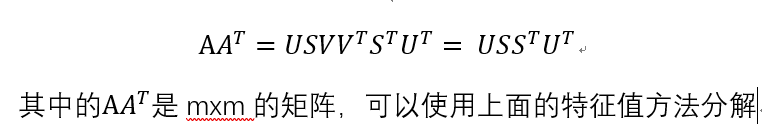















 2732
2732

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








