林轩田机器学习技法（Machine Learning Techniques）笔记（一）

终于到机器学习技法了，接下来还是尽量保持每章完结就立刻更吧。。基石没有保持写完就更，现在回头不知道自己在写啥，看笔记感觉写得一塌糊涂，感觉翻车了。慢慢改进吧。
听说技法挺难的，贴一下大神博客来加持一发：
红色石头：感觉总结得非常不错！！

林轩田机器学习技法（Machine Learning Techniques）笔记（二）
林轩田机器学习技法（Machine Learning Techniques）笔记（三）

1. Linear SVM

P1 1.1
介绍了本课程之后围绕三个特征转换(feature transforms)的【技法】来讲
1.如何运用特征转换和控制特征转换的复杂度：用SVM（Support Vector Machine，听说挺难的）
2.如何找到有预测性质的特征，并且混合起来让模型表现更好：AdaBoost（逐步增强法）
3.如何找到和学习隐藏的特征，让机器表现更好：Deep Learning（深度学习！！！）

---

P2 1.2

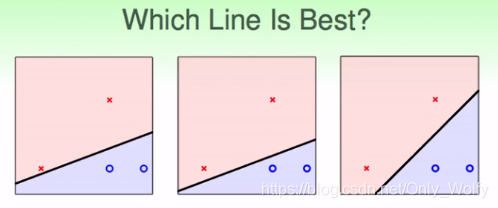
在PLA中，我们对于一组数据，其实可以有不同的划分。上面三幅图都是"正确的"：保证了所有点都划分对了，而且根据VC bound，Eout都是一样的

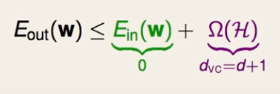
但是根据人脑来说，肯定是最右边那幅图的划分更好。
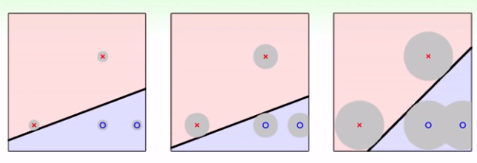
为什么呢？因为数据会有一些噪音或者测量误差，使得实际情况下并不是一定在ooxx上，可能会分布在灰色区域，而且也都是合理的。如果是在左图，靠近分界线上的x，如果有一些震荡，就会比较容易跑去o的范围内，导致出错。因此，为了提高的容错率（容忍误差能力）（传说中的鲁棒性？），要调出比较"强壮的"线，显然，最强壮的线是保证所有东西都分对了的情况下，离最近的点距离最远的线。


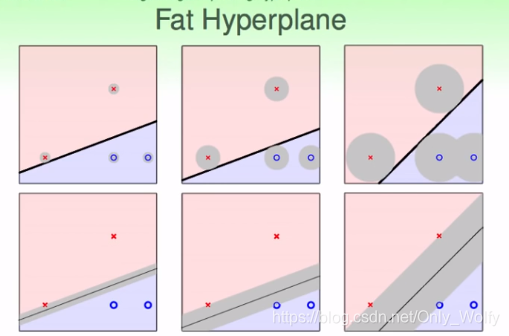
当然，也可转化为线“胖”不“胖”，越胖的线越强壮。学术上称“胖”为margin。下面则是用公式表达出margin最大化的w：“最强壮的线是保证所有东西都分对了的情况下，离最近的点距离最远的线”

---

P3 1.3

开始求distance(xn,w)，之前是在w1~wd中加入一个w0的，但是因为这个w0和其他w操作不一样，就直接单独跳出来，即为b，因此就有：

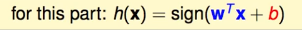
（这里的w0(b)应该是偏置项吧，对于为什么有偏置项，详细还得看看西瓜书）

接下来要找到distance(x,b,w)，x’ 和 x’’ 是平面上的点，x是数据点（不一定在超平面上），根据wTx’ + b = 0，就有wTx’ = -b，同理：wTx’’ = -b

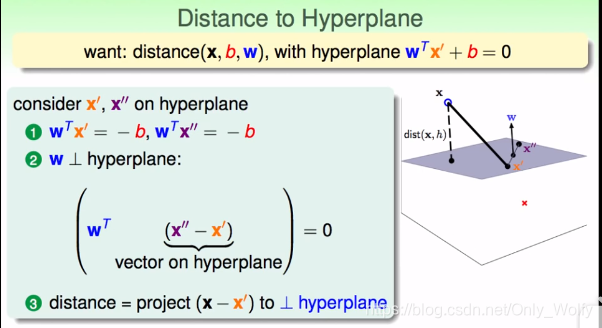
这里有个特别地方，就是证明了w是这个超平面的法向量。（关于超平面，看了一下别人的文章，不过他好像没有讲为啥w是法向量。。）
知道了法向量，如果平面上有一点x’，x和x’的距离distance其实就是向量xx’在w上的投影，所以就是：

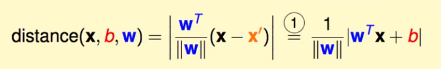
因为这是个Hard-Margin的SVM，所以这条线对于所有的点，都会分对，所以就有：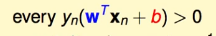
且yn=±1，所以可以脱去绝对值：

接下来为了方便求解：
定义：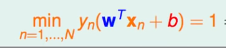
那么就有：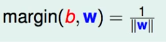
对于为什么为1，其实任意常数都可以，这里看弹幕说涉及了函数间隔和几何间隔的知识？？。看红色石头说对w和b同时缩放，得到的平面还是一样的，所以可以控制$y_n(w{1}^T{x}_n+b1)=1$（哦 O o ？？）
此时，因为要求最大的margin（让线更宽），所以要让w更大，并满足$mi{n}_{(}n=1...N)y_n(w{1}^T{x}_n+b1)=1$

但是还是比较难解，于是我们把条件放松，让$y_n(w^T{x}_n+b1)>=1$，并证明放松后，最佳解还是h会满足$y_n(w^T{x}_n+b1)=1$
假设找到有组最佳解(b1,w1)使得$y_n(w{1}^T{x}_n+b1)>1.126$，那么我们还可以找到一组更优的解($\frac{b1}{1.126}$，$\frac{w1}{1.126}$)，根据$margin=\frac{1}{||w||}$，w/1.126后变小了，从而让margin更大。因此，之前的最优解(b1,w1)并不是最优的，存在矛盾。所以只要有组解使得$y_n(w^T{x}_n+b1)>1$，我们就能够找到更优的解使得$y_n(w^T{x}_n+b1)=1$，因此，我们得知最优解会使$y_n(w^T{x}_n+b1)=1$。

最后，之前都是求min，为了统一一下，把$\frac{1}{||w||}$取倒数。从求$max\frac{1}{||w||}$变为求 $min||w||$。因为||w||有根号，所以除掉根号，变为w的平方，用矩阵表示就是wTw，最后再加上$\frac{1}{2}$（感觉是为了求导而加的？？）。最后变成：

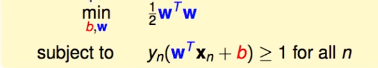
最后的funtime，注意式子x1x2可以分别对应y=kx+b中的x和y。然后根据$d=\frac{|Ax1+Bx2+C|}{\sqrt{(A^2+B^2)}}$，化简$x1+x2=1$为$1\ast x1+1\ast x2-1=0$，则$A=1,B=1,C=-1$，代入x1的x1，x2（其实就是x1的x和y），就是下面这里：

---

P4 1.4

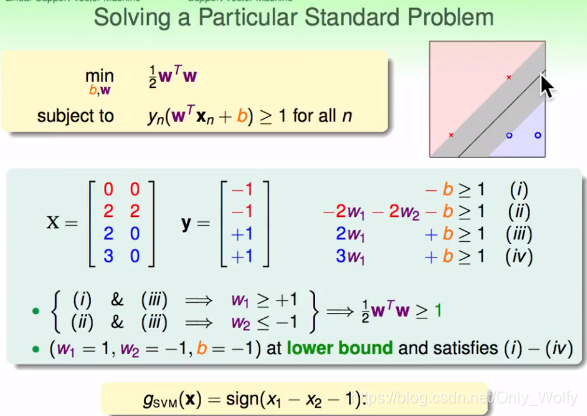
以这组（X,Y）为例子，可以得出(i)~(iv)，那么可以确定出w1>=1,w2<=-1，所以w1^2 + w2^2 >=2，所以有$\frac{1}{2}{w}^{T}w>=1$，给w1，w2和b赋合适的值，则得出了g_svm = sign ( x1 - x2 - 1 ) 。
那么，如何处理一般情况呢？解决的这个问题：
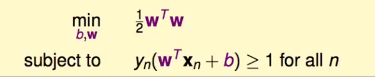它有两个特点：

而quadratic programming（二次规划 / 凸优化 / 是个QP问题）已经有一个已知的解决方法了，接下来只有代入就好了：

最后，对于不是线性的问题，用之前那个z空间就可以了

---

P5 1.5
SVM和之前那个正则化regularization（z空间啥的）的区别喊联系：

可以看出他们两个的目标差不多是相反的，所以SVM也是一种regularization，不过让Ein=0而已。

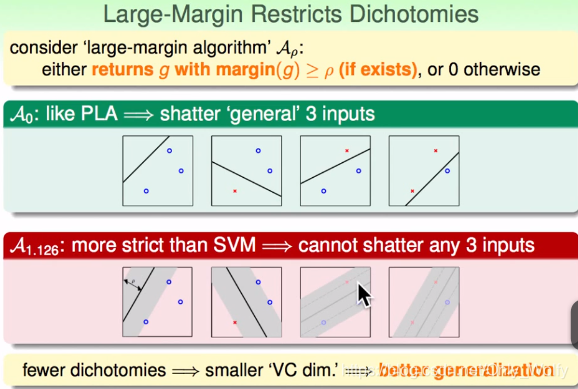
当margin设为0的时候($A_0$)，跟PLA一样。宽度为A_1.126时候，如果不符合规则就不选的话，会比$A_0$的种类少，因此情形少了->（假的）VC dimension少了->better generalization。

对于这个球 $\rho =0$的时候可以shatter 3 个点，所以 d_vc = 3，如果 $\rho =\frac{\sqrt{3}}{2}$的话，这个圆半径为$\sqrt{3}$，因为有三个点，最多一对在对面，还有另一个点不能被shatter，所以此时d_vc < 3 。因此有：

下节课会介绍把large-margin hyperplanes和特征转换结合起来的non-linear SVM：