字符串查找---用16幅图从暴力一步步优化到KMP

题目

给定一个字符串 S ，以及一个模式串 P ，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式
第一行输入整数 N ，表示字符串 P 的长度。

第二行输入字符串 P 。

第三行输入整数 M ，表示字符串 S 的长度。

第四行输入字符串 S 。

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围
1≤N≤10⁵

1≤M≤10⁶
输入样例：
3
aba
5
ababa
输出样例：
0 2

先来解释一下字符串查找的含义。

字符串查找：有一个长的字符串S，和一个短的字符串P，如果短的字符串P在长的字符串S中出现过，输出第一次出现的位置，否则输出 -1。

例如：长的字符串 S = “ababababfab” ，短的字符串 P = “ababf”，可以看出 P 在 S 中第一次出现位置是在S[4] 到S[8]，所以输出4。

例如：长的字符串 S = “abababfab” ，短的字符串 P = “ababg”，可以看出 P 在 S 中没有出现过，输出 -1。

最容易想到的做法是：暴力求解。

依次比较以长字符串各个字母为开头的子串是否与短字符串匹配。

如果有匹配的输出起始位置，如果没有，输出 -1。

例如：以长的字符串 S = “ababababfab” ，短的字符串 P = “ababf” 为例，过程如下：

首先用S[0]开头的子串：ababa 与 P比较，不匹配。

接着用S[1]开头的子串：babab 与 P比较，不匹配。

接着用S[2]开头的子串：ababa 与 P比较，不匹配。

接着用S[3]开头的子串：babab 与 P比较，不匹配。

接着用S[4]开头的子串：ababf 与 P比较，匹配。输出4。

代码如下：

//cpp
int ViolentMatch(string& s, string& p)//s为长字符串，p为短字符串。
{
    for (int i = 0; i < m;)
    {
        int start = i, j = 0;//star 记录此次s中的开始位置
        while (i < m && j < n && s[i++] == p[j++]);//一次比较，直到不相等，注意句尾带分号
        if (j == n)//如果p串比较完了，返回开始位置
        {
            cout << start;
            return 0;
        }
        i = start + 1;//i更新到本次起始位置的下一个位置
    }
    cout << -1;
    return -1;
}

在时间上，两个循环分别是 m， n， 所以时间复杂度是O(m * n)。空间上没有开辟与字符串有关的空间，所以空间复杂度是O(1)。

怎么从暴力解法优化到KMP算法呢？

咱们来一步一步优化。还以长的字符串 S = “ababababfab” ，短的字符串 P = “ababf”为例。这里有点绕。

首先用S[0]开头的子串：“ababa” 与 P = “ababf” 比较，比较到 S[4] 与 P[4] 的时候，S[4] != P[4]。

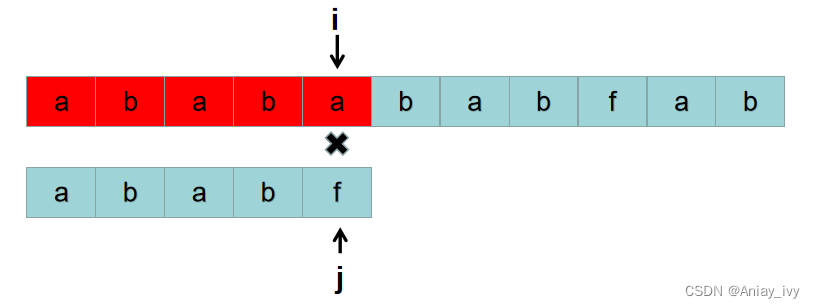
按照暴力的思路，接下来是用S[1]开头的子串： P = “babab“ 与 P = “ababf“ 比较。

这时候，如果有位无所不知的上帝，他告诉我们：S[1~3] 与 P[0~2] 不匹配，那以S[1] 为开头的字符串肯定与 P 不匹配。我们就无需进行以S[1]开头子串与 P 的比较了。

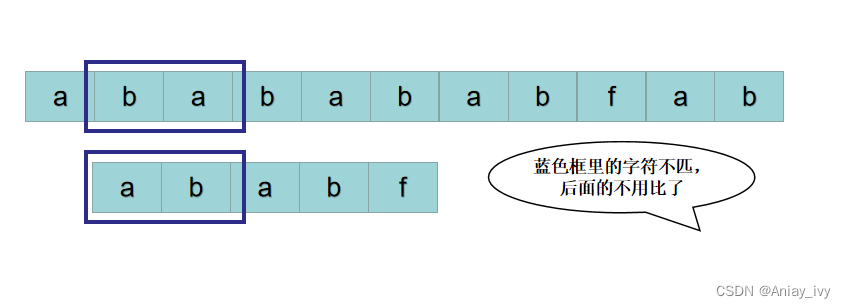
从哪里找来上帝？先假设有这么一位上帝，后面会介绍从哪里找来。

按照暴力的思路，接下来用 S[2] 开头的子串： P = “ababa“ 与 P = “ababf“ 比较。

这时候，上帝又告诉我们，S[2~3] 与 P[0~1] 匹配，那以S[2] 为开头的字符串与 P 匹配时，无需从S[1]开始，直接从S[4] 与 P[2] 开始比较即可。比较到S[6] 与 P[4] 的时候，S[6] != P[4]。

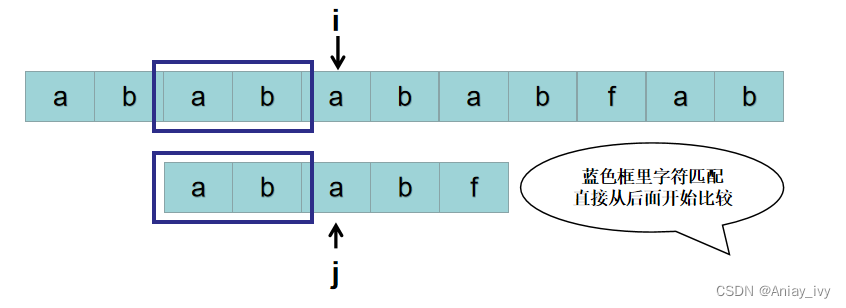
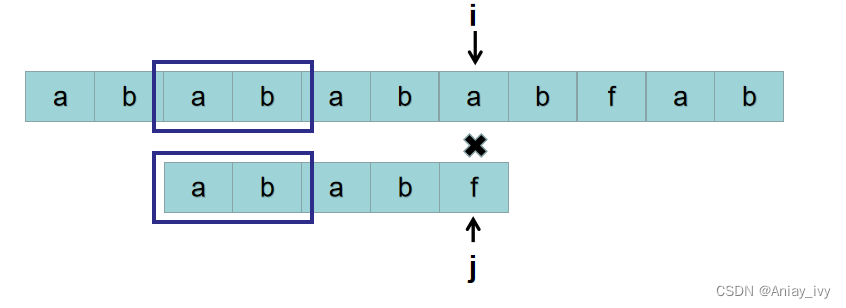
按照暴力的思路，接下来用 S[3] 开头的子串： P = “babab“ 与 P = “ababf“ 比较。

这时候，上帝又告诉我们，S[3~5] 不等于 P[0~2]，那以S[3] 为开头的字符串肯定与 P 不匹配。我们就无需进行以S[3]开头子串与 P 的比较了。

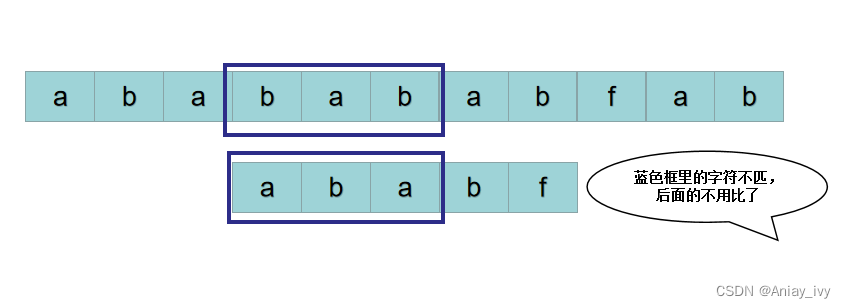
按照暴力的思路，接下来用 S[4] 开头的子串： P = “ababf“ 与 P = “ababf“ 比较。

这时候，上帝又告诉我们，S[4~5] 与 P[0~2] 相同，那以S[4] 为开头的字符串与 P 匹配时，无需从S[4]开始，直接从S[5] 与 P[3] 开始比较即可。比较到S[8] 与 P[5] 的时候，S[8] = P[5]，字符串匹配完成，返回起始位置4。

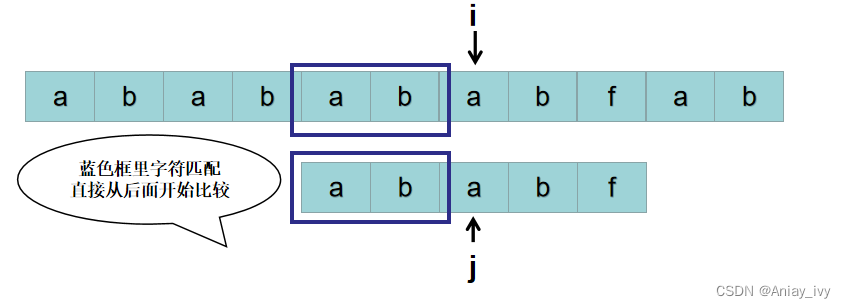
上帝的作用是: 当匹配过程中，出现了 S[i ] != P[j]，上帝会告诉我们： S[i-j+1 ~ i-1] 与 P[0 ~ j-2] 是否匹配，S[i-j+2 ~ i-1] 与 P[0 ~ j-3] 是否匹配···。也就是下图中 S 蓝色框里的子串与 P 蓝色框里的子串是否匹配，S 绿色框里的子串与 P 绿色框里的子串是否匹配，S 红色框里的子串与 P红色框里的子串是否匹配。

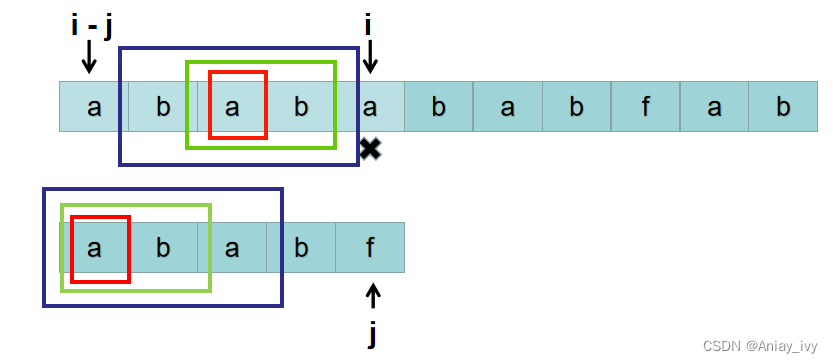
其实上帝只需要告诉我们一个值 k，k 是能满足下面性质的最大值:

1. 长字符串从 i-k 到第 i-1 的字符 S[i-k ~ i-1] 与短字符串前k个字符 P[0 ~ k-1] 相同。

就能分析出上帝之前要告诉我们的所有信息，对于大于 0 的 x:

2. 长字符串从 i-k-x 到第 i-1 的字符 S[i-k-x ~ i-1] 与短字符串前 k-x 个字符 P[0 ~ k+x-1] 不相同。
3. 长字符串从 i-k+x 到第 i-1 的字符 S[i-k+x ~ i-1] 与短字符串前 k-x 个字符 P[0 ~ k-x-1] 相同。

我们还能分析出下面信息：

1. 因为 k 是满足 P[0 ~ k-1] 与 S[i-k ~ i-1] 相同的最大值，所以 P[0 ~ k-1+x] 与 S[i-k-x ~ i-1] (x>0) 不同，因此以 S[i-k-x] 为开头的子串与 P 肯定不匹配。下次匹配，i 无需回溯到 i-k-x， 只需回溯到 i-k，j 回溯到 0。
2. 又因为 P[0 ~ k-1] 与 S[i-k ~ i-1] 相同，因此这一段无需比较。故 i 直接可以移动到回溯之前的位置，j 直接可以移动到 k 。
3. 整体来说：当遇到不匹配的字符的时候，i 不往前移动，j 移动到 k 即可。

有了上帝提供的信息，当出现字符不匹配的情况时，i 无需往后移动，j 移动到 k。时间复杂度将低为 O(n + m)。

以长的字符串 S = “ababababfab” ，短的字符串 P = “ababf” 为例：

第一次出现字符不匹配的时候为：S[4] != P[4]。保证 P[0 ~ k-1] = S[ 4-k ~3] 的 k 的最大值为 2。

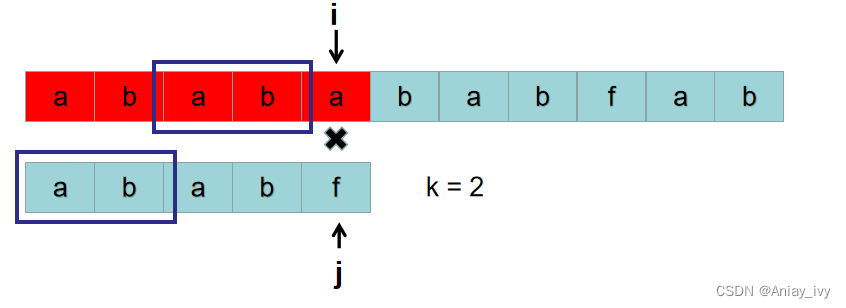
因为 k 的最大值为 2, 所以 P[0 ~ 2+1-1] != S[2-1 ~ 3]， 即 P[0 ~ 2] != S[1 ~ 3]。因此以 S[1] 为开头的子串与 P 肯定不相同，无需进行后续比较。

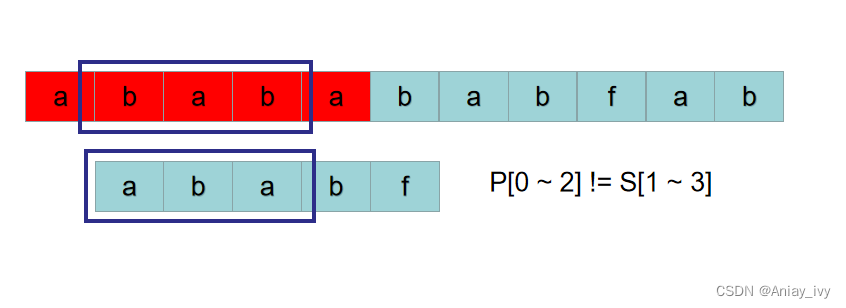
接下来判断以 S[2] 为开头的子串与 P 是否相同。又因为 P[0 ~ 1] = S[2 ~3]，所以以 S[2] 为开头的子串是否与 P 相同，只需要从 P[2] 与 S[4] 开始比较即可。i 之前的位置为 4，现在还是 4，相当于 i 没有回溯。j 之前的位置是 4 ，现在是 2，也没有回溯到 0。

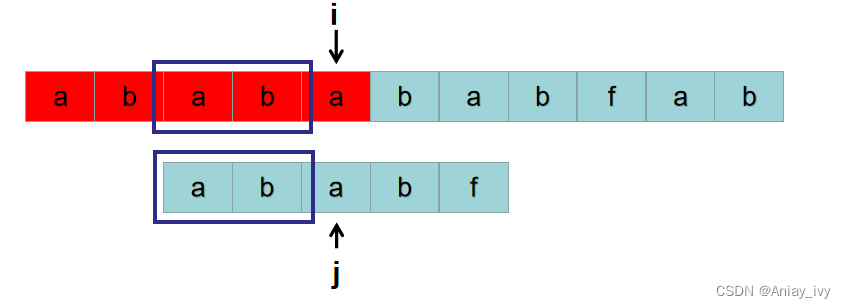
那上帝去哪找？

分析下上帝的作用：

给出一个最大的 k 值，使得短字符串 P 的前 k 个字符 P[0 ~ k-1] 与长字符串 S 的从 i-k 到第 i-1 个字符 S[i-k ~ i-1] 相同(如果k 为0，表示没有相同部分，下同)。 又因为 i 前面的字符已经匹配过了，所以 S[0 ~ i-1] 与 P[0 ~ j-1] 相同。等价于给出了一个 0 ~ j-1中的最大的 k，使得 P[0 ~ k-1] 与 P[j-k ~ j-1] 相同。这就是KMP中大名鼎鼎的最长公共前后缀长度数组:next。next[j]含义是：P[j] 前面的字符串的最长公共前后缀长度。有点绕口，看下面例子：

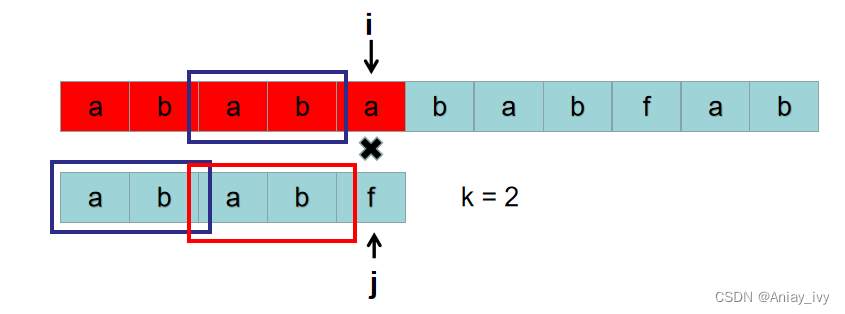
P=“ababf” 的最长公共前后缀：

1. P[0] 前面没有字符串，所以最长公共前后缀长度为 0。
2. P[1] 前面的字符串为：a，a没有前后缀(前后缀长度要小于字符串长度)。最长公共前后缀长度为 0。
3. P[2] 前面的字符串为：ab，它的前缀为：a，后缀为b。前缀不等于后缀，所以没有公共前后缀，最长公共前后缀长度为 0。
4. P[3] 前面的字符串为：aba，aba 的前缀有：a，ab， 后缀有：a，ba。因为 ab 不等于 ba，所以最长公共前后缀为 a，最长公共前后缀长度为 1。
5. P[4] 前面的字符串为：abab，abab 的前缀有：a，ab，aba，后缀有：a，ab, bab。最长公共前后缀为 ab，长度为 2。

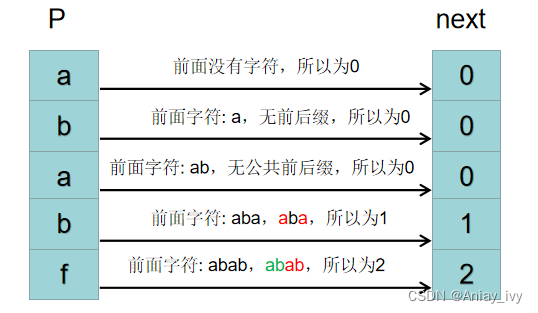
求最长公共前后缀长度的时候，可以用暴力的求法，但效率很低。我们可以用另一种方法来求：

假设已经知道 P[i] 之前的各个字符的最长公共前后缀长度 next[0 ~ i-1]，看看能不能通过 next[0 ~ i-1] 求出 next[i]。

以 P = “ababdababaa” 为例，已知next[8] = 3，求next[9] :

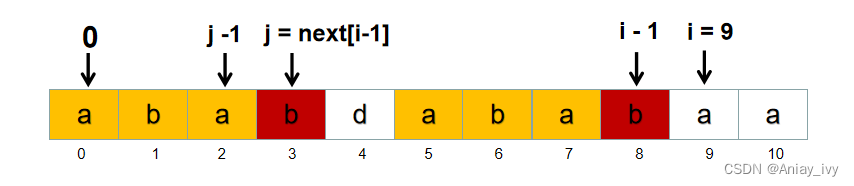
next[8] 等于黄色部分长度：next[8] = 3。含义：P[8] 的最长公共前后缀长度为3，即： P[0 ~ 2] 与 P[5 ~ 7] 相同。根据next的含义，可以得出 P[0 ~ 3] 与 P [4 ~ 7] 不同，所以 P[0 ~ 4] 与 P[4 ~ 8] 不同。因此 next[9] 肯定小于 5。

上图这种情况，next[8] = 3, 即 P[0 ~ 2] 与 P[5 ~ 7] 相同，又因为 P[ next[i-1] ] ( next[i - 1] = 3 ) 与 P[i - 1] (i - 1 = 8) 是相同字母，所以P[0 ~ 3] 与 P[5 ~ 8] 相同。又因为在上一段中，根据 next 的含义，推出了P[0 ~ 4] 与 P[4 ~ 8] 不同。所以next[9] = next[8] + 1 = 4。

可以得出结论：当P[ next[i-1] ] 与 P[i - 1] 是同一个字母的时候，P[i] = P[i-1] + 1。

能严格证明下当P[ next[i-1] ] 与 P[i - 1] 是同一个字母的时候，P[i] = P[i-1] + 1吗？

可以，不过比较烧脑。

当 i >= 3 的时候，若 P[i - 1] = P[ next[i-1] ]，则 next[i] = next[i - 1] + 1，证明如下(烧脑时刻)：

首先用反证法证明： next[i] < next[i - 1] + 2。

假设 next[i] >= next[i - 1] + 2， 令 k = next[i - 1]，t = next[i]， 则 t >= k + 2。因为next[i] = t，所以 P[0 ~ t-1] 与 P[i-t ~ i-1] 相同。又因为 t >= k + 2，所以 t - 2 >= k，i - t =< i - k -2，所以P[0 ~ k] 与 P[i-2-k ~ i-2] 相同，所以next[i - 1] = k + 1，与next[i - 1] = k 矛盾，所以： next[i] < next[i - 1] + 2。

接着证明：若 P[i - 1] = P[ next[i-1] ]，next[i] 大于等于next[i - 1] + 1。

令 k = next[i - 1]，t = next[i]，k 必定大于等于 0 且 小于等于 i - 1，且以P[0 ~ k-1] 与 P[i-1-k ~ i-2] 相同(如果出现下标不合法，则认为为空)。因为P[i - 1] = P[ next[i-1] ]，即P[i - 1] = p[k]， 所以P[0 ~ k] 与 P[i-1-k ~ i-1] 相同，所以next[i] >= next[i - 1] + 1。

综上：若 P[i - 1] = P[ next[i-1] ]，则 next[i] = next[i - 1] + 1。

已经知道了 P[ next[i-1] ] 与 P[i - 1] 相同的时候，next[i] 怎么求。P[ next[i-1] ] 与 P[i - 1] 不同的时候怎么办？

在求 next[10] 的时候就是这种情况，如下图：

先看下 next[10] 怎么求：

因为 P[9] 与 P[4] 不同，所以无法从 next[9] 推导出 next[10]。根据 next[9] = 4 的含义，可以知道，P[0 ~ 3] (“abab”) 与 P[5 ~ 8] (“abab”) 相同。

看一下 next[ next[9] ] = next[4] = 2 的含义：P[0 ~ 1] 与 P[2 ~ 3] 相同，又因为 P[2 ~ 3] 与 P[7 ~ 8] 相同，P[2] 与 P[9] 相同，所以P[0 ~ 3] 与 P[7 ~ 9] 相同，next[10] 大于等于 next[4] + 1 = 3。

因为 next[4] = 2，所以P[0 ~ 2] 与 P[1 ~ 3] 不同(如果相同，next[4] 等于 3 ，与next[4] 等于 2 矛盾)。又因为 P[1 ~ 3] 与 P[6 ~ 8] 相同，所以 P[0 ~ 2] 与 P[6 ~ 8] 不同，所以 P[0 ~ 3] 与 P[6 ~ 9] 不同，所以 next[10] 小于 4。

4 > next[10] >= 3， 所以next[10] 等于 3。

所以当 P[ next[i - 1] ] 与 P[i - 1] 不同的时候，可以这样求 next[i]:

令 j 等于 next[i - 1]，如果 P[j] 与 P[i -1] 不同，一直通过 j = next[j] 更新 j 的值，直到遇到 P[j] 与 P[i - 1] 相同，P[i] 就等于 j + 1。如果 j 的值更新到了 0 ，就不用继续更新了，这时候：如果 P[0] 与 P[i - 1] 相同， next[i] 就等于 1；如果 P[0] 与 P[i - 1] 不同，next[i] 就等于 0。

这一部分是挺烧脑的，毕竟这个算法是集结 Knuth，Morris，Pratt 三位大神合力想出来的。很难通过一次讲解就完全弄明白。最好拿出纸笔，对照例子，手动模拟几遍。下次我来个视频版本的，就容易理解一些了。

给出两个版本的代码，一个是易理解版本的，一个是凝练版本的。

代码

代码一：易理解

//cpp
#include <string>
#include <iostream>

using namespace std;
const int N = 1000010;
string p, s;
int ne[N];//ne是next数组，c++ 中，next在头文件被用过了，我们不能继续使用

int main()
{
    cin >> p >> s;//s: 长字符串，p短字符串
    ne[0] = 0;//初始化ne[0]
    ne[1] = 0;//初始化ne[1]
    for (int i = 2; i < p.size() + 1; i++)
    {
        int j = ne[i - 1];
        while (j && p[i - 1] != p[j])// p[i] 与 P[j] 不同且 j 不为 0，就一直更新 j 为next[j]。
            j = ne[j];//询问上帝
        if (j != 0)//如果 j 不为0，就是 p[i - 1] == p[j] 成立，导致 while 循环结束
            ne[i] = j + 1;
        else//j = 0 导致 while 循环结束
        {
            if (p[j] == p[i - 1]) 
                ne[i] = 1;
            else
                ne[i] = 0;
        }
    }
    for (int i = 0, j = 0; i < s.size(); i++)
    {
        while (j && s[i] != p[j])
            j = ne[j];
        if (s[i] == p[j]) j++;
        if (j == p.size())
        {
            cout << i - j + 1 << " ";
            return 0;
        }
    }
}

代码二：凝练

#include <string>
#include <iostream>

using namespace std;
cnst int N = 1000010;

string p, s;
int ne[N];

int main()
{
    cin >> p >>  s;
    ne[0] = 0;
    ne[1] = 0;
    int i = 2, j = 0;
    for (i = 2; i < p.size() + 1; i++)
    {
        while (j && p[i - 1] != p[j]) j = ne[j];
        if (p[i - 1] == p[j]) j++;
        ne[i] = j;
    }
    for (i = 0, j = 0; i < s.size(); i++)
    {
        while (j && s[i] != p[j]) j = ne[j];
        if (s[i] == p[j]) j++;
        if (j == p.size())
        {
            cout << i - j + 1 << " ";
            return 0;
        }
    }
}

Java

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Scanner;
public class Main{
    static int N = 100010;
    static int ne[] = new int[N];
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        Integer n = Integer.parseInt(br.readLine());
        String s1 = " " + br.readLine();
        Integer m = Integer.parseInt(br.readLine());
        String s2 = " " + br.readLine();
        char[] a1 = s1.toCharArray();
        char[] a2 = s2.toCharArray();
        /**
         * ne[]：存储一个字符串以每个位置为结尾的‘可匹配最长前后缀’的长度。
         * 构建ne[]数组：
         *              1,初始化ne[1] = 0,i从2开始。
         *              2,若匹配，s[i]=s[j+1]说明1~j+1是i的可匹配最长后缀,ne[i] = ++j;
         *              3,若不匹配，则从j的最长前缀位置+1的位置继续与i比较
         *              (因为i-1和j拥有相同的最长前后缀，我们拿j的前缀去对齐i-1的后缀),
         *              即令j = ne[j],继续比较j+1与i，若匹配转->>2
         *              4,若一直得不到匹配j最终会降到0，也就是i的‘可匹配最长前后缀’的长度
         *              要从零开始重新计算
         */
        for(int i = 2,j = 0;i <= n ;i++) {
            while(j!=0&&a1[i]!=a1[j+1]) j = ne[j]; 
            if(a1[i]==a1[j+1]) j++;
            ne[i] = j;
        }
        /**
         * 匹配两个字符串：
         *      1，从i=1的位置开始逐个匹配，利用ne[]数组减少比较次数
         *      2，若i与j+1的位置不匹配（已知1~j匹配i-j~i-1)，
         *      j跳回ne[j]继续比较(因为1~j匹配i-j~i-1,所以1~ne[j]也能匹配到i-ne[j]~i-1)
         *      3，若匹配则j++,直到j==n能确定匹配成功
         *      4，成功后依然j = ne[j],就是把这次成功当成失败，继续匹配下一个位置
         */
        for(int i = 1,j = 0; i <= m;i++) {
            while(j!=0&&a2[i]!=a1[j+1]) j = ne[j];
            if(a2[i]==a1[j+1]) j++;
            if(j==n) {
                j = ne[j];
                bw.write(i-n+" ");
            }
        }
        /**
         * 时间复杂度：
         *      因为：j最多加m次，再加之前j每次都会减少且最少减一，j>0
         *      所以：while循环最多执行m次,若大于m次，j<0矛盾
         *      最终答案：O(2m)
         */
        bw.flush();
    }
}

时间上，长字符串遍历一遍，短字符串遍历一遍，所以时间复杂度是 O(n + m)；开辟了一个与短字符串相关的 next 数组，空间复杂度是 O(m) m 。