前缀和与差分算法总结（C语言）

已于 2024-04-20 15:03:39 修改
阅读量1k 收藏 32
点赞数 24
文章标签： c语言 算法 数据结构
于 2023-11-26 18:03:25 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Patrick_yuxuan/article/details/134629752
版权

欢迎来到我的博客

文章目录

一维前缀和

基本原理

前缀和算法是一种通过预处理数组元素，计算从数组起始位置到当前位置的累积和的方法。这样，我们可以在O(1)时间内获取任意区间的和。

给出一个数组int nums[5] = {1, 2, 3, 4, 5}

它的前缀和为int presum[5] = {1, 3, 6, 10, 15}

即{ 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, 1 + 2 + 3 + 4 + 5}

int main() {
	int nums[5] = { 1, 2, 3, 4, 5 };
	int presum[5] = { 1, 3, 6, 10, 15 };
	presum[0] = nums[0];
	for (int i = 1; i < 5; i++) {
		presum[i] = nums[i] + presum[i - 1];
	}
}

用途

1.求数组前n个数之和

求数组前三个数之和：presum[2]

求数组所有数之和：presum[n - 1]

2.求数组区间和

[L,R]---->presum[R] - presum[L - 1]

presum[L - 1] 指 nums 数组中的nums[L - 1]前面所有数字之和（包括它自己）

preSum[R]表示的是 nums数组中num[R]前面所有数字之和（包括它自己）

例如我们想求解nums数组第2到4个数的区间和，也就是nums数组对应nums[1] 到nums[3]的区间，我们只需使用presum[3] - presum[1 - 1]即可得到

    int nums[5] = { 1, 2, 3, 4, 5 };
	int presum[5] = { 1, 3, 6, 10, 15 };

presum[3] - presum[0] = (1 + 2 + 3 + 4)-(1)

相减得到2 + 3+ 4

例题
643. 子数组最大平均数 I

给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。

请你找出平均数最大且 长度为 k 的连续子数组，并输出该最大平均数。

任何误差小于 10-5 的答案都将被视为正确答案。

double findMaxAverage(int* nums, int numsSize, int k) {
    // 计算前缀和
    int* presum = (int*)malloc(numsSize * sizeof(int));
    presum[0] = nums[0];
    for (int i = 1; i < numsSize; ++i) {
        presum[i] = presum[i - 1] + nums[i];
    }
    // 初始化最大值为前 k 个元素的和
    int max = presum[k-1];
    // 使用前缀和计算子数组的和
    for (int i = 0; i < numsSize - k; ++i) {
        max = fmax(presum[i + k] - presum[i], max);
    }
    free(presum);
    return (double)max / k;
}

二维前缀和

基本原理

二维前缀和实际上是一个新的二维数组，其中每个元素表示原始矩阵中左上角元素到当前元素的所有元素的和。

1  2   3         1  3  6
4  5   6         5  12  21
7  8   9        12   27  45

二维前缀和数组公式：

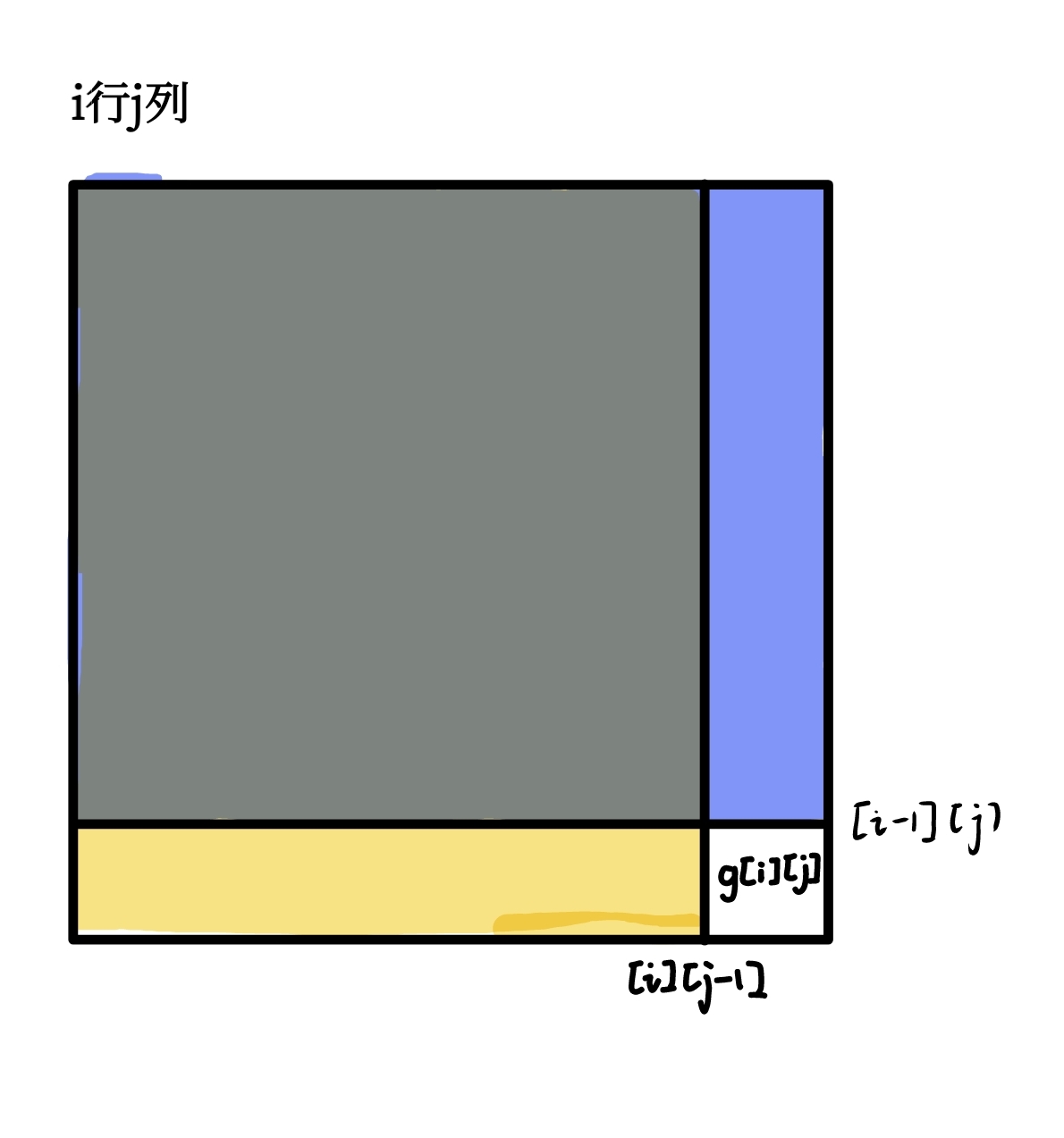
prefixSum[i][j] = matrix[i][j] + prefixSum[i−1][j] + prefixSum[i][j−1] - prefixSum[i−1][j−1]

prefixSum[i−1][j]：上方元素 (i-1, j) 在 prefixSum 中的值。
prefixSum[i][j−1]：左方元素 (i, j-1) 在 prefixSum 中的值.
prefixSum[i−1][j−1]：左上方元素 (i-1, j-1) 在 prefixSum 中的值。

在这里插入图片描述

边界问题，需要特判
当(i=0,j=0) prefixSum[0][0] = matrix[0][0]
当i = 0 prefixSum[0][j] = prefixSum[0][j-1] + matrix[0][j]
当j = 0 prefixSum[i][0] = prefixSum[i-1][0] + matrix[i][0]

用途

求二维数组区间和

给出公式
sum[x1,y1][x2,y2] = sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1]

在这里插入图片描述

当(i=0,j=0) Sum[0,0][0,0] = matrix[0,0]
当x = 0 Sum[0,y1][0,y2] = Sum[0][y2] - Sum[0][y1-1]
当y=0 Sum[x1,0][x2,0] = Sum[x1][0] - Sum[x2-1][0]

例题

计算【1，1】【2，3】之间数字和

1  2  3  4
5  6  7  8
9  10 11 12

计算出前缀和数组

1  3  6  10
6  14 24 36
15 33 54 78

sum[2][3] - sum[2][0] - sum[0][3] + sum[0,0]
78-15-10+1 = 54
给出以下代码供参考

#include <stdio.h>
int calculateRegionSum(int prefixSum[4][5], int row_start, int row_end, int col_start, int col_end) {
    return prefixSum[row_end + 1][col_end + 1] - prefixSum[row_start][col_end + 1]
        - prefixSum[row_end + 1][col_start] + prefixSum[row_start][col_start];
}
int main() {
    int matrix[3][4] = {
        {1, 2, 3, 4},
        {5, 6, 7, 8},
        {9, 10, 11, 12}
    };
    // 创建一个数组存储前缀和
    int prefixSum[4][5] = { 0 };
    // 计算前缀和数组
    for (int i = 1; i <= 3; i++) {
        for (int j = 1; j <= 4; j++) {
            prefixSum[i][j] = matrix[i - 1][j - 1] + prefixSum[i - 1][j] 
                              + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1];
        }
    }
    int sum = calculateRegionSum(prefixSum, 1, 2, 1, 3);
    printf("%d\n", sum);
    return 0;
}

一维差分

差分算法的核心思想是将原始数组转化为差分数组，
其中差分数组的每个元素表示原始数组中相邻元素之差
这种转换可以使得在原数组的某个区间内进行批量更新变得非常高效。

基本原理

差分数组 diff 通过以下方式计算：

for (int i = 1; i < n; ++i) {
    diff[i] = nums[i] - nums[i-1];
}

diff[i] 就表示原数组 nums[i] 和 nums[i-1] 之差
例如
nums[5] = { 1, 5, 8, 9, 6 };
diff[5] = { 1, 4, 3, 1, -3 };
pre[5] = {1, 5 ,8 ,9 ,6}
差分数组的前缀和就是原数组

用途

1.区间增量

给定数组 nums，需要在某个区间 [start, end] 内的所有元素增加一个常量值 val。

diff[start] += val; 
diff[end + 1] -= val;

差分数组中还原成原数组的时候start后面的数都会累加,然后再end+1位在减去这个数停止累加

diff[start] += val; 使得presum[start]后面都加上了val,
diff[end + 1] -= val;同理使presum[end + 1]后面都减去val，
相当于
presum[start]~presum[end] +val
presum[end+1]~presum[lenth-1]+val-val
相当于
在区间 [start, end] 内的所有元素增加一个常量值 val。

接下来我们只需遍历一次差分数组根据前缀和计算就得到更新后的数组。

例如
nums[5] = { 1, 5, 8, 9, 6 }
diff[5] = { 1, 4, 3, 1, -3 }
对以下两个区间内数加val
[1, 3] + 2 ------- diff[1]+=2 diff[4]-=2 ------- diff[5] = { 1, 6, 3, 1, -5 }
[2, 4] + 3 ------- diff[2]+=3 diff[5]-=3 ------- diff[5] = {1, 6, 6, 1, -5 }
diff[5] = {1, 6, 6, 1, -1 }
pre[5] = {1, 7, 13, 14, 9}

这里给出上述例子代码供参考

#include <stdio.h>
void DiffArray(int diff[], int start, int end, int val) {
    diff[start] += val;
    if (end + 1 < 5) {
        diff[end + 1] -= val;
    }
}
int main() {
    int nums[] = { 1, 5, 8, 9, 6 };
    int diff[] = { 1, 4, 3, 1, -3 };
    int presum[5];
    DiffArray(diff, 1, 3, 2);// 区间 [1, 3] 加 2
    DiffArray(diff, 2, 4, 3);// 区间 [2, 4] 加 3
    presum[0] = diff[0];
    for (int i = 1; i < 5; ++i) {
        presum[i] = presum[i - 1] + diff[i];
    }
    for (int i = 0; i < 5; ++i) {
        printf("%d ", presum[i]);
    }
    return 0;
}

二维差分

基本原理

d[x1][y1] += val
d[x2+1][y1] -= val
d[x1][y2+1] -= val
d[x2+1][y2+1] += val
在这里插入图片描述

用途

对以下数组做如下处理
[0,0][2,1]+3
[1,1][2,2]-1

1  2  3  4
5  6  7  8
9  10 11 12

先差分标记[0,0][2,1]+3

3  0 -3  0  0
0  0  0  0  0
0  0  0  0  0
-3 0  3  0  0

再标记 [1,1][2,2]-1

3   0  -3   0  0
0  -1   0   1  0
0   0   0   0  0
-3  1   3  -1  0

计算前缀和

3  3  0  0  0
3  2 -1  0  0
3  2 -1  0  0
0  0  0  0  0

将该数组对应加到原数组

4  5  3  4
8  8  6  8
12 12 10 12

得到答案
给出如下代码供参考：

#include <stdio.h>

void add(int d[4][5],int matrix[3][4], int x1, int y1, int x2, int y2, int val) {
    d[x1][y1] += val;
    d[x2 + 1][y1] -= val;
    d[x1][y2 + 1] -= val;
    d[x2 + 1][y2 + 1] += val;
}
int main() {
    int matrix[3][4] = {
        {1, 2, 3, 4},
        {5, 6, 7, 8},
        {9, 10, 11, 12}
    };
    int d[4][5] = { 0 };
    add(d,matrix, 0, 0, 2, 1, 3);
    add(d,matrix, 1, 1, 2, 2, -1);
    int prefixSum[4][5] = { 0 };
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 5; j++) {
            if (i == 0 && j == 0) {
                prefixSum[0][0] = d[0][0];
            } else if (i == 0 && j!=0){
                prefixSum[0][j] = prefixSum[0][j - 1] + d[0][j];
            } else if (i != 0 && j == 0) {
                prefixSum[i][0] = prefixSum[i - 1][0] + d[i][0];
            }
            else {
                prefixSum[i][j] = d[i][j] + prefixSum[i - 1][j]
                    + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1];
            }
        }
    }
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 4; j++) {
            matrix[i][j] += prefixSum[i][j];
        }
    }
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 4; j++) {
            printf("%d ", matrix[i][j]);
        }
        printf("\n");
    }
    return 0;
}

感谢您的阅读

去看全世界的云
关注
  • 24
    点赞
  • 踩
  • 32
    收藏
    觉得还不错? 一键收藏
  • 2
    评论
基于C语言实现前缀和算法（源码）
03-31
前缀和（Prefix Sum）是一种常用的技巧，用于快速计算数组中某个区间内元素的和。其基本思想是先计算出数组中每个位置的前缀和，然后通过前缀和的差值来求得任意区间的和。
前缀和与差分算法地深入理解
07-11
该内容包括：一维前缀和、二维前缀和、差分和差分矩阵
前缀和与差分
邓汪涛的博客
01-16 454
文章目录前缀和1. 前缀和2. 子矩阵的和差分1. 差分2. 差分矩阵 前缀和 1. 前缀和 输入一个长度为n的整数序列。 接下来再输入m个询问，每个询问输入一对l, r。 对于每个询问，输出原序列中从第l个数到第r个数的和。 输入格式 第一行包含两个整数n和m。 第二行包含n个整数，表示整数数列。 接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。 输出格式 共m行，每行输出一个询问的结果。 数据范围 1≤l≤r≤n1≤l≤r≤n1≤l≤r≤n 1≤n,m≤1000001≤n,m≤100000
前缀和与差分算法
m0_61705102的博客
01-06 2839
前缀和与差分一维前缀和一维差分二维前缀和二维差分 一维前缀和 先看一个例子，假如我们现在有一个数组 arr[]={3,2,5,6,7,8,9,4,2} 现在假如我们要想的得到区间 [ 3 , 6 ]，上的数据和，那我们就需要遍历 [ 3 , 6 ] 这个区间进行求和。 代码如下： #include <stdio.h> int main() { int arr[] = { 3,2,5,6,7,8,9,4,2 }; int sum = 0; int l, r; scanf("%d%d",
前缀和与查分（一维前缀和，二维前缀和（子矩阵的和）一维差分、二维差分（差分矩阵））
qq_59702185的博客
09-02 565
百度给的定义就是：前缀和表示一个序列的前n项和，理解为数组的话就是从下标为1到n（定义成数组时就从下标为1开始接收该序列），而差分就是前缀和的逆运算，前缀和与差分数组是对应关系。前缀和就是指某个序列的前n项和，类似于数列的求n项和。我们前缀和一般都是从a1开始，默认初始值a0的值为0；那么前缀和的公式就是：s(i) = a(1) + a(2) + ……+ a(i);原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]前缀和 Si为数组的前 i项和。
差分与前缀和
m0_62878102的博客
04-10 1440
前言 酝酿好久的第一篇博客，缺点不少，多多指教吖。 目录 算法原理 算法图解 核心代码 实战应用 正文 一、算法原理 差分和前缀和算法的核心或可浓缩成以下等式： a[i]=s[i]-s[i-1] 它是利用差分数组和前缀和数组的对应关系，改变其中之一，而影响另一的算法。前缀和可以理解为数学中数列的前n项和，而差分则是其逆过程。 前缀和数组：用以存储已知数组的前n项和，设为s，其中s[i]存放已知数组的前i项和。 ...
算法——前缀和及差分
scfor333的博客
03-23 496
前缀和及差分 ​ 前缀和与差分是互为逆运算的两种计算方式，前缀和指的是一个数组是另一个数组中前n项元素之和，而差分指的是一个数组的前n项的和是另一个数组 ​ 实际上就是，如果数组a是数组b的前缀和，那b就是a的差分 前缀和 ​ 根据如上的的解释，我们可以理解为，假设有数组a为[1, 2, 3, 4, 5]那么代表它的前缀和数组的数组b就是1, 3, 6, 10, 15，也就是说，a[n] ...
某学长讲课ppt（前缀和与差分，二维前缀和与差分）
03-23
一、内容概述 本资源是一份详尽的关于前缀和与差分的PPT制作素材，旨在帮助使用者通过视觉化的方式，全面而深入地理解这两个在...总结与回顾：对整个PPT内容进行总结，强调前缀和与差分的重要性，鼓励大家在实际编程
前缀和与差分作业.pdf
04-22
前缀和与差分作业.pdf
常见数据结构与算法C语言实现
05-04
# 常见数据结构与算法C语言实现 内容包含常见基本数据结构实现（C语言版）如各自排序、链表、栈、队列、各种树以及应用、图算法、字符串匹配算法、回溯、并查集等 以及包含各个数据结构常见算法题的解答（C语言版...
算法----前缀和与差分
chl3518的博客
02-21 899
输出结果为：1 3 6 10 15这个示例代码定义了一个函数prefixSum，输入参数为一个整数数组arr，输出一个整数数组prefix，存储了arr的前缀和。首先创建一个和arr大小相同的数组prefix，将arr的第一个元素赋值给prefix的第一个元素。然后使用遍历的方式计算prefix的其他元素。从索引 1 开始遍历arr，依次计算每个元素的前缀和，即。这里使用了前一个元素的前缀和加上当前元素的值来计算当前元素的前缀和。最后，在main函数中，定义了一个整数数组arr。
C/C++ 前缀和与差分
敲代码嘞~的博客
12-06 764
前缀和就更像是数学中的前n项和。比如说数组【1，1，1，1，1】，则前缀和数组就是【1，2，3，4，5】。差分更像是前缀和数组的原数组。比如说前缀和数组是【1，2，3，4，5】，则差分数组就是【1，1，1，1，1】。总结一句话：前缀和和差分是互逆运算。
前缀和与差分（较详细）【算法基础】
rank_fei的博客
12-18 363
！前缀和与差分。
数据结构——二叉树（C语言版）
最新发布
2302_80657849的博客
05-30 591
二叉树是一种非线性的数据结构。二叉搜索树、堆、红黑树等高阶数据结构都是依托于二叉树的基础实现的，所以我们有必要好好研究一下“二叉树”这种数据结构。本文只介绍二叉树的基础及中等用法，笔者能力有限，欠妥当之处欢迎批评指正。
二叉排序树简单实现【C风格】
weixin_45690131的博客
05-30 106
利用二叉排序树对数据进行保存、搜索、删除
Leecode---347：输出前k个高频元素（使用unordered_map）
qq_41920323的博客
05-30 180
unordered_map实现输出前k个高频元素
算法每日一题（python,2024.05.24) day.6
L613Z的博客
05-27 416
数字比较型可以用双指针法寻找数字相同（或构成其他关系）的俩个数值（或其他类型），涉及到与数值有关的列表问题可以思考到sort()排序方法加以辅助。
并查集拓展（扩展域并查集）
Qlarkstar的博客
05-29 762
事实证明，扩展域并查集应该在带权并查集前面讲的，因为比较好理解，而且回过头看带权并查集可能也会更轻松一些。
前缀和与差分（超详细！！！）
06-07
前缀和和差分是一类常用的算法，它们常常被用来优化一些区间操作的问题，如求区间和、区间最大值/最小值等等。下面我们将分别介绍前缀和和差分的定义、用法和常见问题。 ## 前缀和 前缀和，顾名思义，就是把前面所有数的和都求出来，用一个数组存起来，以便之后的查询。 ### 定义 给定一个长度为 $n$ 的序列 $a$，令 $s_i = \sum_{j=1}^{i}a_j$，则 $s$ 称为序列 $a$ 的前缀和数组。 ### 用法 前缀和的主要作用是用 $O(1)$ 的时间复杂度求出一个区间 $[l,r]$ 的和，即 $s_r - s_{l-1}$。这是因为 $s_r$ 存储了序列从 $1$ 到 $r$ 的和，而 $s_{l-1}$ 存储了序列从 $1$ 到 $l-1$ 的和，因此区间 $[l,r]$ 的和可以通过两个前缀和相减计算得出。 前缀和的时间复杂度为 $O(n)$，因为需要遍历一遍序列求出前缀和数组。但是，如果有多个查询需要求区间和，那么使用前缀和可以将每次查询的时间复杂度降低到 $O(1)$。 ### 代码实现 下面是使用前缀和求区间和的代码实现： ```cpp vector<int> a; // 原序列 vector<int> s(a.size() + 1); // 前缀和数组 // 计算前缀和 for (int i = 1; i <= a.size(); i++) { s[i] = s[i - 1] + a[i - 1]; } // 查询区间 [l, r] 的和 int sum = s[r] - s[l - 1]; ``` ## 差分 差分和前缀和相反，它主要用来对区间进行修改。我们可以利用差分数组进行区间修改，并最终得到修改后的序列。 ### 定义 给定一个长度为 $n$ 的序列 $a$，令 $d_i = a_i - a_{i-1}$（$d_1 = a_1$），则 $d$ 称为序列 $a$ 的差分数组。 ### 用法 差分的主要作用是对区间进行修改。假设我们需要将区间 $[l,r]$ 的数加上 $k$，我们可以将差分数组的 $d_l$ 加上 $k$，将 $d_{r+1}$ 减去 $k$。这样，对差分数组求前缀和，就可以得到修改后的序列。 具体来说，我们可以按照以下步骤进行区间修改： 1. 对差分数组的 $d_l$ 加上 $k$； 2. 对差分数组的 $d_{r+1}$ 减去 $k$； 3. 对差分数组求前缀和，得到修改后的序列。 差分的时间复杂度为 $O(n)$，因为需要遍历一遍序列求出差分数组。但是，如果有多次区间修改需要进行，那么使用差分可以将每次修改的时间复杂度降低到 $O(1)$。 ### 代码实现 下面是使用差分进行区间修改的代码实现： ```cpp vector<int> a; // 原序列 vector<int> d(a.size() + 1); // 差分数组 // 计算差分数组 for (int i = 1; i < a.size(); i++) { d[i] = a[i] - a[i - 1]; } // 修改区间 [l, r]，将数加上 k d[l] += k; d[r + 1] -= k; // 对差分数组求前缀和，得到修改后的序列 for (int i = 1; i < d.size(); i++) { a[i] = a[i - 1] + d[i]; } ``` ## 常见问题 ### 1. 差分数组的长度是多少？ 差分数组的长度应该比原序列长度多 1，因为 $d_1 = a_1$。 ### 2. 什么情况下使用前缀和？什么情况下使用差分？ 如果需要进行多次区间查询，那么使用前缀和可以将每次查询的时间复杂度降低到 $O(1)$；如果需要进行多次区间修改，那么使用差分可以将每次修改的时间复杂度降低到 $O(1)$。 ### 3. 前缀和和差分的本质区别是什么？ 前缀和和差分都是用来优化区间操作的算法，它们的本质区别在于： - 前缀和是通过预处理前缀和数组来优化区间查询； - 差分是通过预处理差分数组来优化区间修改。 ### 4. 前缀和和差分能否同时使用？ 当然可以。如果需要同时进行区间查询和修改，我们可以先使用差分数组对区间进行修改，然后再对差分数组求前缀和，得到修改后的序列。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值