一文详解:堆、堆排序、topK问题及优先级队列

leaf-view

已于 2024-05-28 20:31:09 修改

阅读量1.4k

点赞数 50

文章标签： c++ c语言排序算法数据结构

于 2024-05-28 20:28:54 首次发布

本文链接：https://blog.csdn.net/Pau_0618/article/details/139266741

版权

一、前置知识

什么是堆？

如果有一个关键码的集合K={k0, k1, k2, …, kn}，它这些关键码按照完全二叉树的顺序存储方式存储到一维数组中，且满足：父节点的值<=子节点的值（或者父节点的值>=子节点的值），则称为小顶堆（或者大顶堆）。

堆的性质

父节点的值<=子节点的值（或者父节点的值>=子节点的值）
堆是一颗完全二叉树

父子下标关系

堆的节点是可以存储于数组或者链表中的，若存储于数组中则有如下的坐标关系：
已知父节点下标，找孩子节点下标：
左孩子下标 = 父亲下标 * 2 + 1
右孩子下标 = 父亲下标 * 2 + 2
已知孩子节点下标，找父节点下标：
父亲下标 = (孩子下标 - 1) / 2
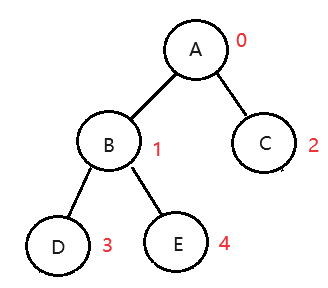
在这里插入图片描述

堆的定义

typedef int HPDataType;
class Heap{
    HPDataType* a;
    int size;
    int capacity;
}HP;
void HeapInit(HP* php)
{
    assert(php);
    php->a = NULL;
    php->size = php->capacity = 0;
}
void HeapDestroy(HP* php)
{
    assert(php);
    free(php->a);
    php->a = NULL;
    php->size = php->capacity = 0;
}

上滤操作(以大堆为例)

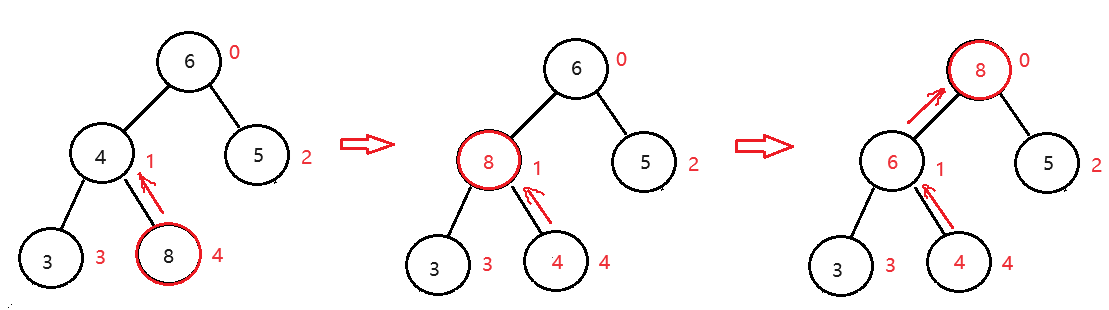
在这里插入图片描述
子节点只需要和它的父节点去比较即可，比较完后继续往上遍历。

void Swap(int* p1, int* p2) 
{    inttemp = *p1;     
	*p1 = *p2;     
	*p2 = temp; 
}
// a：参与上滤操作的数组  n：开始上滤的起始位置 
void AdjustUp(int* a, int n) 
{
	int children = n;     
	int parents = (children - 1)/2;     
	while(children > 0)     
	{         
		// 按大堆规则判断         
		if(a[children] > a[parents])         
		{             
			Swap(&a[children], &a[parents]); // 交换父子             
			children = parents;            // 继续往上找父子关系，判断是否要交换             
			parents = (children - 1)/2;         
		}         
		else break; // 不满足交换条件就退出循环，因为前面的已经满足了堆的条件         
	}
}

时间复杂度：O(logN)
每遍历一个数据都要和父亲去比较大小，时间复杂度体现在父亲节点和子节点比较的次数，即二叉树的层数O(logN)。

下滤操作(以大堆为例)

在这里插入图片描述
画图很容易，但实际上下滤比上滤要麻烦。因为上滤比较的节点只有一个，而下滤比较的节点有两个，分别是左右孩子，比较的原则是：如果是大顶堆，那么就和较大的孩子去比较，让较大的孩子往上挪；如果是小顶堆，那么就和较小的孩子去比较，让较小的孩子往上挪。

// a：参与下滤操作的数组  n：开始下滤的起始位置  size：数组的大小
// 说明：左孩子是一定有的，但右孩子不一定有，且最后一个节点要么是左孩子要么是右孩子
// 后面在进行更新左孩子时要注意判断右孩子是否存在。
void AdjustDown(int* a, int n, int size)
{
    int parents = n;
    int children = 2*parents + 1;
    while(children < size)
    {
        if(children + 1 < size
            && a[children + 1] > a[children])  // 以大堆为例,如果右孩子更大则更新左孩子
        {
            children++;
        }
        if(a[children] > a[parents])           // 和较大的孩子进行交换
        {
            Swap(&a[children], &a[parents]);
            parents = children;// 由于子节点改变了，原来的堆关系也可能发生改变，继续往下找父子关系，判断
            children = 2*parents + 1;// 是否要交换
        }
        else break;
    }
}

时间复杂度：O(logN)
每遍历一个数据都要和孩子去比较大小，时间复杂度体现在父亲节点和子节点比较的次数，即二叉树的层数O(logN)。

二、堆的插入

在二叉树的尾部插入节点，注意考虑扩容问题，然后使用上滤操作处理二叉树使其称为大顶堆。

// 堆的插入 时间复杂度：O(logN)
// php：结构体指针，负责改变结构体内部的数据  x：要插入的数据
void HeapPush(HP* php, int x)
{
    assert(php);
    /* ----------------------判断空间是否足够------------------ */
    if(php->size == php->capacity)
    {
        int newcapacity = php->capacity == 0 ? 4 : 2*php->capacity;
        int * newnode = (int *)realloc(php->a, sizeof(int)*newcapacity);
        if(newnode == NULL)
        {
            perror("realloc fail");
            return;
        }
        php->capacity = newcapacity, php->a = newnode;
    }
    /* -------------------------------------------------------- */
    php->a[php->size++] = x;
    AdjustUp(php->a, php->size - 1);  // 从最后一个元素开始上滤
}

时间复杂度：O(logN)
每插入一个数据都要和父亲去比较大小，时间复杂度就是上滤的时间复杂度O(logN)。

二、堆的删除

堆的删除指的是删除堆顶元素。具体做法是将要删除的元素和最后一个叶子结点进行交换，再删除最后一个叶子结点即可。最后别忘了用下滤重新调整这个二叉树。

// 删除堆顶元素
void HeapPop(HP* php)
{
    assert(php);
    Swap(&php->a[0], &php->a[php->size-1]);
    php->size--;
    AdjustDown(php->a, 0, php->size);
}

时间复杂度：O(logN)
从上往下遍历数据都要和孩子去比较大小，时间复杂度就是下滤的时间复杂度O(logN)。
注意：插入用上滤，删除用下滤，原则就是从要处理的新元素开始往上还是往下调整。

三、三种建堆方案

通过插入元素建堆(不推荐)

通过插入元素建堆，每插入一个元素就要上滤调整二叉树。

// 建堆的时间复杂度 O(NlogN)
void testheap1()         
{
    HP hp;
    HeapInit(&hp);
    HeapPush(&hp, 1);   // 插入的过程中就已经完成了上滤操作
    HeapPush(&hp, 6);
    HeapPush(&hp, 5);
    HeapPush(&hp, 2);
    HeapPush(&hp, 10);
    HeapPush(&hp, 19);
    HeapPush(&hp, 2);
    HeapDestroy(&hp);
}

时间复杂度的计算：

层数	每个节点上滤的层数	第h层的总节点数	所有节点上滤的层数
1	0	2^0	0 * 2^0
2	1	2^1	1 * 2^1
3	2	2^2	2 * 2^2
…	…	…	…
h-1	h-2	2^(h-2)	(h-2) * 2^(h-2)
h	h-1	2^(h-1)	(h-1) * 2^(h-1)

建堆时间复杂度的计算：
F(N) = 0 * 2^0 + 1 * 2^1 + 2 * 2^2 + … + (h-2) * 2^(h-2) + (h-1) * 2^(h-1) …………(1)
2*F(N) = 0 * 2^1 + 1 * 2^2 + 2 * 2^3 + … + (h-2) * 2^(h-1) + (h-1) * 2^(h) …………(2)

(2)-(1):F(N) = - 1 * 2^1 - 1 2^2 - 12^3 - … - 1 * 2^(h-1) + (h-1) * 2^(h)
=−(2 ∗ (1−2^(h1) )) / (1−2) + (h-1) * 2^h
=2 - 2^h + h * 2^h - 2^h
=2^h * (h-2) + 2

假设树有N个节点：则有2^h - 1 = N，可推出h = log(N+1)
所以上式：F(N) = (N+1) * (log(N+1)-2) + 2 ≈ N * log(N)

已有数组，通过上滤建堆(不推荐)

从第二个节点开始往上调整

// 时间复杂度：O(NlogN)
// 在已有数组的情况下，分别对二叉树的每一个节点进行上滤操作
for(int i = 1; i < size; ++i)
{
    AdjustUp(php->a, i);
}

时间复杂度和第一种方式其实是一样的。

已有数组，通过下滤建堆(推荐)

叶子结点无需下滤，所以从倒数第二行开始，向下调整。

// 时间复杂度：O(N)
// 建大堆
for(int i = (size-1-1) / 2; i >= 0; --i) // 从倒数第二行开始，向下调整，叶子结点无需下滤
{
    AdjustDown(php->a, i, size);
}

时间复杂度的计算：

层数	每个节点下滤的层数	第h层的总节点数	所有节点下滤的层数
1	h-1	2^0	h-1 * 2^0
2	h-2	2^1	h-2 * 2^1
3	h-3	2^2	h-3 * 2^2
…	…	…	…
h-1	1	2^(h-2)	1 * 2^(h-2)
h	0	2^(h-1)	0

建堆时间复杂度的计算：
F(N) = (h-1) * 2^0 + (h-2) * 2^1 + (h-3) * 2^2 + … + 1 * 2^(h-2) + 0 * 2^(h-1) …………(1)
2 * F(N) = (h-1) * 2^1 + (h-2) * 2^2 + (h-3) * 2^3 + … + 1 * 2^(h-1) + 0 * 2^(h) …………(2)

(2)-(1):F(N) = -(h-1) * 2^0 + 1 * 2^1 + 1 * 2^2 + 1 * 2^3 + … + 1 * 2^(h-1) (h)
=-(h-1) * 2^0 + (2 ∗ (1−2^(h1) )) / (1−2)
=1 - h + 2^h - 2
=2^h - h - 1

假设树有N个节点：则有2^h - 1 = N，可推出h = log(N+1)
所以上式：F(N) = N+1 - log(N+1) - 1
= N - log(N+1)

四、堆排序

排降序：要建立小堆，取堆顶元素，和叶子结点进行收尾交换，最后一个节点不看做堆里面的，然后下滤选出次小的节点；…重复上面的操作
代码如下（示例）：

// 时间复杂度 O(N + NlogN)
// a为要排序数组
void HeapSort(int* a, int size)
{
    // 建立小堆 -> 时间复杂度:O(N)
    for(int i = (size-1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(a, i, size);
    }
    // 降序排列 -> 时间复杂度:O(NlogN)
    for(int i = size-1; i > 0; i--)
    {
        Swap(&a[0], &a[i]);
        AdjustDown(a, 0, i);
    }
}

总结

堆排序使用堆来选数，效率就高了很多。
时间复杂度：建堆O(N) 排序O(N*logN)
空间复杂度：O(1)
稳定性：不稳定

应用

topK问题

topK问题： 求数据中的前K个最大元素或者最小元素，一般情况下数据量都很大。
可以先排序，再取前k个吗？如果数据量非常大，第一数据可能不能一下子全部加载到内存，第二对整个数据进行排序，再取前K个，这样的代价太大了。
基本思路如下：

用数据集合中的前k个元素来建堆

求前k个最大元素，则建小堆
求前k个最小元素，则建大堆

将剩余的N-K个元素和堆顶元素比较，若要建立小堆，如果比堆顶元素大，则替换堆顶元素进堆；若要建立大堆，如果比堆顶元素小，则替换堆顶元素进堆。
剩余的N-K个元素与堆顶元素比较完之后，堆中的k个元素即为所求。

void PrintTopK(int k)
{
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");//以读的方式打开文件
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}
	//将文件中的前k个数放在数组里面
	int* kminheap = (int*)malloc(sizeof(int) * k);
	if (kminheap == NULL)
	{
		perror("malloc fail");
		return;
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &kminheap[i]);
	}
	
	//建小堆
	for (int i = (k - 1 - 1)/2; i > 0; i--)
	{
		AdjustDown(kminheap, i, k);
	}
	//读取剩下的n-k个值
	int val = 0;
	while (!feof(fout))
	{
		fscanf(fout, "%d", &val);
		// val比堆顶元素大
		if (val > *kminheap)
		{
			*kminheap = val; // 替换堆顶元素
			AdjustDown(kminheap, 0, k);
		}
	}
	
	for (int i = 0; i < k; i++)
	{
		printf("%d\n", kminheap[i]);
	}
}

C++STL 之 priority_queue

在这里插入图片描述
模板参数：
T：容器中元素的类型。
Container： 存储元素的内部底层容器对象的类型。默认缺省容器是vector，STL中的栈和队列不被归纳为容器，而是一种容器适配器(container adapter)，它的底层容器实现可以是数组，可以是链表。
Compare： 一种二进制谓词，它将两个元素（T类型）作为参数并返回布尔。
表达式comp（a，b），其中comp是这种类型的对象，a和b是容器中的元素，如果在函数定义的严格弱排序中a被认为在b之前，则应返回true。
priority_queue使用此函数来维护以保留堆属性的方式排序的元素（即，根据这种严格的弱排序，弹出的元素是最后一个）。
这可以是函数指针或函数对象，默认为 less＜T＞，返回的值与应用小于运算符（a＜b）相同。

使用实例

我要打印升序，默认less为大顶堆
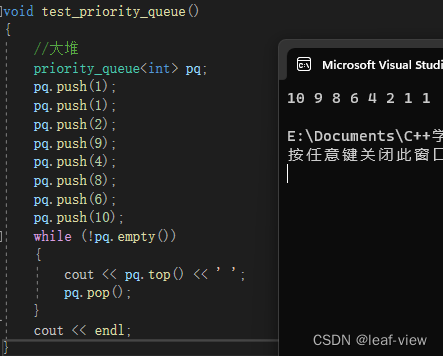
在这里插入图片描述
greater为小顶堆

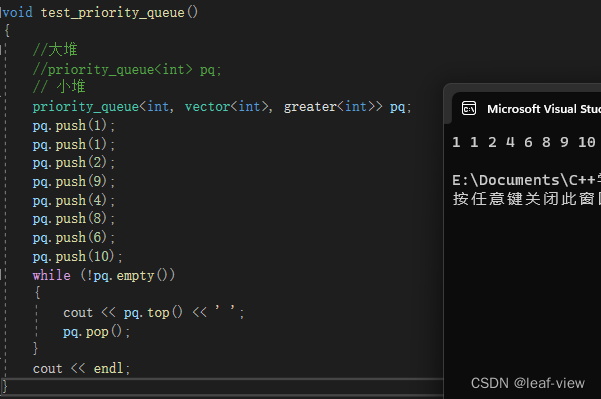
模拟实现

使用容器适配器，可以控制优先级队列的底层容器是数组还是链表；使用仿函数可以控制大小顶堆。

template<class T>
struct less
{
    bool operator()(const T& x, const T& y)
    {
        return x < y;
    }
};
template<class T>
struct greater
{
    bool operator()(const T& x, const T& y)
    {
        return x > y;
    }
};

template <class T, class container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
    void push(const T& x)
    {
        _con.push_back(x);
        ajust_up(_con.size() - 1);
    }
    void pop()
    {
        swap(_con[0], _con[_con.size() - 1]);
        _con.pop_back();
        ajust_down(0);
    }
    const T& top()
    {
        return _con[0];
    }
    size_t size()
    {
        return _con.size();
    }
    bool empty()
    {
        return _con.empty();
    }
    void ajust_up(size_t child)
    {
        Compare com;
        size_t parents = (child - 1) / 2;
        while (child > 0)
        {
            //if (_con[parents] < _con[child])
            if (com(_con[parents], _con[child]))
            {
                swap(_con[parents], _con[child]);
                child = parents;
                parents = (child - 1) / 2;
            }
            else
                break;
        }
    }

    void ajust_down(size_t parents)
    {
        Compare com;
        size_t child = parents * 2 + 1;
        while (child < _con.size())
        { 
            //if (child + 1 < _con.size() //考虑右孩子
            //	&& _con[child + 1] > _con[child])
            if (child + 1 < _con.size() //考虑右孩子
                && com(_con[child], _con[child + 1]))
            {
                ++child;
            }
            /*if (_con[child] > _con[parents])*/
            if (com(_con[parents], _con[child]))
            {
                swap(_con[child], _con[parents]);
                parents = child;
                child = parents * 2 + 1;
            }
            else break;
        }
    }

private:
    container _con;
};

leaf-view

关注

50
点赞
踩
41

收藏

觉得还不错? 一键收藏
2
评论
一文详解:堆、堆排序、topK问题及优先级队列

如果有一个关键码的集合K={k0, k1, k2, …, kn}，它这些关键码按照完全二叉树的顺序存储方式存储到一维数组中，且满足：父节点的值=子节点的值），则称为小顶堆（或者大顶堆）。int size;}HP;堆排序使用堆来选数，效率就高了很多。时间复杂度：建堆O(N) 排序O(N*logN)空间复杂度：O(1)不稳定。
复制链接

扫一扫