程序挑战设计

Peter_1125

于 2021-01-23 19:58:01 发布

阅读量150

点赞数

分类专栏： C++ 算法

本文链接：https://blog.csdn.net/Peter_1125/article/details/113060515

版权

C++ 同时被 2 个专栏收录

1 篇文章 0 订阅

订阅专栏

算法

1 篇文章 0 订阅

订阅专栏

写在前面：

本人编程能力菜鸡一个，就是记录下在学习这本书过程中学习到的一些新点子(不定期更新)，而且自己写的代码确实可读性也一般，所以大佬勿怪。如果我的记录过程恰巧能够为在学习这些的你提供一些小帮助或者启发，那我无比荣幸！也欢迎大家如果有相关问题讨论可以留言，不胜感激~(嗷对了俺用的是c++)

第一章基础篇

本章有两个题目我比较喜欢，可以通过技巧大幅度优化时间复杂度的。

1.ants题目

题目的大概意思是，n只蚂蚁以每秒1cm的速度在长为Lcm的竿子上爬行，当蚂蚁爬到端点时就会掉落。两只蚂蚁如果刚好相遇就只能反向爬回去。我们已知每只蚂蚁距离左端的距离xi，但不知道它们当前朝向。请计算所有蚂蚁落下竿子的最短时间和最长时间
输入：L=10，n=3，x={2，6，7}
输出：min=4(左、右、右)，max=8(右、右、右)

一般想法可能是穷举，一只蚂蚁两种朝向，n只蚂蚁有 $2^n$ 种可能，这个时间复杂度不大友好…所以我们分析一下这个问题。
最短时间的情况下，蚂蚁肯定是往自己朝向的方向去走，这种情况下不会产生碰撞情况。
最长时间的情况下，如果两只蚂蚁相遇，它们会朝反方向走，如果无视不同蚂蚁的区别那其实等价于两只蚂蚁相遇后保持原样交错而过。
在这里插入图片描述
如果无法理解就看这幅图，假设n在 $\frac{m+n}{2}$ 地方与m相遇，然后返回，总共走了距离是n+ $\frac{m-n}{2}$ *2=m，同理m也是如此，所以我们可以得知蚂蚁相遇后保持原样穿过也不会有问题，所以最长时间就只需要求出蚂蚁到竿子的最远距离即可。
代码如下：

#include <iostream>
using namespace std;

void Solve_1(int l,int n,int* x) //两只蚂蚁相遇后，可以看作还是原样前进，所以最长时间问题转化为求每只蚂蚁离两端距离，一起求最值
{
    int min_num=0;
    int max_num=0;
    for(int i=0;i<n;i++)
    {
        min_num=max(min_num,min(x[i],l-x[i])); //蚂蚁必须全部掉落才有效，所以要取所有蚂蚁中的最大值
    }
    for(int i=0;i<n;i++)
    {
        max_num=max(max_num,max(x[i],l-x[i]));
    }
    cout<<"min:"<<min_num<<","<<"max:"<<max_num<<endl;
}
int main()
{
    int l,n=0;
    cout<<"请输入杆子长度：\n";
    cin>>l;
    cout<<"请输入蚂蚁数量：\n";
    cin>>n;
    cout<<"请分别输入它们离杆子左端的距离：\n";
    int* x=new int[n];
    for(int i=0;i<n;i++)
    {
        cin>>x[i];
    }
    Solve_1(l,n,x);
    delete []x;
    return 0;
}

2.抽签题目

题目大致说，给出一堆带有数字的卡片，再选择一个数，抽一次然后放回，反复四次，问有没有可能让四次抽出卡片的和等于这个数
输入：n=3，m=10，nums={1，3，5} (一共三张卡片，凑出10，卡片分别是1、3、5)
输出：yes
如果四重循环，时间复杂度O( $n^4$ )实在是太大，所以我们尝试简化下

方法1 时间复杂度O( $n^3$ logn)

先查三次，最后一次数值为m-nums[a]-nums[b]-nums[c]，利用二分查找即可。

#include <iostream>
using namespace std;

bool isvaliable=0;
bool binary_search(int n,int d,int *nums)
{
    int left=0,right=n-1;
    while(right>left) 
    {
        int mid=(right+left)/2;
        if(d>nums[mid]) //如果这个数比中间的大，说明在后面
        {
            left=mid+1;
        }else if(d<nums[mid])//如果这个数比中间的小，说明在前面
        {
            right=mid;
        }else
        {
            return true;
        }
    }
    return false;
}
void solve_1(int n,int m,int *nums) //时间复杂度为O(n*n*n*logn)
{
    sort (nums, nums+n);
    bool f=false;
    int a,b,c,d;
    for(a=0;a<n;a++)
    {
        for(b=0;b<n;b++)
        {
            for(c=0;c<n;c++)
            {
                d=m-nums[a]-nums[b]-nums[c];
                if(binary_search(n,d,nums))
                {
                    f=true;
                    break;
                }
            }
            break;
        }
        break;
    }
    if(true)
    {
        cout<<"a="<<nums[a]<<",b="<<nums[b]<<",c="<<nums[c]<<",d="<<d<<endl;
    }else
    {
        cout<<"不存在这样的组合！\n";
    }
}

int main()
{
    int m,n=0;
    cout<<"请输入签数：\n";
    cin>>n;
    cout<<"请输入目标数：\n";
    cin>>m;
    int *nums=new int[n];
    cout<<"请输入这些签：\n";
    for(int i=0;i<n;i++)
    {
        cin>>nums[i];
    }
    solve_1(n,m,nums);
    delete []nums;
    return 0;
}

方法2 时间复杂度O( $n^2$ logn)

上一种方法只在最后一层考虑了二分查找，这次把最后两层设置为二分查找，需要一个辅助数组，依次对这个数组中元素两两求和存入辅助数组然后排序即可进行二分查找

#include <iostream>
using namespace std;

bool isvaliable=0;
bool binary_search(int n,int d,int *nums)
{
    int left=0,right=n-1;
    while(right>left) 
    {
        int mid=(right+left)/2;
        if(d>nums[mid]) //如果这个数比中间的大，说明在后面
        {
            left=mid+1;
        }else if(d<nums[mid])//如果这个数比中间的小，说明在前面
        {
            right=mid;
        }else
        {
            return true;
        }
    }
    return false;
}
void solve_2(int n,int m,int *nums) //时间复杂度为O(n*n*logn)
{
    //这种方法的主要思路是，把后两个数可能的和存储起来，然后对他们使用二分查找。也就是O(n*n)+O(n*n*logn)
    //为了满足题目需求，就不像方法1一样同时输出是哪些值了
    int *temp=new int[n*n];
    for(int c=0;c<n;c++)
    {
        for(int d=0;d<n;d++)
        {
            temp[c*n+d]=nums[c]+nums[d];
        }
    }
    sort(nums, nums+n);
    sort(temp,temp+n*n);
    bool f=false;
    for(int a=0;a<n;a++)
    {
        for(int b=0;b<n;b++)
        {
            int x=m-nums[a]-nums[b];
            if(binary_search(n,x,nums))
            {
                f=true;
                break;
            }
        }
        break;
    }
    if(true)
    {
        cout<<"这样的组合存在！\n";
    }else
    {
        cout<<"不存在这样的组合！\n";
    }
    delete []temp;
}

int main()
{
    int m,n=0;
    cout<<"请输入签数：\n";
    cin>>n;
    cout<<"请输入目标数：\n";
    cin>>m;
    int *nums=new int[n];
    cout<<"请输入这些签：\n";
    for(int i=0;i<n;i++)
    {
        cin>>nums[i];
    }
    solve_2(n,m,nums);
    delete []nums;
    return 0;
}

总体来看，这个问题的处理方法是分成两部分，一部分是直接遍历，一部分利用二分查找(有些情况可能需要构造新数组)，如果最初的那种四重循环，就是O( $n^4$ )+O(0)=O( $n^4$ )+O(0)；如果最后一层用二分查找，则为O( $n^3$ logn)+O(n)=O( $n^3$ logn)(理论上来说这个新数组需要排序，但题目中我们直接改动了原数组nums)；如果最后两层用二分查找，则为O( $n^2$ logn)+O( $n^2$ )=O( $n^2$ logn)，所以这就是为什么如果只用这思路O( $n^2$ logn)就是最小的时间复杂度了，因为如果再对三层做二分查找，那构造一个新数组用O( $n^3$ )就得不偿失了。

第二章基础篇

在“穷竭搜索”部分中，主要介绍了递归、深度优先搜索和广度优先搜索。例题的话选择两个，分别是dfs和bfs的。

1.Lake Counting

题目的大致意思是，一个N*M的园子，雨后积了水。八连通的积水被认为是连接在一起的。求出一个园子里一共有多少水洼？(八连通指的是下图中相对W的*部分)
* * *
* w*
* * *
例：如图，N=10，M=12，图中w表示积水，.表示没有积水，则输出结果为3
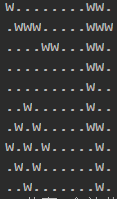
在这里插入图片描述
题中讲解的是八连通情况，不要被误导以为只有这样才算水洼。(所以之前好长时间都没读懂题，后来网上查了下题的意思才大概明白)，其实和实际情况很类似，想象一个布满了小坑洼的院子积满了水，我们统计有几片水洼的时候，不是要求每一块周围的八个方向坑洼里都是水，而是只需要整体在一起成一大摊就可以(也就是说大水洼里的小水洼可以共用某些坑洼来连通成大的)，如果中间断的实在连不上才分成整体的两滩。示例中的图案，明显的三块大水洼。

思路是dfs，我们选择一个有水的w开始，从八个方向依次遍历，找到下一个就把邻接的w用.代替，直到周围都没有w了，1次dfs结束。所以进行到图中没有w的时候，我们就可以知水洼的个数就是dfs一共进行的总次数。

#include <iostream> 
using namespace std;
//Lake Counting
int n,m;
char **field;


void dfs(int x,int y)
{
    field[x][y]='.';//先把自身置为.，这样不会在循环中重复
    for(int i=-1;i<=1;i++)//针对八个方位进行判断
    {
        for(int k=-1;k<=1;k++)
        {
            if(x+i>=0 && x+i<n && y+k>=0 && y+k<m && field[x+i][y+k]=='w')//是否在园子范围内而且为w 
            //注意这里因为都是对角标操作，所以应该是>=0和<边界M、N
            {
                dfs(x+i,y+k);
            }
        }
    }
    return;
}

int main()
{
    int res=0;
    cout<<"请输入园子的宽：\n";
    cin>>n;
    cout<<"请输入园子的长：\n";
    cin>>m;
    field= new char*[n]; //这句话不要放在前面，因为还没给n赋值，会报错
    for(int i=0;i<n;i++)
    {
        field[i]=new char[m+1];
    }
    cout<<"请逐行输入这个园子的样子：\n";
    for(int i=0;i<n;i++)
    {
        for(int k=0;k<m;k++)
        {
            cin>>field[i][k];
        }
    }

    for(int i=0;i<n;i++)
    {
        for(int k=0;k<m;k++)
        {
            if(field[i][k]=='w')//逐行遍历，找那些为w的
            {
                dfs(i,k);
                res++;
            }
        }
    }

    cout<<"一共有"<<res<<"个这样的水池"<<endl;

    for(int i=0;i<n;i++)
    {
        delete []field[i];
    }
    delete []field;
    return 0;
}

dfs很多情况下都借助递归实现，记得当时数据结构的老师上课的时候也提到过，递归一定要先明确出口，也就是结束条件，本题当中就是找不到w的时候停止。

2.迷宫的最短路径

给定一个大小谓N*M的迷宫，迷宫由通道和墙壁组成，每一步可以向邻接的上下左右方向的通道移动，一次只能移动一格，求出从起点到终点所需最小步数，假定起点一定可以到终点。

例：如图，N=10，M=10，迷宫中#代表墙壁，.代表通道，S代表起点，G代表终点，则输出结果为22。
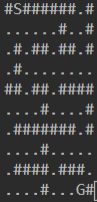
在这里插入图片描述
题意很好理解，那本题我们要用dfs还是bfs呢？因为两种方法都能遍历每一种状态，但是本题选用bfs会好一些，因为dfs做这种最短路径题，需要反复经过同样的状态(想象一下先是迷宫里一条路走到黑，发现不行还得退回来重新走)。
dfs一般借助递归实现，所以相当于使用了栈，bfs则是借助于队列来完成，走到一个地方就把四个方向能不能继续走存到队列去，然后先进先出进行尝试，撞墙了就直接再pop队列里的底部状态即可，不用回溯。
这个题因为是二维数组展示迷宫，所以压入队列的元素最好使用pair型，正好对应横纵坐标。
bfs中很重要的一个步骤就是标记哪些是自己已经访问过的状态，本题要求最短距离所以我们可以设置一个N*M的d数组来存放从起点到每个点的最短距离。初始化的时候用最大值INT_MAX即可，这样未到达的位置就是INT_MAX，明显标记出来了。一旦到达终点就停止，此时如果d中还有点是INT_MAX，说明这些点是不可达点。(这个设计比较巧妙)
此外还有一个是用dx[4]和dy[4]两个数组组合来表示四个方向向量，这样一个循环就可以实现四个方向移动的遍历，非常方便。

#include <iostream>
#include <queue>  //队列
#include <cmath> //最值
using namespace std;
//广度优先 迷宫问题

typedef pair<int,int> P;
int N,M;
int sx,sy; //起点坐标
int gx,gy; //终点坐标
char** maze;//存储迷宫图案
int** d;//存储到各个位置最短距离
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1}; //dx dy这样设计 刚好对应上下左右四个方向，一个for循环即可解决遍历四个方向问题

int bfs()
{
    queue<P> que; //P已经是一个typedef了，定义一个该类型的队列que
    for(int i=0;i<N;i++)//因为我们求最小距离，所以初始化这个存储最小距离的数组要全部置为最大值
    {
        for(int k=0;k<M;k++)
        {
            d[i][k]=INT_MAX;
        }
    }
    que.push(P(sx,sy));
    d[sx][sy]=0; //起点加入队列，这一点最小距离置为0

    while(que.size()) //不断循环直到队列长度为0
    {
        P a=que.front();
        que.pop();//取出队列底端的
        if(a.first == gx && a.second == gy)//如果取出终点，则直接跳出循环，结束
        {
            break;
        }

        for(int i=0;i<4;i++)
        {
            int nx=a.first+dx[i];
            int ny=a.second+dy[i];
            if(0<=nx && nx<N && 0<=ny && ny<M && maze[nx][ny]!='#' && d[nx][ny]==INT_MAX)//是否撞墙，是否为没有走过的地方
            //注意nx<N ny<M没有等号 否则会溢出错误 因为是下标
            {
                que.push(P(nx,ny));
                d[nx][ny]=d[a.first][a.second]+1;
            } 
        }
    }
    return d[gx][gy];
}

int main()
{
    cout<<"请输入迷宫的宽N：\n";
    cin>>N;
    cout<<"请输入迷宫的长M：\n";
    cin>>M;
    maze=new char* [N];
    d=new int* [N];
    for(int i=0;i<N;i++)
    {
        maze[i]=new char[M+1];
        d[i]=new int[M];
    }
    cout<<"请逐行输入这个迷宫的构造：\n";
    for(int i=0;i<N;i++)
    {
        for(int k=0;k<M;k++)
        {
            cin>>maze[i][k];
        }
    }
    for(int i=0;i<N;i++)//找起点终点坐标
    {
        for(int k=0;k<M;k++)
        {
            if(maze[i][k]=='S')
            {
                sx=i;
                sy=k;
            }else if(maze[i][k]=='G')
            {
                gx=i;
                gy=k;
            }
        }
    }

    int res=bfs();
    cout<<"最短距离为："<<res<<endl;
    

    for(int i=0;i<N;i++)
    {
        delete []maze[i];
        delete []d[i];
    }
    delete []maze;
    delete []d;
    return 0;
}

有一处是值得思考的，既然d存的是最短距离，那万一之前存了个距离，第二次这个点有更小距离了，但是代码中却只判断那些还未被标记的，这就不是最短距离了，所以对于d[nx][ny]的更新不借助最小值比较函数min(d[nx][ny],d[x][y]+1)，不太放心。其实仔细想想这种情况不可能发生，假设从一个点到另一个点有两条不同长短的通路，那肯定是短的那个先到这里。**也就是由于每次都只能移动一格，速度恒定，所以距离短就是到这个点用时短，也就是先到，所以无形中就产生了最短距离。**而用min函数来更新是有弊端的，如果INT_MAX=2³¹-1，还用min(d[nx][ny],d[x][y]+1)更新就有可能产生INF+1=-2³¹溢出的情况。但是本题没这个情况，所以这个题用了也没事~

Peter_1125

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
2
评论
程序挑战设计

写在前面：本人编程能力菜鸡一个，就是记录下在学习这本书过程中学习到的一些新点子(不定期更新)，而且自己写的代码确实可读性也一般，所以大佬勿怪。如果我的记录过程恰巧能够为在学习这些的你提供一些小帮助或者启发，那我无比荣幸！也欢迎大家如果有相关问题讨论可以留言，不胜感激~(嗷对了俺用的是c++)第一章基础篇本章有两个题目我比较喜欢，可以通过技巧大幅度优化时间复杂度的。1.ants题目题目的大概意思是，n只蚂蚁以每秒1cm的速度在长为Lcm的竿子上爬行，当蚂蚁爬到端点时就会掉落。两只蚂蚁如果刚好相遇就
复制链接

扫一扫