思考:站在程序的角度看,如何快速计算出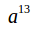
1. 第一种方法:写一个for循环,循环13次,每次让前一个值乘以a.即可得出结果.(计算12次)
2. 使用二进制幂算法 , 只需要5次计算过程
二进制幂的计算过程:
首先将13使用二进制表示:1101,然后建立表格,第二行的第一个值为a(不用计算),
后面的每个单元格计算方式:
- 如果所求单元格对应的二进制位为1,:那该单元格的值=前一单元格的值的平方*a
- 若所求单元格对应的二进制位为0,那么所求单元格的值=前一单元格的值的平方
程序伪代码:
LeftRightBinaryExponentiation(a,b(n))
//用从左到右二进制幂算法计算a^n
//输入:一个底数a和二进制位bi,...,b0的列表b(n),这些位来自于一个正整数n的二进制展开式
//下面的 <- 表示赋值过程
product <- a
for i <- (I-1) downto 0 do
product <- product * product
if b[i] = 1 product <- product * a
return product从伪代码看,二进制幂算法计算次数M(n)明显减少,
(b-1)<=M(n) <= 2(b-1),其中b代表二进制位的长度.考虑到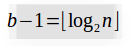























 1000
1000

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








