本文介绍了树的定义、基本术语，并重点探讨了二叉树和二叉查找树的概念。二叉查找树是一种特殊的二叉树，其中每个节点最多有两个子节点，且左子节点的值小于当前节点，右子节点的值大于当前节点。文章还详细讲解了二叉查找树的插入、遍历（中序、先序、后序）和查找操作，包括查找最大值和最小值的方法，以及如何在二叉查找树上删除节点。
树(tree)形结构是一种重要的非线性结构，依据分支关系定义的层次结构，在这种结构中，每个元素至多只有一个前趋，但可以有多个后继。
树的定义：树(Tree)是n(n 大于等于0)个节点的有限集合T，当n=0时称为空树，否则，称为非空树。
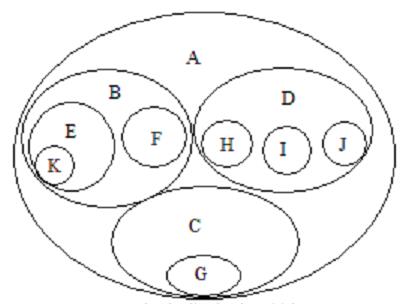
常用的树形表示方法有： 1。集合嵌套法2.凹入表表示法
3.广义表表示法
(A(B(E(k),F),C(G),D(H,I,J))
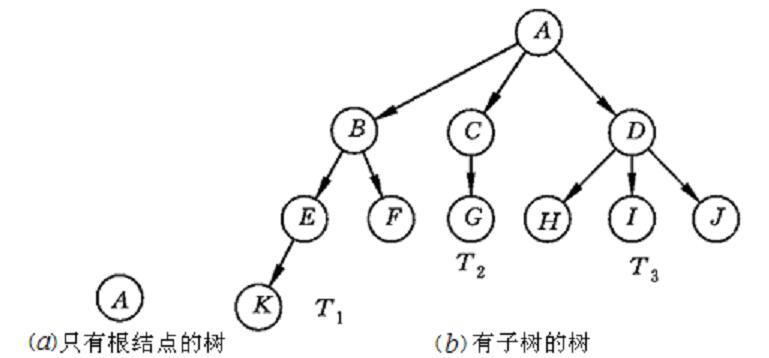
4.树形表示法 （最常见的表示法）
树的基本术语：
节点：就是指树中的元素
子节点： 树中一个节点的 直属下级节点
父节点： 当前节点的前趋节点
祖先节点：当前节点的前趋节点(非父节点)
子孙节点：当前结点的下属节点(非直接下属节点)
叶子节点：没有子节点的节点元素
节点的层次：根节点是第一层节点，表示节点的所属的层数
深度：树的层数，表示树的深度
森林： n棵互不相交的树的集合
最低0.47元/天 解锁文章
扫一扫
3055
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
