Is It A Tree?
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 32211 | Accepted: 10925 |
Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
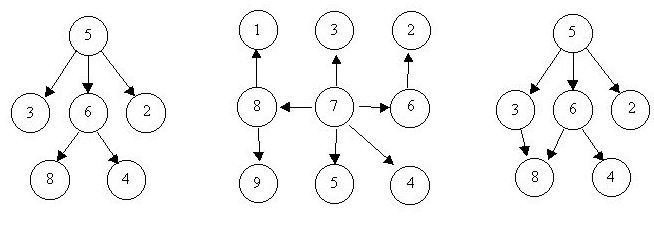
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.

In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1
Sample Output
Case 1 is a tree. Case 2 is a tree. Case 3 is not a tree.
看似水题,实则很坑
例如:0 0是一棵空树,是树
1 2 2 1 0 0 不是树
1 2 4 5 0 0 是森林,不是树。
一开始,我用计算每个节点的入度,并判断是否有多于1个节点入度为0和是否没有节点入度为0来判断
结果这组数据1 2 2 1 4 5 0 0,错
贴上WA的代码:
//By Sean Chen
#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#include <queue>
using namespace std;
map <int,int> indegree;
queue <int> occurence;
map <int,int> visit;
int st,ed,Case,flag,rootexist;
int main()
{
while (1)
{
scanf("%d%d",&st,&ed);
if (st==-1 && ed==-1)
break;
if (st==0 && ed==0)
{
flag=0;
rootexist=0;
int temp;
while (occurence.size())
{
temp=occurence.front();
occurence.pop();
if (indegree[temp]>1)
flag=1;
if (indegree[temp]==0)
{
if (rootexist)
flag=1;
else
rootexist=1;
}
}
indegree.clear();
visit.clear();
if (flag)
printf("Case %d is not a tree.\n",++Case);
else
printf("Case %d is a tree.\n",++Case);
}
else
{
indegree[ed]++;
if (visit[st]==0)
{
occurence.push(st);
visit[st]=1;
}
if (visit[ed]==0)
{
occurence.push(ed);
visit[ed]=1;
}
}
}
return 0;
}
然后改用并查集实现,成功AK
代码:
//By Sean Chen
#include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
using namespace std;
int num=1;
set <int> s;
int root[100100];
int flag;
void init()
{
for(int i=1;i<100100;i++)
root[i]=i;
flag=0;
s.clear();
}
int findroot(int x)
{
if (x==root[x])
return x;
return findroot(root[x]);
}
int main()
{
int x,y;
init();
while(1)
{
scanf("%d%d",&x,&y);
if (x==-1 && y==-1)
break;
if(x==0&&y==0)
{
if(flag==0)
{
int cnt=0;
for(set<int>::iterator it=s.begin();it!=s.end();it++)
{
if(root[*it]==*it) cnt++;
}
if(cnt>1) flag=1;
}
if(flag)
printf("Case %d is not a tree.\n",num++);
else
printf("Case %d is a tree.\n",num++);
init();
continue;
}
else if(!flag)
{
s.insert(x);
s.insert(y);
int rootx=findroot(x);
int rooty=findroot(y);
if(rootx==rooty)
flag=1;
else if(y!=findroot(y))
flag=1;
else
root[rooty]=rootx;
}
}
return 0;
}























 775
775

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








