硅基计划4.0 算法 双指针

一、移动零
题目链接
这道题,我们利用的就是快排思维,我们利用双指针,可以把一个数组划分成三个区域

利用这个特性,我们可以这样子,我们定义两个指针,右指针负责遍历数组,左指针负责指定处理位置,我们让左指针从-1开始,避免和右指针抢位置
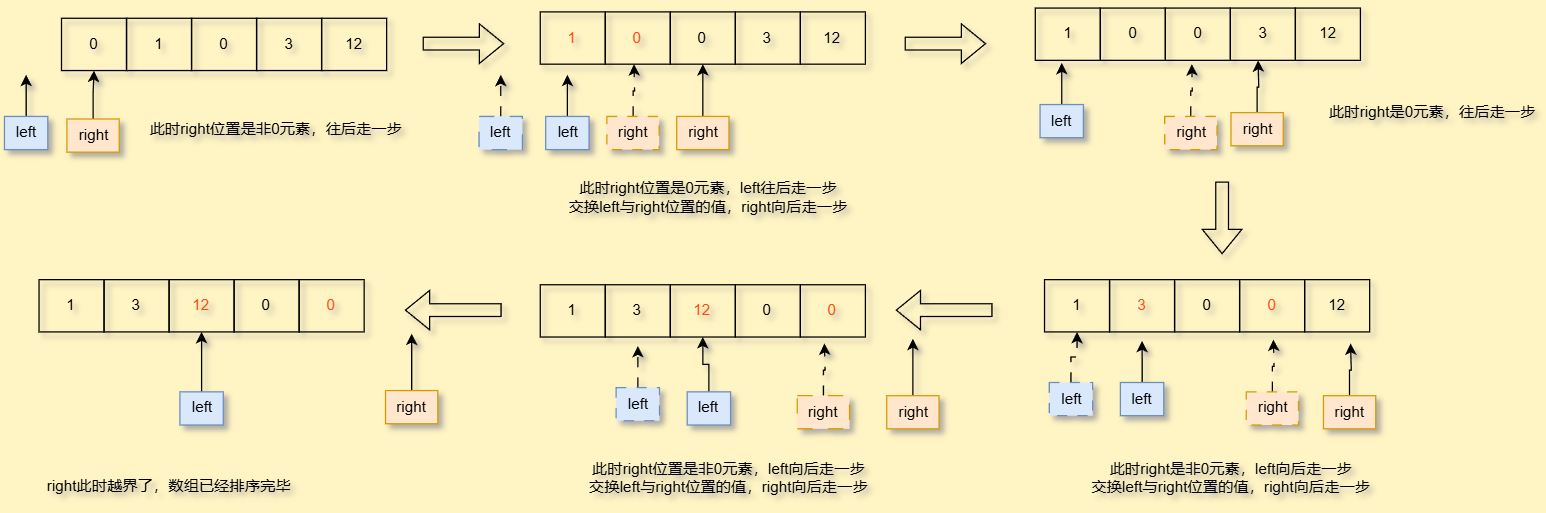
- 当我们的右指针遇到0元素的时候,因为题目要求0元素在右边,因此我们不用处理
- 当我们的右指针遇到非0元素时候,我们的左指针往后走一步,交换我们的数据,交换完毕后,右指针继续往后走遍历数组
class Solution {
public void moveZeroes(int[] nums) {
int left = -1;
for(int right = 0;right < nums.length;right++){
if(nums[right] != 0){
left++;
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
}
}
二、复写零
题目链接
这道题的核心还是利用双指针的错位性去解决问题,这道题意思就是碰到0元素我们需要重复两次
我们尝试按照刚刚那一题的逻辑

此时你会发现我们从前往后,会把原来的值覆盖,因此我们尝试从后往前,我们先按照自己的主观判断,我们看到示例中输出的最后一个数是4,因此我们知道原数组中最后一个覆写的数就是4
因此我们可以定义左指针的位置是指向数字4的下标,右指针在数组末尾
- 左指针是非0的数,我们右指针就把左指针的值复制一份,此时我们左右指针同时左移就好
- 左指针是为0的数,我们右指针需要把左指针的值复制两份,此时我们左指针往左走了一步,右指针往左走了两步
就这样一直重复,最后我们两个指针都会同时到达数组开头的左边位置,此时我们循环结束

好,那目前的问题就是我们要如何寻找最后一个被覆写的数呢?
答案就是,噔!双指针算法,没错,我们前提需要再使用双指针算法
⚠️:此方法并非本人原创 ⚠️:此方法并非本人原创 ⚠️:此方法并非本人原创
我们按照上一题移动0的思路,定义两个指针,左指针起始位置是-1,右指针其实位置是0下标
- 当右指针遇到0元素,左指针就往后走两次,否则走一次
- 走完后判断左指针是否到了数组末尾,没有到则右指针再向后走一步,否则不要动
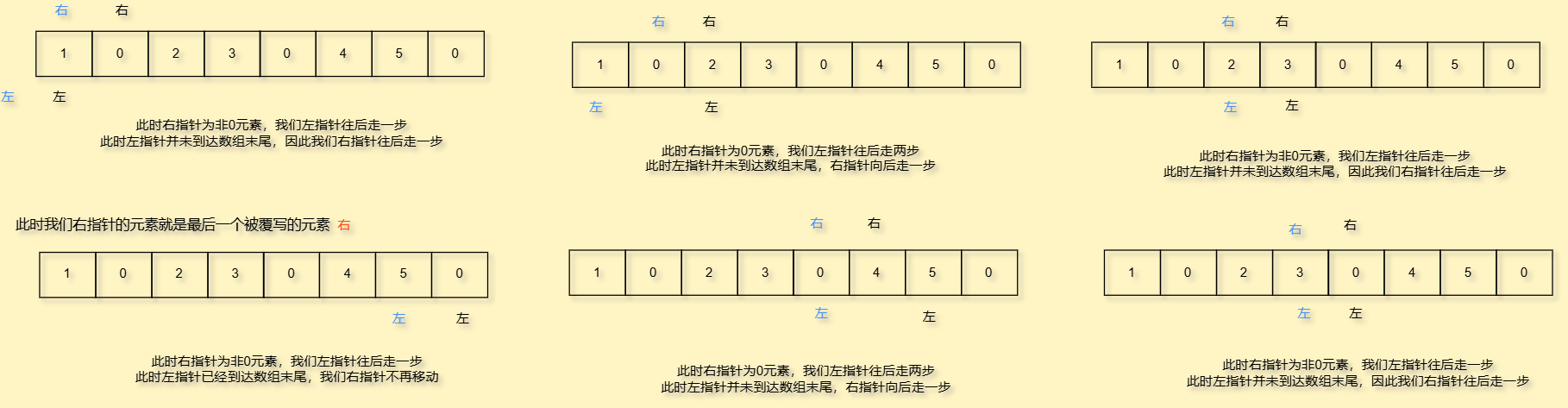
但是你以为此时就没有问题了吗,有一种特殊情况,就是你的倒数第二个数字是0,会导致左指针移动两次,导致越界

因此我们还要额外判断这种情况,因此这种情况我们要让左指针回到数组最后一个位置
经过上述的寻找最后一个被覆写的数,你也会发现,此时左右指针的位置不就恰好是我们从后往前覆写数组的左右指针的位置吗,此时我们直接循环开始往前覆写
class Solution {
public void duplicateZeros(int[] arr) {
int left = -1;
int right = 0;
//到达末尾或者是越界
while(left < arr.length){
if(arr[right] == 0){
left +=2;
}else{
left ++;
}
if(left >= arr.length-1){
break;
}
right++;
}
//处理边界
if(left == arr.length){
arr[arr.length-1] = 0;
left -= 2;
right--;
}
//覆写
while(left >= 0){
if(arr[right] == 0){
arr[left] = arr[right];
left--;
arr[left] = arr[right];
left--;
right--;
}else{
arr[left] = arr[right];
left--;
right--;
}
}
}
}
三、快乐数
题目链接
还记得我们之前学数据结构中的判断链表是否有环的问题吗,我们是利用快慢指针然后判断相遇来看是否有环
但是这和我们这一题有什么关系呢?其实有很大的关系,比如题目中示例的19这个数,变成1之后开始无限循环
19
=
1
2
+
9
2
=
82
,
82
=
8
2
+
2
2
=
68
,
68
=
6
2
+
8
2
=
100
,
100
=
1
2
+
0
2
+
0
2
=
1
,
1
=
1
2
=
1...
19=1^2+9^2=82,82=8^2+2^2=68,68=6^2+8^2=100,100=1^2+0^2+0^2=1,1=1^2=1...
19=12+92=82,82=82+22=68,68=62+82=100,100=12+02+02=1,1=12=1...
再比如2这个数
2
=
2
2
=
4
,
4
=
4
2
=
16
,
16
=
1
2
+
6
2
=
37
,
37
=
3
2
+
7
2
=
58
,
58
=
5
2
+
8
2
=
89
,
89
=
8
2
+
9
2
=
145
,
145
=
1
2
+
4
2
+
5
2
=
42
,
42
=
4
2
+
2
2
=
20
,
20
=
2
2
+
0
2
=
4......
2=2^2=4,4=4^2=16,16=1^2+6^2=37,37=3^2+7^2=58,58=5^2+8^2=89,89=8^2+9^2=145,145=1^2+4^2+5^2=42,42=4^2+2^2=20,20=2^2+0^2=4......
2=22=4,4=42=16,16=12+62=37,37=32+72=58,58=52+82=89,89=82+92=145,145=12+42+52=42,42=42+22=20,20=22+02=4......
此时我们发现经过一些列变换后又回来了
因此想要判断一个数是否环中存在数字1,仅需定义快慢指针,判断它们的相遇地方(也就是环的起点)是不是数字1就好
但是聪明的你肯定会问,难道一个数经过很多次变换就一定有环吗,我直接说结论,还真的是一定有,我们利用鸽巢原理来叙述
我们假设定义一个很大的数,比如999999999,我们求它各个位数的平方和,得出这个结果:729,诶,比这个数要小很多,我们再求729各个位数的平方和:134,更小了
因此我们就知道了,任何一个数,经过很多次变换后即使非常大,也会有一个顶点,然后开始数值减小,慢慢回落
感兴趣的可以去搜搜鸽巢原理的讲解视频哦!
class Solution {
public boolean isHappy(int n) {
int slow = n;
//保证进入循环,如果定义成n会导致无法进入循环
int fast = powNum(n);
while(slow != fast){
slow = powNum(slow);
fast = powNum(powNum(fast));
}
return fast == 1;
}
private int powNum(int n){
int sum = 0;
while(n != 0){
int pow = n % 10;
sum += pow*pow;
n /= 10;
}
return sum;
}
}
四、盛最多水的容器
题目链接
这道题意思就是寻找数组中的两个下标位置的元素,然后比较它们两个的最小值,得出最小值后再乘上两个下标的差值,即是“容器”的容积
这道题其实我们可以利用单调性原理想想
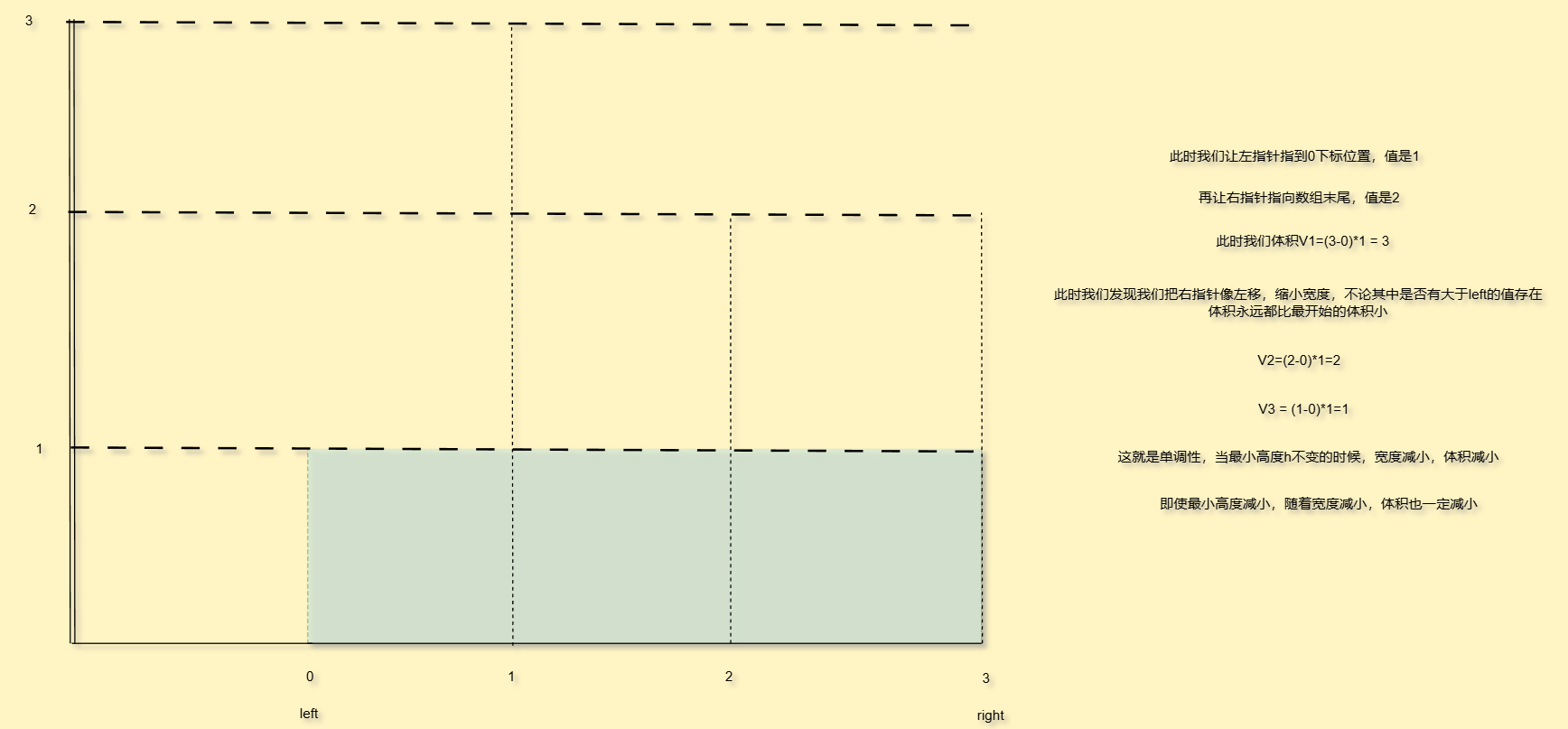
因此我们定义两个指针,一个在数组开头,一个在数组末尾
我们定义一个变量表示最小值,如果左右指针中间区域的最大体积比这个变量中的体积大,我们就更新体积最大值,否则两个指针都向内靠拢
我们具体来演示一下

class Solution {
public int maxArea(int[] height) {
int slow = 0;
int fast = height.length-1;
int max = 0;
while(slow < fast){
int v = (fast-slow)*Math.min(height[slow],height[fast]);
max = Math.max(max,v);
//height[slow] >= height[fast] ? fast-- : slow++;这么写不可以,C++可以
if(height[slow] >= height[fast]){
fast--;
}else{
slow++;
}
}
return max;
}
}
整体时间复杂度是O( n 2 n^2 n2)
五、排序+快慢指针
1. 有效三角形个数
题目链接
这道题意思就是从数组中找三个数构成三角形
比如[2,2,3,4]这个数组,我们可以找到[2,2,3],[2,3,4],[2,3,4],注意题目中说可以有重复数字
刚刚的三个结果中,[2,3,4],[2,3,4]中的两个2其实并不是同一个2
那我们如何去寻找呢,如果使用暴力算法三层循环,时间复杂度太高,不妥
那我们可以这样子,我们可以对数组进行排序,利用单调性去解决问题,比如
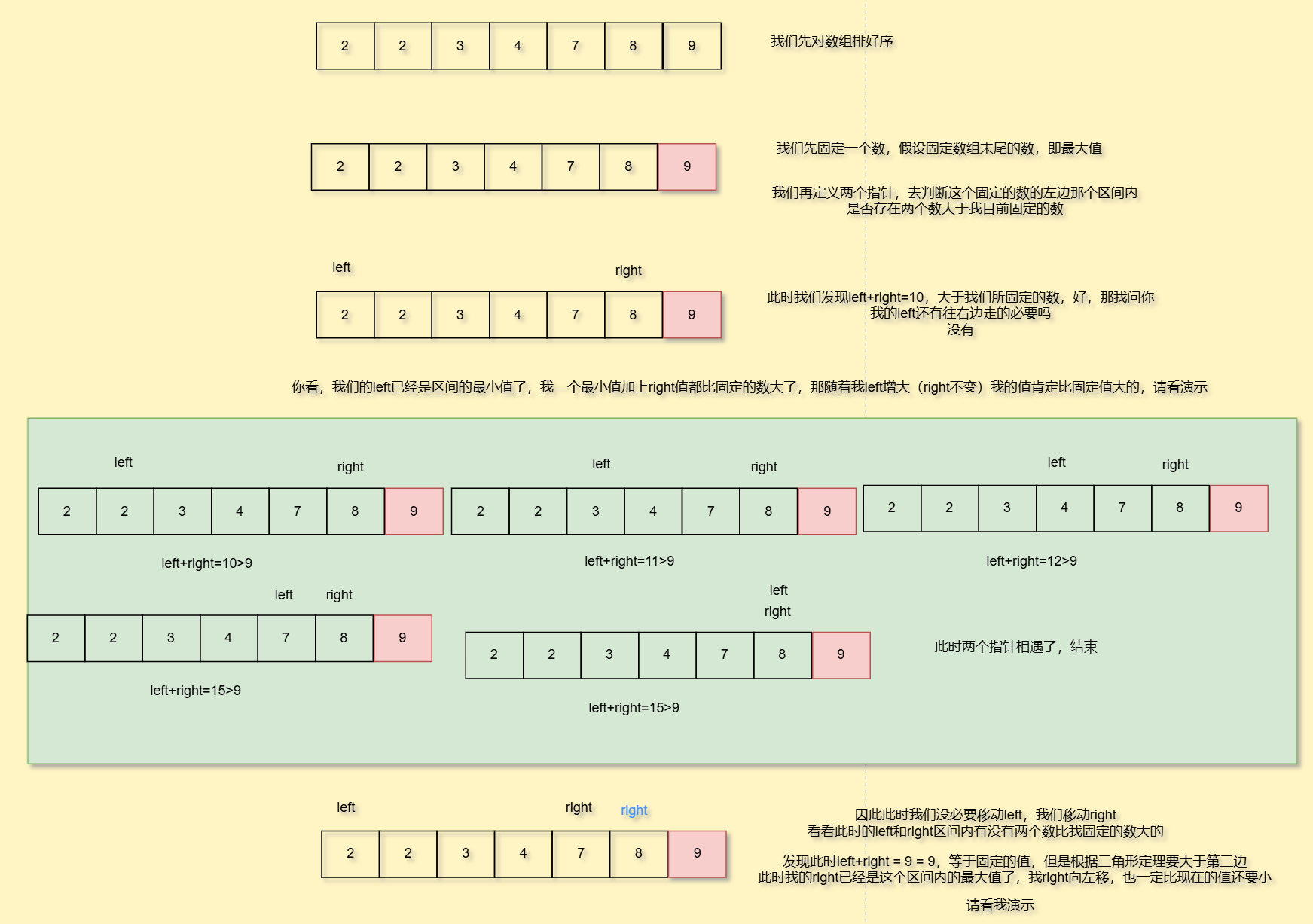
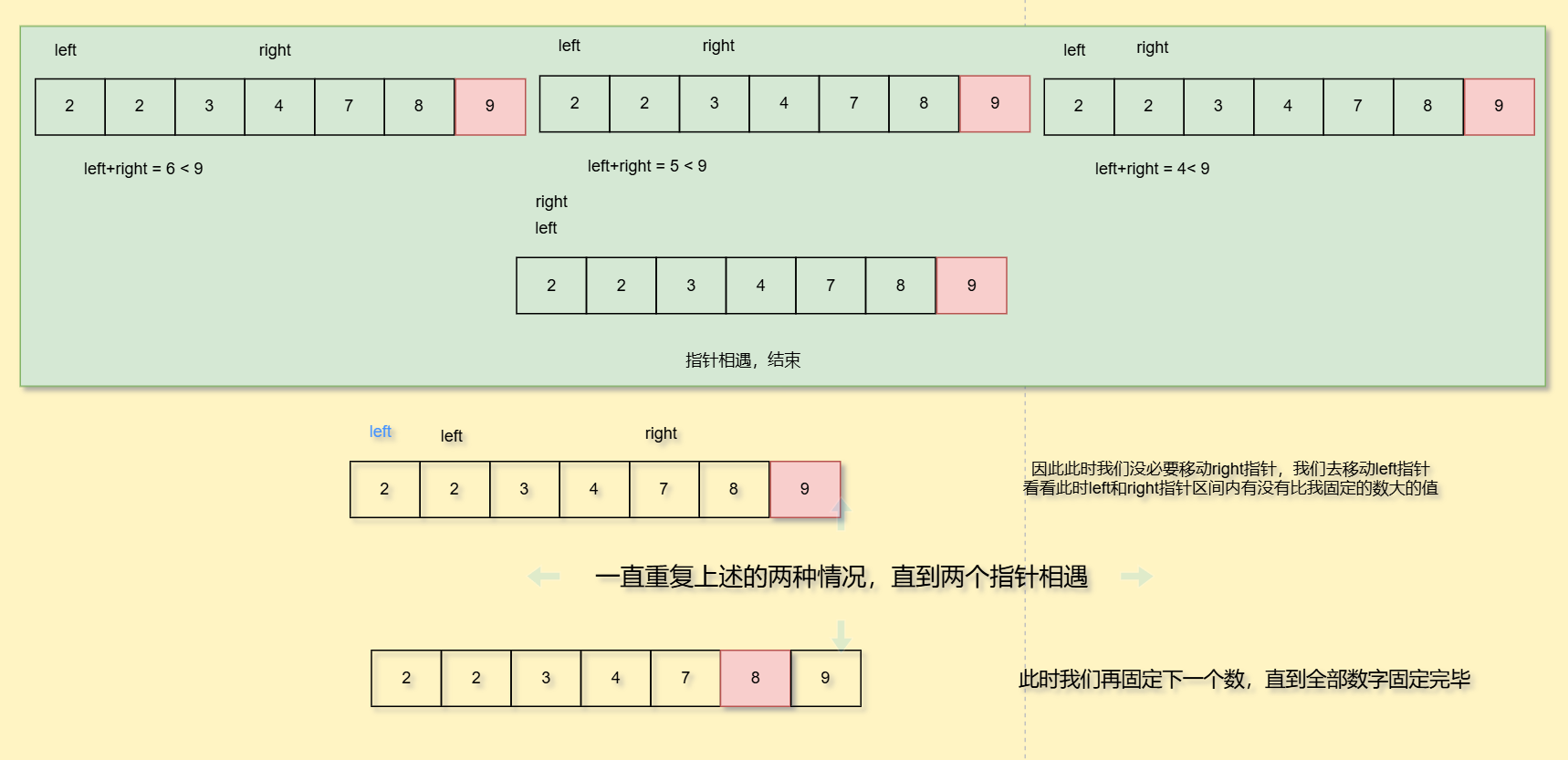
还要注意,测试用例的数组存在数组元素个数小于3的情况,也记得要判断一下哦
class Solution {
public int triangleNumber(int[] nums) {
if(nums.length <=2){
return 0;
}
Arrays.sort(nums);
int count = 0;
for(int i = nums.length-1;i>1;i--){
int left = 0;
int right = i-1;
while(left < right){
if(nums[left]+nums[right] > nums[i]){
count += right-left;
right--;
}else{
left++;
}
}
}
return count;
}
}
整体时间复杂度是O( n 2 n^2 n2)
2. 查找总价格为目标值的两个商品
题目链接
这题和刚刚那一题一模一样,还简单些,我们不需要固定第三个数了,我们直接去寻找是否有两个数和题目给的目标数相等就好了,连排序都省了
只不过返回值要注意下,返回数组是new int[]{数组元素},若找不到可以返回null或者是new int[]{0}
class Solution {
public int[] twoSum(int[] price, int target) {
int left = 0;
int right = price.length-1;
while(left < right){
int sum = price[left] + price[right];
if(sum < target){
left++;
}else if(sum > target){
right--;
}else{
return new int[]{price[left],price[right]};
}
}
return null;
}
}
3. 三数之和
题目链接
这道题有个特别的要求,要保证三个数不重复,什么意思,比如-1,0,1三个数组成的任意一种排序,都可以视为相同的结果
题目中还说,如果不存在符合要求的三个数返回0,存在几个符合要求的三个数就返回几个
看到这道题马上想到的就是暴力三循环枚举,把所有结果添加到容器中,然后去重返回结果,但是这样时间复杂度非常高
那有没有好的方法呢?有的,还记得我们上一题的排序双指针解法吗
⚠️:此方法并非本人原创 ⚠️:此方法并非本人原创 ⚠️:此方法并非本人原创
诶,我们可以先固定一个数,然后寻找另外两个数,让它们的和为固定的数的负数,进而三个数相加就是0了
但是题目要求我们不能有重复的情况,但问题是,怎么去重呢?
而且不光要去重,还要求我们不能漏掉每一种可能的组合,这就有点伤脑筋了
我们先处理不漏掉的情况,当我们找到一对符合要求的数后,我们不能直接终止循环,我们还要继续寻找

再看我们如何去重
我们假如判断了一对数符合要求后,我们两个指针移动的时候发现新的数和上一次的数一模一样,那其实我们根本不需要去比较了
因为结果会和上一次一样,请看我演示

但此时,就完了吗,并不是,我们固定的数也要考虑去重哦
你看,跟刚刚逻辑一样,如果我所固定的数是重复的,那我的结果必然也是重复的
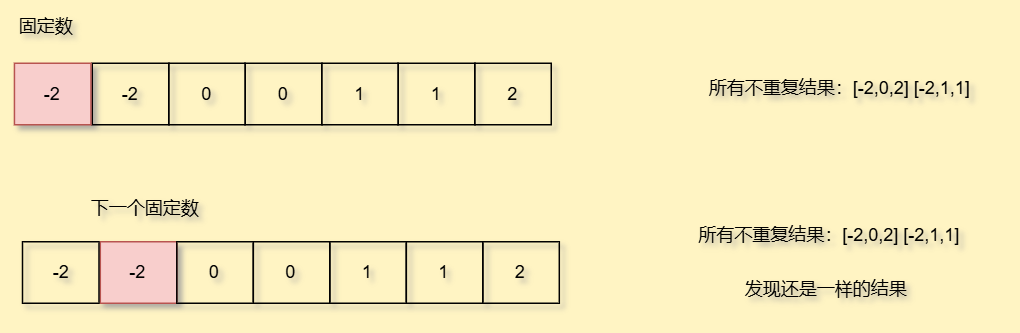
还有,如果我的固定数大于0,我在其右边寻找两个数,肯定是找不到符合要求的两个数
因为此时右边的数都是大于0的数,三个数和不可能出现负数的
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
int i = 0;
while(i < nums.length){
int left = i+1;
int right = nums.length-1;
int findNum = -nums[i];
while(left < right){
int sum = nums[left] + nums[right];
if(sum < findNum){
left++;
}else if(sum > findNum){
right--;
}else{
list.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[left],nums[right])));
left++;
right--;
while(left < right && nums[left] == nums[left-1]){
left++;
}
while(left < right && nums[right] == nums[right+1]){
right--;
}
}
}
i++;
while(i < nums.length && nums[i] == nums[i-1]){
i++;
}
}
return list;
}
}
4. 四数之和
题目链接
这题和刚刚一模一样,我们只需要固定一个数后,再剩下的三个数所构成的子区间内中再固定一个数
再在剩下的两个是定义双指针,在其子区间内寻找符合要求的数,和上述几题的要求一样
而且这一题要去重三次:双指针去重+第一次固定的数去重+第二次固定的数去重
还有注意,题目测试用例的数组中会出现很大的值的情况,我们要使用long类型去接收,去计算
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> list = new ArrayList<>();
int i = 0;
int length = nums.length;
while(i < length){
//第一层循环的目标值
int j = i+1;
while(j < length){
//第二层循环的目标值
//定义双指针遍历子区间
int left = j+1;
int right = length-1;
//使用long应对数据很大的情况[1000000000,1000000000,1000000000,1000000000]
//我只想问这是人能想的出来的数据
long targets = (long)target-nums[i]-nums[j];
while(left < right){
int sum = nums[left] + nums[right];
if(sum < targets){
left++;
}else if(sum > targets){
right--;
}else{
list.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
left++;
right--;
//双指针去重
while(left < right && nums[left] == nums[left-1]){
left++;
}
while(left < right && nums[right] == nums[right+1]){
right--;
}
}
}
//第二层循环目标值去重
j++;
while(j < length && nums[j] == nums[j-1]){
j++;
}
}
//第一层循环目标值去重
i++;
while(i < length && nums[i] == nums[i-1]){
i++;
}
}
return list;
}
}























 1165
1165

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








