BZOJ 1027 JSOI2007 合金 计算几何+Floyd

题目大意：给定一些合金，选择最少的合金，使这些合金可以按比例合成要求的合金

首先这题的想法特别奇妙 看这题干怎么会想到计算几何 而且计算几何又怎么会跟Floyd挂边 好强大

首先由于a+b+c=1 所以我们只要得到a和b即可 c=1-a-b 所以c可以不读入了

然后我们把每种原料抽象成一个点 可知两个点能合成的合金一定在两点连线的线段上

证明：设两个点为(x1,y1)和(x2,y2)，新合成的合金为(ax1+bx2,ay2+by2) (a+b=1,a,b>0) 两点连线为(y-y1)/(x-x1)=(y-y2)/(x-x2)，代入即可得证

那么我们选定一些原料，这些原料能合成的合金一定在这些点所在的凸包上 证明略

于是我们就把问题转化成了这样：给定两个点集A和B，求A中最小的一个子集S，使B中所有的点在S的凸包内部

这个问题怎么处理呢？这里用到一个十分巧妙的方法

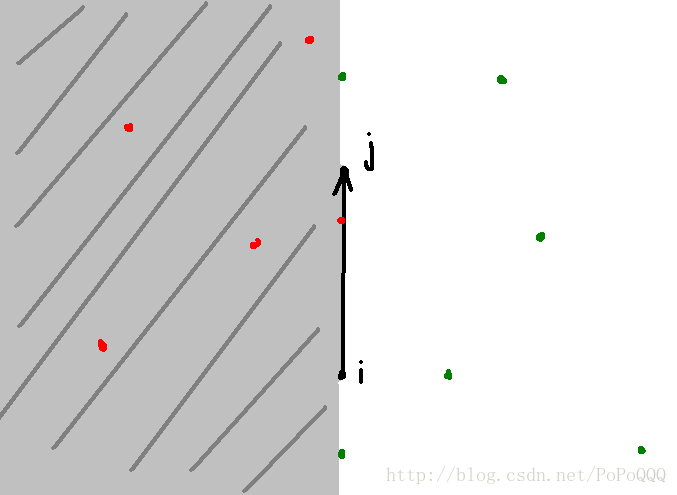
如图，枚举A点集两点i,j(i可以等于j)若B点集中的所有点都在向量i->j的左侧或线段ij上(图中红色的点)而没有点在图中绿色的点所在位置，就连接一条i->j的单向边

即 若任意B点集中的点k满足(k->i)×(k->j)<0||(k->i)×(k->j)==0&&(k->i)·(k->j)<=0 则连接一条i->j的单向边

然后Floyd求最小环即可

正确性自己YY吧 这样写应该是可以减少很多讨论并且不会被卡掉的 顺便吐槽一句数据实在太弱……

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define M 510
#define INF 0x3f3f3f3f
#define EPS 1e-7
using namespace std;
struct point{
	double x,y;
	point operator - (const point z)
	{
		point re;
		re.x=x-z.x;
		re.y=y-z.y;
		return re;
	}
	double operator * (const point z)
	{
		return x*z.y-y*z.x;
	}
	double operator ^ (const point z)//大家好我是萌萌哒的点积 乘号被叉积抢了主人只能给我这个了~ 
	{
		return x*z.x+y*z.y;
	}
}a[M],b[M];
int m,n;
int map[M][M],f[M][M];
int ans=INF;
void Floyd()
{
	int i,j,k;
	memcpy(f,map,sizeof f);
	for(k=1;k<=m;k++)
		for(i=1;i<=m;i++)
			if(f[i][k]<INF)
				for(j=1;j<=m;j++)
					f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
	for(i=1;i<=m;i++)
		ans=min(ans,f[i][i]);
}
int main()
{
	int i,j,k;
	memset(map,0x3f,sizeof map);
	cin>>m>>n;
	for(i=1;i<=m;i++)
		scanf("%lf%lf%*lf",&a[i].x,&a[i].y);
	for(i=1;i<=n;i++)
		scanf("%lf%lf%*lf",&b[i].x,&b[i].y);
	for(i=1;i<=m;i++)
		for(j=1;j<=m;j++)
		{
			for(k=1;k<=n;k++)
			{
				double cross=(a[i]-b[k])*(a[j]-b[k]);
				if( cross>EPS )
					break;
				if( fabs(cross)<EPS && (a[i]-b[k]^a[j]-b[k])>EPS )
					break;
			}
			if(k==n+1)
				map[i][j]=1;
		}
	Floyd();
	if(ans==INF)
		ans=-1;
	cout<<ans<<endl;
}