C++ 快速幂模板

最新推荐文章于 2024-07-18 08:41:54 发布

南瓜桐

最新推荐文章于 2024-07-18 08:41:54 发布

阅读量1.2k

点赞数 6

CC 4.0 BY-SA版权

文章标签： c++

本文链接：https://blog.csdn.net/Pumpkin_Tung/article/details/121443351

本文介绍了C++中解决大数快速幂运算的方法，通过分解指数为偶数和奇数的情况，减少计算次数，避免溢出问题。文章详细讲解了优化过程，包括每次计算后取模和使用位运算提升效率。

注：这是本蒟蒻的第一篇博客，语言表述方面可能有些欠缺，但我自认为还讲的挺清楚的

让我们开始吧！

我们常常遇到这样的问题：

给你三个数a,b,p

求 $a^{b}$ mod p = ?

首先很多人会想到用<cmath>库里的pow函数来求解：

于是就有了下面这段代码

#include<cstdio>
#include<iostream>
#include<cmath> 
using namespace std;
long long a,b,p;
int main(){
	scanf("%ld%ld%ld",&a,&b,&p);
	long long ans = pow(a,b);
	ans%=p;
	printf("%ld",ans);
	return 0;
}

值得注意的是因为pow返回的是浮点数，所以不能直接取模，向下面这样就会报错：

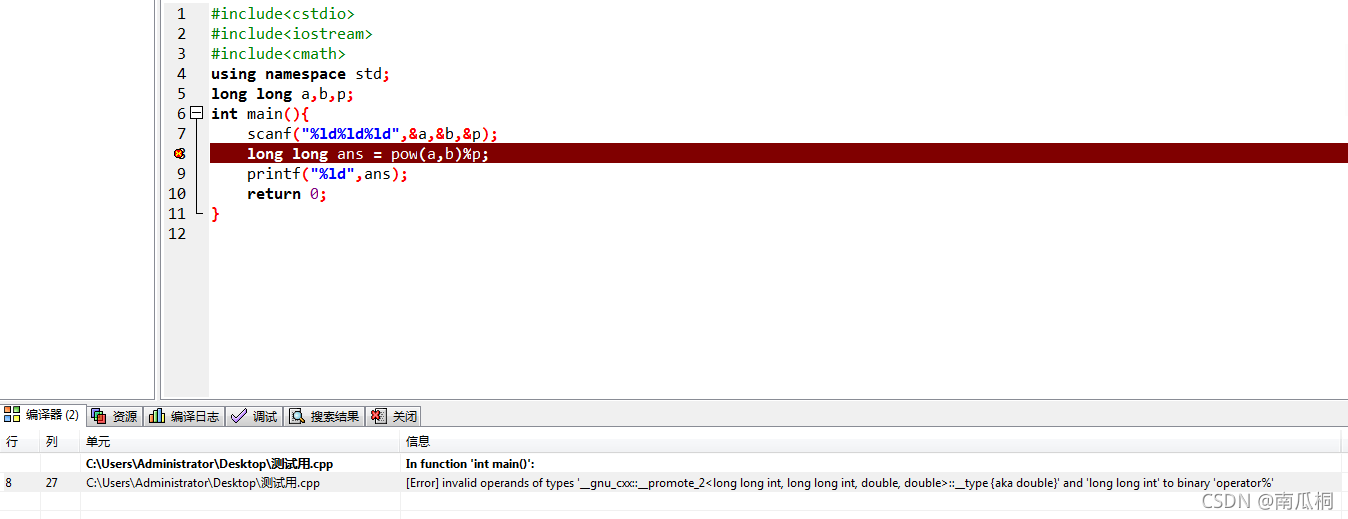
而浮点数被复值到ans后自动转化成整数，所以换一行取模即可

这就结束了？

答案是没有

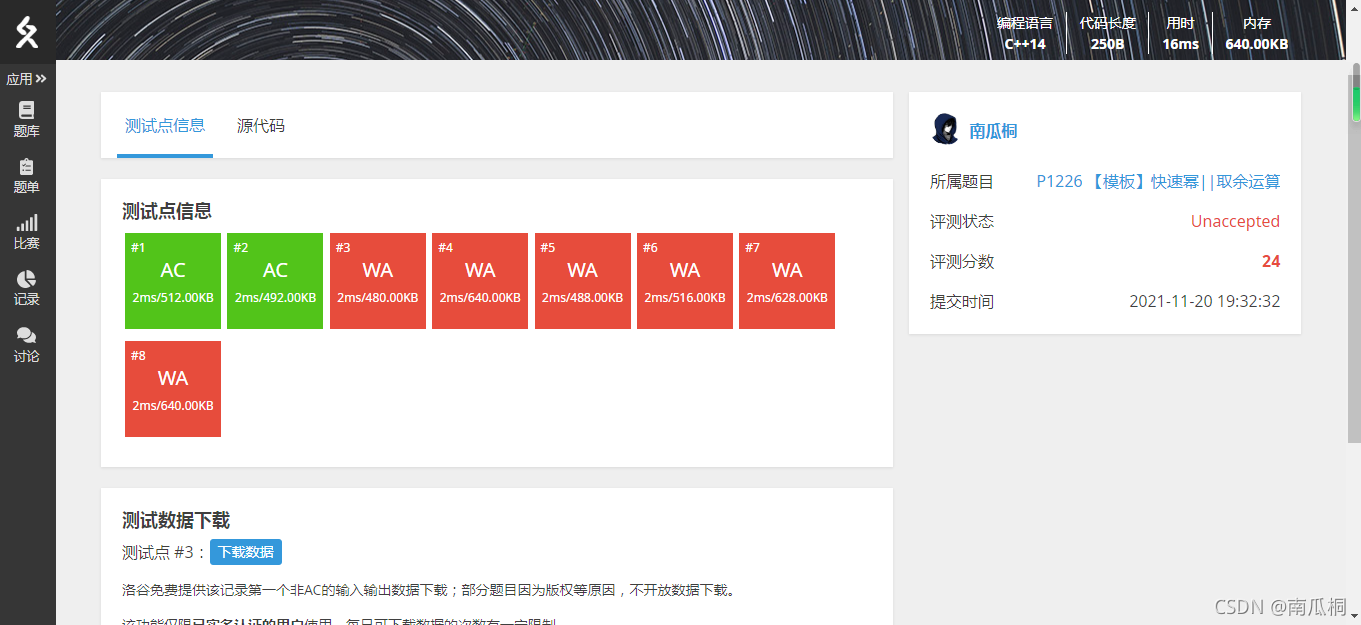
由上图可见，即使开了long long ， $a^{b}$ 这个是数还是太大了，在pow计算的过程中很容易溢出而导致结果错误。

如果我们算一次就取一次摸，是不是就不会溢出了？

因为同余定理（如果a mod p=0,b mod p=0,那么(a+b) mod p = 0）的存在，算一次就取一次摸不会影响答案的正确性

代码奉上

#include<cstdio>
#include<iostream>
#include<cmath> 
using namespace std;
long lon

最低0.47元/天解锁文章

200万优质内容无限畅学