本周进行了多方面的学习,进一步了解了ctf的知识,同时对密码学的同余知识、文件操作、Web前端也有了巩固的认知。
在同余中知道了Euler定理,想必这也是日后比较重要的算法基础;在文件操作中,首次进入到linux环境的学习中,不论是下载软件还是配置相应的环境也要我的能力提高,当然了也知道了一些工具的使用方法,这样能快突破。当然在一些ctf比赛中,Web前端还是必不可少,这样能做好很好的审计工作。
接下来一周还是比较忙的,不仅要撰写大创还要准备一下软件杯的相关事宜,总的时间不多,但还是要多学一些,主要还是以这三个模块进行深入学习!
以下是相应的学习内容!
密码学同余
1.同余式:
a
≡
b
(
m
o
d
m
)
a\equiv b(mod \ \ m)
a≡b(mod m)
m属于正整数,m|(a-b),存在k属于整数,使得a-b=km
2.a对模m的最小同余式分类
| 最小非负剩余 | 0<=b<m |
|---|---|
| 最小正剩余 | 1<=b<=m |
| 最小绝对剩余 | -m/2 <b<=m/2 |
- a ≡ b ( m o d m ) ⇔ { a = q 1 m + r 1 b = q 2 m + r 2 r 1 = r 2 a\equiv b(mod \ \ m)\Leftrightarrow \begin{cases} a=q_1m+r_1\\ b=q_2m+r_2 & {r1=r2} \end{cases} a≡b(mod m)⇔{a=q1m+r1b=q2m+r2r1=r2
整个证明不复杂,直接将两式相减可以得出m |(r1-r2),因为a-b=km,所以易得出r1=r2.
4.同余的关系:(等价关系)
自反性、对称性、传递性
同时也满足相乘性:
a
≡
b
(
m
o
d
m
)
c
≡
d
(
m
o
d
m
)
⇒
a
c
≡
b
d
(
m
o
d
m
)
a\equiv b(mod \ \ m) \ \ \ c\equiv d(mod \ \ m) \ \ \ \ \Rightarrow ac\equiv bd(mod \ \ m)
a≡b(mod m) c≡d(mod m) ⇒ac≡bd(mod m)
上面几个性质也都是显然可以得出
5.函数的同余性
f
(
x
)
=
a
n
x
n
+
.
.
.
+
a
0
f(x)=a_nx^{n}+...+a_0
f(x)=anxn+...+a0
g
(
x
)
=
b
n
x
n
+
.
.
.
+
b
0
g(x)=b_nx^{n}+...+b_0
g(x)=bnxn+...+b0
满足
a
j
=
b
j
(
m
o
d
m
)
o
≤
j
≤
n
a_j=b_j(mod \ \ m) \ \ o \le j \le n
aj=bj(mod m) o≤j≤n
则
f
(
x
)
≡
g
(
x
)
(
m
o
d
m
)
f(x) \equiv g(x) (mod \ \ m)
f(x)≡g(x)(mod m)
6.恒等式
a
c
≡
b
c
(
m
o
d
m
)
⇔
a
≡
b
(
m
o
d
m
(
c
,
m
)
)
ac \equiv bc(mod \ \ m) \ \Leftrightarrow a\equiv b(mod \ \frac{m}{(c,m)} )
ac≡bc(mod m) ⇔a≡b(mod (c,m)m)
首先根据上述写出相应的式子,提取公因数c.
得出关键式子:
(
a
−
b
)
c
=
k
m
(a-b)c=km
(a−b)c=km
在整除关系中注意到
(
m
(
c
,
m
)
,
c
(
c
,
m
)
)
=
1
(\frac{m}{(c,m)},\frac{c}{(c,m)} )=1
((c,m)m,(c,m)c)=1
两式同除(c,m)即可。
7.对模m的逆:若m>=1,(a,m)=1,则存在c,使得ca同余于1模m,则c称为模m的逆。由Eulid定理有axo+my0=1,取c=xo即可。
例题:求模p=11所有元逆元:
这里就不再列举出所有的元,仅以元a=5为例,其他的同理:
由公式可得出5c同余于1模11,则5c-1=11k,所以c为9。
8.同余式组:
a
≡
b
(
m
o
d
m
j
)
j
=
1
,
2..
k
a\equiv b(mod \ \ m_j) \ \ \ j=1,2..k
a≡b(mod mj) j=1,2..k
等价于
a
≡
b
(
m
o
d
[
m
1
,
m
2
.
.
.
m
k
]
)
a\equiv b(mod \ \ [m_1,m_2...m_k])
a≡b(mod [m1,m2...mk])
这个证明比较明显,注意到mj|(a-b),则[m1,m2…mk]|(a-b),因为公倍数一定可以被整除。
这里就给出可以被9整除的充要条件。
n
=
a
0
1
0
k
+
a
1
1
0
k
−
1
.
.
.
+
a
k
n=a_010^{k}+a_110^{k-1}...+a_k
n=a010k+a110k−1...+ak
因为
1
0
i
≡
1
(
m
o
d
9
)
10^{i} \equiv 1 (mod \ \ 9)
10i≡1(mod 9)
因为10不能整数9,所以就是前面的系数要整数9,故得出
9
∣
a
0
+
a
1
+
.
.
.
+
a
k
⇔
9
∣
n
9 |a_0+a_1+...+a_k \ \ \Leftrightarrow 9|n
9∣a0+a1+...+ak ⇔9∣n
这个大家没什么感觉,但是一说到被3整除的条件大家就懂了,只要满足个数加起来被3整除就可以了,同理9也是。
10.Euler函数:这个是什么函数呢,我用简单的话语来进行总结:在模m的一个剩余类(也称同余类)以r(mod m)表示,如果(r,m)=1,那么剩余类r(mod m)就是模m的既约剩余类,那么既约个数为f(m) [原谅我five x打不出来]
11.在模m剩余类i中,Zm:a0,a1…am-1(一个完全剩余类)
在完全剩余类里面两两对模m不同余。
12.重点定理:设a,b属于整数,且(a,m)=1,那么x遍历模m一组完全剩余类,ax+b也是遍历模m一组完全剩余类。
推论:设m=m1m2,(m1,m2)=1,当xi遍历模m一组完全剩余类,xj也是,那么xij=m2xi+m1xj遍历模m一组完全剩余类。
这里以一个例题为例:
模m为35,构造m既约剩余类和完全剩余类。根据上述公式可以得出
x=7x1+5x2
那么只要让x1范围为-2~2, x2范围为-3 \ ~3即可。
13.Euler定理:
设p是素数,k>=1
φ
(
p
k
)
=
p
k
−
1
(
p
−
1
)
\varphi (p^{k})=p^{k-1}(p-1)
φ(pk)=pk−1(p−1)
定理2:设m=m1m2,且(m1,m2)=1
φ
(
m
)
=
φ
(
m
1
)
+
φ
(
m
2
)
\varphi (m)=\varphi(m_1)+\varphi(m_2)
φ(m)=φ(m1)+φ(m2)
这个公式写起来不容易理解,但是一说就明白了,首先p是素数,那么既约剩余类r,有(r,p的k次方)=1,在1,2,…p的k次方一共有p 的k-1次方个,所以
φ
(
p
k
)
=
p
k
−
p
k
−
1
=
p
k
−
1
(
p
−
1
)
\varphi (p^{k})=p^{k}-p^{k-1}=p^{k-1}(p-1)
φ(pk)=pk−pk−1=pk−1(p−1)
14. Euler定理1:
设(a,m)=1,则
a
φ
(
m
)
≡
1
(
m
o
d
m
)
a^{\varphi(m) }\equiv 1(mod \ \ m)
aφ(m)≡1(mod m)
Fermat小定理:
φ
(
p
)
=
p
−
1
∀
a
,
(
a
,
p
)
=
1
\varphi (p)=p-1\ \ \forall a,(a,p)=1
φ(p)=p−1 ∀a,(a,p)=1
则有
a
p
−
1
≡
1
(
m
o
d
p
)
a^{p-1}\equiv 1(mod \ \ p)
ap−1≡1(mod p)
例如:求7的10001方个位数
这个就相当于求n (mod 10),那么g(10)=g(2)*g(5)=4(既约个数),且(7,10)=1,所以化简得7(mod 10)
15.Wilson定理:
p是素数,r1…rp是模p的既约剩余类
∏
r
m
o
d
p
r
=
r
1
.
.
.
r
p
−
1
≡
−
1
(
m
o
d
p
)
\prod_{r\ mod \ p}^{}r=r_1...r_{p-1}\equiv -1(mod \ \ p)
r mod p∏r=r1...rp−1≡−1(mod p)
特别地:
(
p
−
1
)
!
≡
−
1
(
m
o
d
p
)
(p-1)!\equiv -1(mod \ \ p)
(p−1)!≡−1(mod p)
文件操作(杂项初步)
文件识别
1.当文件没有后缀名的时候或者后缀名无法打开的时候根据识别出的文件类型来修改后缀名打开。
~ file myfile
这个会显示出文件格式
winhex file
可以看见文件头类型。
这里总结一下常见的文件头类型
| 文件类型 | 文件头 |
|---|---|
| jpg | FFD8FFE1 |
| png | 89504E47 |
| gif | 47494638 |
| zip | 504B0304 |
| rar | 52617221 |
| html | 68746D6C3E |
| 255044462D312E |
当然也可以使用Notepad++进行查看,注意下载插件Hexview
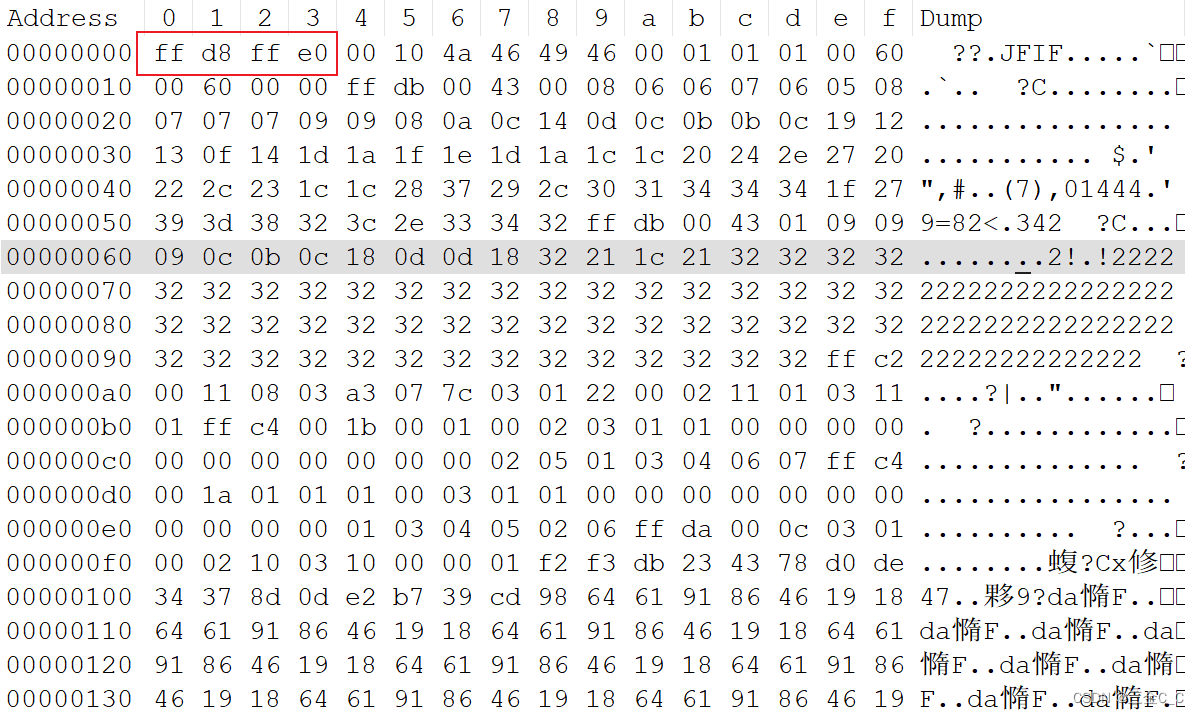
当然也可以使用010 Editor,这里就不再演示。
2.文件头残缺/错误
通常文件无法打开有两种情况,一种是文件头部残缺,另一种是文件头部字段错误。针对文件头部残缺的情况,使用winhex添加相应的文件头,针对头部错误可以进行替换。
例如
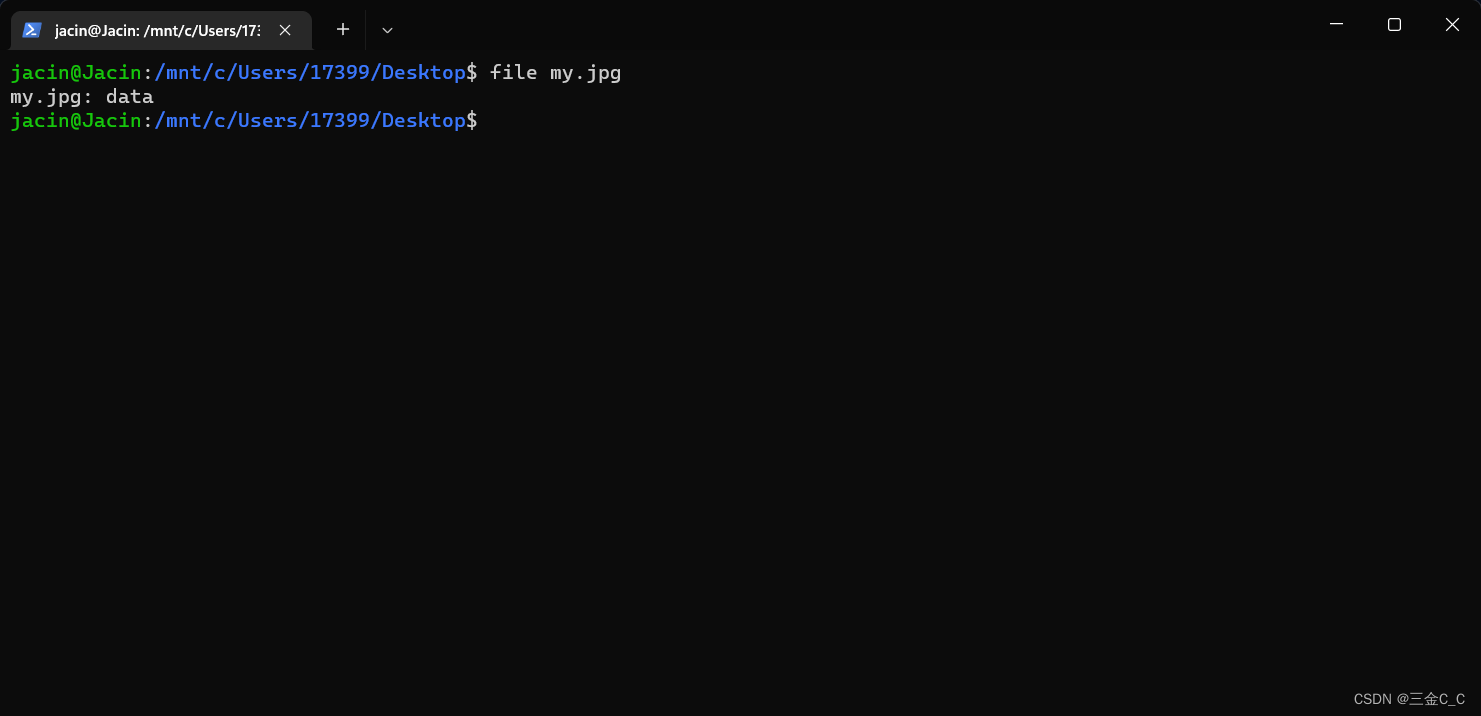
意思无法打开此文件了,那么下面进行分析。
使用010 Editor工具对文件头进行修复,插入对应的值以后,再次使用命令那么就可以看到相应的信息了。

文件分离操作
1.binwalk是Linux下用来分析和分离文件的工具,可以快速分辨文件是否由多个文件合并而成,并将文件进行分离。如果分离成功则会在目标文件的目录中,同目录下生成一个形如文件名_extracted的文件目录。
~ binwalk filename
~ binwalk -e filename

可见此文件就一个图片的文件,当然了如果遇到一个文件含其他文件的时候,会给出文件头与相应的描述。
2.如果binwalk无法正确分离出文件,可以使用foremost,将目标文件复制到kali中。
foremost filename -o 输出目录名

文件分离操作
1.当文件自动分离出错或者因为其他原因无法自动分离时,可以使用dd实现文件手动分离。
dd if=源文件 of=目标文件名 bs=1 skip=开始分离的字节数
# if=file,输入文件名
# bs=bytes 同时设置读写块的大小为bytes,可代替ibs和obs
# skip=blocks 从输入文件开头跳过blocks个块后开始复制。
文件合并操作
linux文件合并
cat file1 file2 file3 >outfile
完整性检测
md5sum filename

windows下的文件合并
copy /B file1+file2+file3 outfile
windows完整性检测
certutil -hashfile filename md5
Web前端巩固
关于最基本的点这里就不再多说了,主要是对一些选择器进行一些说明,这里就选择一部分来进行巩固。当然了代码就不再列出,关键是对一些知识做到了解。
例如在web标准中分为3个类:一个是结构、二是表现、三是行为,其实也就分别对应了三种表达形式。
在超链接中,比较重要的就是a了,所以在一些代码中,遇到a的时候需要警惕,当然了其中还包含有锚点链接和快速定位。
表格和表单的重要性不再多谈,这里值得一提的是表单需要提交的服务器是什么,也能帮助我们看到后台情况。
<form action="url" method="提交方式" name="名称">
<!--元素控件,action是指定接收服务器程序的url地址,method属性值为get,post,name是区分-->
</form>
在css中重要的就是选择器了,同时还有关于类,与类选择器差不多的就是id选择器,注意id选择器只能使用一次。
这里主要以一些选择器为例讲解:
ol li {
color: pink;
//更改ol下面的li标签
}
.nav>p {
只选择亲儿子
}
ul,div {
color: pink;
}
a {
color: gray;
td:none;
}
a:hover {
color: red;
td:underline;
}
当然了在网页布局中需要有块的概念:
常见的块元素:h1—h6 div ul ol li
特点:比较霸道、自己独占一行;高度宽度外边距以及内边距可以控制,宽度默认是容器的100%,是一个容器及盒子,里面可以放行内或者块级元素。
注意:文字类的元素不能使用块级元素,p用于存放文字,所以不能放块级元素,块级标签不能放其他元素。
行内元素:
a strong b em i del s ins u span(最典型的行内元素)
a {
display: block;(块级元素)
display: inline(行内元素)
text-indent: 2em (首行缩进2)
}
行内块元素
有几个特殊的标签:
img input td 同时具有块元素和行内元素的特点。
特点:高度和行高边间距可以控制
默认宽度就是内容的宽度
一行可以显示多个
关于css还有三大特性,分别是层叠性、继承性、优先性。
选择器权重如下表所示
| 选择器 | 选择器权重 |
|---|---|
| 继承或者* | 0,0,0,0 |
| 元素选择器 | 0,0,0,1 |
| 类(伪类)选择器 | 0,0,1,0 |
| ID选择器 | 0,1,0,0 |
| 行内样式style | 1,0,0,0 |
| !important | 无穷 |
边框border
有三部分组成:边框宽度 边框样式 边框颜色
以上就是本周的学习部分。





















 1942
1942











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








