插值理论及其在海啸与潮汐问题中的应用

系统简介

由于持续发展的科学技术，潮汐发电这一功能为人类提供了前进的动力以及发展的潜力。不仅使用电得到了满足，还能够将化石燃料等非再生能源的使用减少，起到了环境保护的作用，然而极为重要的问题就是研发出新的环保电站。虽然潮汐能的开发前景极为广阔，但是就我国而言，对于潮汐能的开发量不到1‰，所以这是我国亟待解决的问题。
根据星下观测点各主要分潮，利用最小二乘法和切比雪夫多项式法去求解特定星下观测点的潮汐调和常数，得到主要分潮的相关数据，但此时得到的调和常数误差较大，于是通过三次样条拟合函数和克里金插值方法将振幅和迟角进行重新插值拟合，将得到的结果画图，从而得到同潮图。
本文以插值理论为基础，研究了提取潮汐调和常数、对验潮站数据MATLAB上使用三次样条插值、克里金差值等方法绘制同潮图。海洋潮汐同潮图的绘制需要获取潮汐调和常数，在描述潮汐潮流特征过程中，潮汐调和常数的获取是重要的一项科学研究，直接影响海洋潮汐同潮图的绘制。同潮图的绘制能够帮助人们更好地把握海域分潮振幅以及分潮传播规律，为全方位的海洋开发与利用等工作提供信息参考。
关键词 潮汐调和常数 三次样条插值 切比雪夫多项式插值 克里金插值

1.绪 论

1.1研究背景与意义
海洋在地球面积之中占有七成多，海水遮盖着大多数的地表。海水最为根本的一种运动方式就是潮汐运动，潮汐运动也就是海水的周期性运动，其产生是重点受到了天体引潮力、季节这一地理变化以及地球自转的影响。潮汐是海水水位的垂直运动，潮流则是海水的水平运动。通常状况下，潮流速度比水位垂直的运动速度大很多，潮流的变化与潮汐的变化作比较，前者则极为复杂。中月引潮力是潮汐所形成的重要原因，这是由于月球、太阳这两者对潮汐所产生的影响作用与其他相比是最大的[1]p1。分析并探究潮汐，能够对环流、风暴潮等其余有关的海洋现象的分析与探究有着直接、间接的影响作用。也就是说，在大陆架浅海的海洋之中，对潮汐以及潮流进行相关的研究在一定程度上具有重要意义。
人类进行生产生活以及实践最为频繁的区域为，海岸附近、河口区域这两个地方。然而在这个区域之中，其具有着极为明显的潮汐现象，也就能够直接、间接的对人类的生产生活以及实践产生影响作用。分析以及研究潮汐潮流，能够为交通运输、能源的开发与利用、海口创建等供应着极为便利的条件[2]p2。如：培育水产生物、盐的制造、以及潮能给发电等有关的活动，都和潮汐潮流现象之间有着密不可分的联系。
每天都会出现潮汐现象，长此以往、循环往复，不仅为人类提供了航海的便利，还为人类的制盐、环保等方面提供便利的条件。由于持续发展的科学技术，潮汐发电这一功能为人类提供了前进的动力以及发展的潜力[3]p1。不仅使用电得到了满足，还能够将化石燃料等的非再生能源的使用减少，起到了环境保护的作用，然而极为重要的问题就是研发出新的环保电站。但是就我国而言，对于潮汐能的开发量不到1‰，然而潮汐能的开发前景极为广阔。
牛顿对于万有引力的发现，顺利的将潮汐这一现象进行了阐明。也就是说所具备的前提极为理想时，天体能够对地表水形成有一定的万有引力，从而导致“平衡湖面”在海洋的表面产生[4]p4。
近代对于潮汐的分析与探究，就是通过万有引力定律所进行实施的。之后又随着拉普拉斯等相关研究者的分析与探究，不断地对其进行改进完善。1950年之后，电子计算机的大规模运用，以及不断的与现实情况相结合，如深、浅海等诸多原因。从而使得所得出的数据不断趋于准确。从牛顿的理论中得出，潮汐现象的产生就是在地球之中月亮、太阳这两者引力分布的不同[5]p2。
在我国公元前2世纪的早期相关资料中，就有了月望(满月)那天就能够观看到极为壮丽的海潮的有关记录。古代王充的诗句之中“涛之起也,随月盛衰,大小、满损不齐同”，从中能够看出潮汐、月球这两者之间的依靠关系[6]p5。其中对涨潮时间变化进行有关描述出现在封演《封氏见闻记》之中。之后准确叙述潮汐的还有张君房、郭守敬等人。李约瑟(1900-1995)也曾说过，在近代以前，中国对潮汐现象的认知与欧洲相比，中国则更受一筹。
1970年之后，我国开始运用计算机。从而促使杨景飞等人，所分析探究的潮汐数值模拟当面获取了相当大的成绩，由于持续增强的大型计算机计算功能，其数值计算在潮汐的分析探究中有着极为重要的影响作用。
1.2 研究现状
迄今为止的潮汐分析和预报最常用的方法是调和法，而调和分析方法的主要思路是将天间的各种运动分解为一组余弦无穷级数[7]p6。首先是依据预报所需的精度要求，选取其主要的级数项，然后通过实际潮汐测量值来求解出各个级数项的初始角度以及系数，获取了这些数据之后再依据时间来预测后面某一时刻的潮高。
从历史上各分潮调和常数的获取方法来看，曾经首选的方法是通过对已近获取到的观测结果进行插值，但是这种方法逐渐被数值模拟方法所取代[8]p4。
本文基于992年到2017年的卫星高度计海面高度异常资料，选取了中国南海海域进行分潮提取。通过函数插值的方法计算对某一点上的调和常数进行插值，得到某一地点分潮的平均振幅和迟角值来进行对比。
1.3本文主要研究内容
第一章是着重对本文的研究背景、意义，还有国内外研究背景进行了阐述。第二章是潮汐潮流参数与数值分析方法的介绍，第三章研究问题的提出与分析，第四章建立数学模型，编写代码，给出了潮汐同潮图并做了简要分析。

2.插值方法

2.1插值方法的描述
常规插值工作的进行需要依靠特定公式的支持来实现推导与分析，假定为上的函数，在区间上取的互异点，这些点在上对应的函数值分别为。得到的函数的表如下表1：

此时点被称为插值基点，区间被称为插值区间。函数就属于是对应着的插值函数。差值的误差一般可以表示为式子
（1）

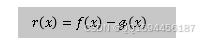
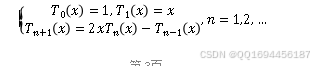
插值的本质就是经由已经知道的插值基点完成与紧密相关的插值函数的构建，如此原本未知的点也能够经由的函数值加以取代，得到相关值的信息内容[9]p7。

上述得到的两组点就是切比雪夫点，这些点正好是单位圆周内等距状态分布的横坐标，在端点位置呈现密集分布的状态选择切比雪夫法实现插值分析，则能够保障插值区间内的最大误差满足最小化的需要。假定其插值点对应是： 表征的是次Lagrange多项式，则其插值余项对应表现是：

2.3三次样条插值
如果，并且各个内存在的十三次多项式，是给定节点，则称是节点上的三次样条函数，若在节点上给定函数值,并成立则称为三次样条插值函数[11]。
2.4克里金插值
在地理统计分析中，克里金插值法是用到相对较多的内插方法，属于是空间局部插值。运用该方法进行插值分析期间，需要基于对观测资料全部相互关系进行深刻把握的情况下来赋予合理的权重系数，进而经由加权平均处理的方式获得估计值。

式中，是和的协方差函数。 3.潮汐潮流参数与数值分析方法

3.1数据来源及符号说明
3.1.1数据来源
本次分析的数据源自我国近海周边的验潮点，涵盖9个分潮的潮汐调和常数，56个验潮点详细的资料信息，并且给定与分潮相关的潮汐调和常数。基于国际上长期用到的数据分析情况，能够将其区别是天文分潮、气象分潮、天文-气象分潮以及浅水分潮四种类型。
本文中的地形数据则是来自于ETOP5，全球分辨率为，地形区域为。至于高度计资料，只涉及到TOPEX/POSEIDON卫星高度计资料与潮汐相关的研究。

3.2.3分潮初相位的计算
年月日时刻对应着的天文初相角是：
(11)

其中：为Doodson数，

式中为1900年至年的闰年数，；为从年1月1日进行预算的累积日期序数0，为时间（单位：小时）。以上各式中的单位是度。
3.2.4和的计算
考虑到伴随时间的改变，以及变化的程度相对较弱，故而，能够选择资料序列内的中间时刻展开运算分析。
各分潮的、的具体计算公式如下：
(12)

对于、、、、、、、、、分潮的和参考上式展开运算，而其余分潮则参照其分潮组合的方式来展开运算，但分潮的和由以下公式计算得出：
(13)

 (14)![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/9dbd047c1b714bf0be329ce16b0f2bca.png)

3.2.5最小二乘法
对公式，选择三角函数内具有的和差化积性质展开变换处理：

对应个分潮，则有：
(15)

假设某一星所得到的观测点存在个时刻的观测信息，则：

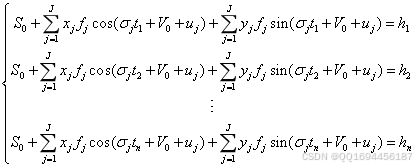
为更大程度上降低噪声带给分析结果方面的消极影响作用，让调和常数能够无限靠近真值，实际实现的潮汐分析工作期间，会期待用到更多数量的观测数据来展开研究工作。因此，方程的数量一般远大于未知数的数量。针对此般矛盾方程组，能够依靠最小二乘法的方式来做以求解与分析。
最小二乘法的核心就是能够获取到一组解，保障拟合值以及实际值两者差值的平方和是最小的状态，即：
(16)

根据多元函数微分的理论，这要求相对于各未知数的偏导数均为0，即：

如此就能够获得有关分潮调和常数对应着的线性方程组，得到与之相关的调和常数值。
3.2.6切比雪夫多项式插值获取调和常数
根据卫星上所给出的tp轨道上的数据，由上述的调和分析方法所获取的研究区域上的观测点的调和常数。然后对所获取到的调和常数，再采用切比雪夫多项式插值法得到研究区域范围内各个点对应着的调和常数信息。
选取分潮上观测数大于等于300次的观测点的数据，以确保调和分析结果的准确性。选择5、10、15、20次切比雪夫节点展开必要的多形式插值处理操作，并用MATLAB作图，得出图1，图2。表2给出沿某轨道的插值结果和调和分析结果的绝均差：
表2 振幅H与迟角G插值绝均差信息
次数 5次 10次 15次 20次
0.72 0.63 0.58 0.57
11.37 10.03 16.67 8.86

图1分潮振幅H展开插值对比分析

图2分潮迟角G展开插值对比分析
参照图1、图2信息明确，各个次数得到的切比雪夫插值多项式曲线及其数据点均呈现出很好的一致性表现。联系表1，对比四次插值的信息明确，5次插值获得的分潮振幅具有最大的绝均差，15次插值所得分潮迟角具有最大的绝均差20次的插值综合效果好于其他次数的插值效果，所以，后续的研究中，选择20次切比雪夫多项式插值的方式针对其余轨道存在的调和常数进行插值分析。

附 录
% 计算切比雪夫多项式插值节点，s1,t1为区间，n为节点个数
function x = chebyshev( s1,t1,n )
x = zeros(1,n);
for i = 1:n
    x(n-i+1)=(s1+t1)/2+(t1-s1)/2*cos((2*i-1)*pi/(2*n));
end
end

% 使用切比雪夫多项式插值预测调和常数H，G并作图，返回均方误差和绝均差
function [ sse1, am1 ] = cheInHg( x1, lon1, H, G, Hc, Hs )
n = length(x1);
disp(n)
lhgcs = [lon1, H, G, Hc, Hs];
lhgcs = sortrows(lhgcs,1);
xx1 = min(lon1):0.1:max(lon1);
yc1 = Lagrange(x(:,1), x(:,2),xx1);
ys1 = Lagrange(x(:,1), x(:,3),xx1);
yce1 = Lagrange(x(:,1), x(:,2),lon1');
yse1 = Lagrange(x(:,1), x(:,3),lon1');
yc1 = yc1';
ys1 = ys1';
yce1 = yce1';
yse1 = yse1';
sse1_hc = sum((yce1 - Hc).^2);
sse1_hs = sum((yse1 - Hs).^2);
am1_hc = mean(abs(yce1 - Hc));
am1_hs = mean(abs(yse1 - Hs));
HH = sqrt(yce1.^2+yse1.^2);
GG = acos(yce1./HH);
GG = rad2deg(GG);
for i = 1:length(GG)
    if(yse1(i) < 0)
        GG(i) = 360 - GG(i);
    end
end
LHG = [lon1, HH, GG];
LHG = sortrows(LHG, 1);
sse1_h = sum((HH - H).^2);
sse1_g = sum((GG - G).^2);
am1_h = mean(abs(HH - H));
am1_g = mean(abs(GG - G));
sse1 = [sse1_h, ss1e_g, sse1_hc, sse1_hs];
am1 = [am_h, am_g, am_hc, am_hs];
% subplot(2,2,1)
% scatter(lhgcs(:,1), lhgcs(:,4), '.');
% hold on
% grid on

4.问题的提出和分析

4.1问题的准备
为了得到南海各主要的分潮的同潮图和观测点的经纬度和振幅迟角，我们采用切比雪夫多项式和最小二乘法求得的潮汐调和常数，但是这个时候所得到的调和常数误差比较大，所以再次选择使用插值法对振幅和迟角进行差值或拟合，将得到的结果绘图，从而得到我们所需要的同潮图。选择插值法实现的预测模拟中，经插值所得构建得到南海各个主要分潮的同潮图，依靠测验点所得调和常数来展开检验分析，获得最终的评价结果。
4.2 问题的分析
在整个分析工作中，关键就是确定适合的插值方法来绘制各个分潮的同潮图。基于正压潮相关的调和参量，引入切比雪夫多项式插值法，针对各分潮得到的调和参数值完成插值，从而绘制出其正压潮振幅和迟角的同潮分布图，最后利用验潮站的数据，对插值后得到的靠近验潮站的数据进行评价和检验。
需要首先选择适合离散点数据的插值方法，然后建立该插值方法的数学模型，然后再利用该插值方法制作出各主要分潮的同潮图，最后对同潮图的评价以及评价结果的分析。
参照沿轨道位置的星下观测点所得到的海面高度异常值信息情况，获得全部星下观测点内各个主要分潮对应着的潮汐调和常数情况。然后，根据所有轨道上任意点处的潮汐调和常数进行插值处理得到整个平面研究区域内的潮汐调和常数数值。
本章经由多项式拟合处理的方式来针对沿轨道分布的各个分潮相关的潮汐调和常数实现的正压潮以及内潮相关的分离处理，引入插值法绘制获得南海诸多主要分潮同潮图，并且针对结果情况展开深入的研究与分析。

5.模型建立与求解

5.1 模型建立
需要将海南每个主要分潮的同潮图获取，那么把南海地区中任意一点的每个主要分潮的潮汐调和常数进行计算得出，根据区域内已知的潮汐调和常数，采取怎样的方法获得整个平面内任意点的潮汐调和常数是值得商榷与评估的。
数据插值法所要求的就是要采用原始数据样本，而对差值结果产生直影响的是所采用的样本数据的质量。再依据验潮站观测数据所得的潮汐调和常数分别与两种插值方法所得的验潮站处的潮汐调和常数最对比并分析其结果。
5.1.1三次样条插值模型
设在节点处的二阶导数为

(17)

其中

也就是待定参数，能够达到线性方程组的要求
(18)

方程组(18)是含有个未知数的线性方程组的构成就是个方程，对其解不能够有所确定。那么就必须将两个条件进行一定的补充。通常条件下，所补充的条件在插值区间的两个端点上，替代的符号为：

求解过程：
1、将方程(2)与端点条件结合，解出关于的线性方程组。

2、在方程(2)当中，将放入，那么每个子区间的表达形式便会获取，其方程组的求解过程就是：

5.1.2克里金插值的数学建模
若区域化变量能够使二阶平稳假设以及本征假设得到满足，是它的数学期望，也就是说协方差函数、变异函数两者都具有。即：

若二阶平稳的随机函数就是，取样在其第个的位置：,点处的估计量为：
(19)

这里权重系数的是，所代表的是空间样本点中的观测值，且其对这一计值的贡献水平。计算权重系数是克里金算法的根本，权重系数计算要对两个前提进行满足：

5.2 模型求解结果
5.2.1基于三次样条模型求解
选取特定的坐标，由于坐标数量很多，误差较大，本文选取具有代表性的13组数据。先对主要分潮中的分潮进行研究。所开展的三次差值是经、纬度，振幅，获得数值，再将数值与经度，纬度进行画图，得到了一张三维图，由于三维图无法具体展现等振幅线的变化，所以将三维图投影到平面，得到了下图3：

图3 分潮的振幅同潮图
类似的方法，得到了分潮的迟角同潮图（图4），分潮的振幅同潮图（图5），迟角同潮图（图6），分潮的振幅同潮图（图7），迟角同潮图（图8），分潮的振幅同潮图（图9），迟角同潮图（图10）：

图4 分潮的迟角同潮图

图5 分潮的振幅同潮图

上面图像获取之后，检测的进行就要通过验潮点的调和常数。因为不能找到完全相同的经纬度，所以此时本文采用的是相近位置的坐标，利用原始数据，得到振幅，迟角，即下表3：
表3 13个近似验潮点的坐标和调和常数
位置 误差

100.1 2.6 120.00 153.7 18.1 8.3
100.35 5.42 56.80 24.69 3 6
101.25 2.9 121.60 165.42 9.5 2
102.25 2.18 60.40 238.98 2 9.4
104.47 10.37 9.80 118.9 2 14
106.8 10.67 5.40 75.98 1 5
107.95 21.2 25.40 124 9.8 4
110.6 20.95 78.80 312.5 8 19.2
113.3 3.52 13.40 36 3 2
115.6 6.2 23.50 320 8 11
119.9 15.77 11.70 263.1 4.5 2
120.6 14.39 17.30 311.7 4 7.2
121.4 23.12 51.00 166.1 4.4 3
经有效的比对，调和分析的结果总体分布与论文、验潮站所得出的结果大致一样，这就说明了克里金插值这一方式的所具备的优势极大。同时对于不同水深区域，在近岸区域验潮站的插值结果更加准确，在深海中高度计调和分析插值结果细节表现较好。
将上述坐标带入图中，可以发现此坐标点所对应的振幅和迟角与实际验潮点的数据相差不大，两者差值同样在表2中，从差值中可以得出本文模型三的拟合结果非常可靠。

结 论

经由调和常数来实现切比雪夫多项式插值处理，运用得到的差值多项式能够预估轨道内任意点对应着的调和常数值。在多项式拟合过程中，拟合次数过高会导致过拟合的情况，选择合适的次数后，利用参考文献可以对区域内任意一点插值，有助于第三问同潮图的绘制。最终通过对比插值结果得出插值次数在20次左右的效果较好。
克里金插值模型能够在数据网格化处理期间，将空间离散数据具有的空间相关性特征考虑在内，使得整个插值结果更具科学性与合理性，与实际的情况更为贴近。
三次样条插值模型，利用潮汐调和模型进行数值模拟比实地测量少耗费资源和劳力。求解过程中增加了检验模型，体现建模的严谨性。模型建立过程中采用图形，数表相结合，使数据直观、简明。
虽然调和分析的方法距今已有好多年，但有些问题仍然没有解决。对于浅水港口来说，在求解问题中应该考虑由分潮和由气象等因素引起的扰动，精确分析结果。对数据处理过程中，数据量太大，应先对数据进行筛选，选取代表性数据，使最后结果更准确，加大模型精度。在浅水中运用高度计资料进行调和分析时,由于潮汐的浅水效应和地形效应,其精度大大地降低了,就会导致很大的预报误差,需要进行潮汐订正。
对于其他插值方法，其实我们还可以使用模型验证方法来选取其中的最佳函数：
交叉验证使用所有数据对趋势和自相关模型进行估计。它会每次移除一个数据位置，然后预测关联的数据值。例如，有 10 个数据点。交叉验证会省略一个点，然后使用剩余的 9 个点计算此位置的值。将省略点位置的预测值与实际值相比较。然后对第二个点重复此过程，以此类推。交叉验证会对所有点的测量值和预测值进行比较。完成交叉验证后，得到所有已知点与其预测值之间的偏差， 这个所有点的偏差从某种程度上讲就为我们提供了整个预测方法是否合理的依