关于碎纸片拼接复原的算法研究

于 2023-08-14 22:04:43 发布
阅读量3.2k 收藏 42
点赞数 6
文章标签： 算法 数学建模 matlab 聚类
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Qianni1027_Jiang/article/details/132286267
版权

关于碎纸片拼接复原的算法研究

摘要

碎纸片的自动拼接技术是一个新兴的课题,也是图像处理与模式识别领域中一个较新却很典型的应用,它通过扫描或者图像提取技术来获得一些碎纸片的形状、颜色等信息，然后利用计算机进行相关的处理分析,从而实现对这些碎纸的拼接复原。当碎纸片数目很少时,可以通过纯手工把它们拼起来,但当其数量达到一定程度甚至几百上千,就会非常耗费人力物力,而且容易对碎纸造成破坏。故利用计算机取代繁琐重复的劳动是行之有效的方法[1]。

本文围绕几种不同类型的碎纸片拼接复原，建立碎纸片距离模型、旅行商模型和聚类分析模型，结合人工干预对几种不同类型的碎纸片拼接复原问题进行分析求解。

针对问题1，首先使用Matlab将碎片导入，将图像数值化，进而二值化，建立每两张碎片左右两侧的Jaccard距离模型，通过碎纸片最左侧的特征找到第一张碎纸片，建立旅行商模型，利用贪心算法确定最邻近距离，取最邻近距离的图片作为邻接图片求解子问题的最优路线，得到碎纸片拼接复原图及碎纸片序列。

针对问题2，首先使用Matlab将碎片导入，将图像数值化，进而二值化，以碎纸片的行平均值作为特征向量，使用Correlation**距离进行ward层次聚类，辅以人工干预，将碎纸片同一行的碎片分为一组，与问题1相同进行建立每两张碎片左右两侧的Jaccard距离模型，通过碎纸片最左侧的特征找到第一张碎纸片，建立旅行商模型，利用Lingo规划算法求最佳哈密尔顿圈**，由于每张碎纸片过小，通过Jaccard距离模型求解的最佳哈密尔顿圈未必正确，需要进行人工干预，找到每张碎片的正确邻接碎片，得到每行的碎纸片拼接复原图及碎纸片序列，再将拼好的行碎片转置，与问题1相似找出拼接顺序，得到总的碎纸片拼接复原图及碎纸片序列。

关键词：二值矩阵；Jaccard距离；旅行商模型；相关距离；系统聚类

目录

关于碎纸片拼接复原的算法研究

摘要

目录

一、问题重述

1.1 问题背景

1.2 目标任务

二、问题分析

2.1 数据分析及预处理

2.2 具体分析

2.1.1 对问题1的分析

2.1.2 对问题2的分析

三、模型假设

四、符号说明

五、模型的建立与求解

5.1 问题1模型建立与求解

5.1.1 特征因子的构建

5.1.2 Jaccard距离的定义

5.1.3 旅行商模型

5.1.4 复原模型以及算法

5.1.5 复原结果

5.2 问题2的模型建立与求解

5.2.1 相关距离

5.2.2 ward层次聚类

5.2.3 改进旅行商模型

5.2.4 确定头碎片

5.2.4 行拼接与列拼接

5.2.5 复原模型以及算法

5.2.6 人工干预

5.2.7 复原结果

5.3 问题1与问题2的区别与联系

六、模型的评价与推广

6.1 模型评价

6.2模型推广

附录

1.问题1

（1）拼接复原图

2.问题2

（1）聚类结果

（2）拼接复原图

（3）源码

一、问题重述

1.1 问题背景

破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。传统上，拼接复原工作需由人工完成，准确率较高，但效率很低。特别是当碎片数量巨大，人工拼接很难在短时间内完成任务。

随着计算机技术的发展，人们试图开发碎纸片的自动拼接技术，以提高拼接复原效率。

1.2 目标任务

问题1：对于给定的来自同一页印刷文字文件的碎纸机破碎纸片（仅纵切），建立碎纸片拼接复原模型和算法，并针对附件1、附件2给出的中、英文各一页文件的碎片数据进行拼接复原。如果复原过程需要人工干预，请写出干预方式及干预的时间节点。

问题2：对于碎纸机既纵切又横切的情形，请设计碎纸片拼接复原模型和算法，并针对附件3、附件4给出的中、英文各一页文件的碎片数据进行拼接复原。如果复原过程需要人工干预，请写出干预方式及干预的时间节点。

问题3：上述所给碎片数据均为单面打印文件，从现实情形出发，还可能有双面打印文件的碎纸片拼接复原问题需要解决。附件5给出的是一页英文印刷文字双面打印文件的碎片数据。请尝试设计相应的碎纸片拼接复原模型与算法，并就附件5的碎片数据给出拼接复原结果。

二、问题分析

2.1 数据分析及预处理

因为颜色在计算机中用数值表示，故将附件中的每一张bmp碎片用一个矩阵来表示。又碎片的颜色只有黑白灰三种，故建立的矩阵即为灰度矩阵，只要对每张图的灰度矩阵做处理比较即可。

考虑到由于每个字的灰度多种，会使相邻图的一一匹配对数下降，故将灰度矩阵二值化为只有0（黑色像素）和255（白色像素）的矩阵。我们所说的图像的二值化，就是将本题中的灰色像素点转化为白色或者黑色像素点。

2.2 具体分析

2.1.1 对问题1的分析

问题1为一维复原问题，仅考虑碎片左右（x轴方向）端的特征即可。

首先需要计算每两张碎片相邻边缘像素列01值的匹配度，寻找与被匹配图存在最高匹配度的碎片，即可判定为被匹配图的相邻碎片。

建立匹配度矩阵后需要找出文章的最左端，由于原文页边距一定为空白部分，所以可以通过碎片最左端的数字特征来寻找，最左端空白区域最多的那张碎片即为文章的最左端。

找出最左端的碎片，并根据每张碎片的最优后继碎片就能以此从左往右拼出全文。

2.1.2 对问题2的分析

问题2属于二维复原问题，不仅考虑碎片左右（x轴方向）端特征，还需考虑上下（y轴方向）端特征。

首先我们计算每张碎片的特征向量，使用特征向量进行系统聚类，目的是将208张碎片同为一行的碎片分为一类，共11行。

然后针对每一行碎片进行拼接处理，仍然建立Jaccard距离矩阵，此时问题从二维转换为一维，但由于碎片较之问题1的碎片在高度上大大减小，故需使用更加精确的寻找最左端碎片、寻找后继碎片方法。

图 2.1.1 问题分析

三、模型假设

  • 假设文章为黑白双色打印。破碎文件形状规则，大小一致。

  • 假设不存在字迹缺失问题。

  • 假设人工干预时的每次判断均是正确的，不存在手误问题。

  • 碎片进行了横向及纵向切割,假设在切割之后,图像不存在平移、旋转、缩放等多种变换,图像边界平滑,像素信息保持完整[2]。

四、符号说明

本文涉及到的主要变量符号说明：

表格 1符号说明

注：未说明的变量以其在符号出现处的具体解释为准。

五、模型的建立与求解

5.1 问题1模型建立与求解

5.1.1 特征因子的构建

为了叙述以及编程的方便，在分析过程中给予附件碎片新编号，附件的碎片编号去除无效0位后统一加上1作为新编号，如bmp000的新编号为bmp1 。

汉字是由各种特定的点和线构成的,在笔画上有一定的连续性。本文算法就是基于文字的连续性,对碎片像素矩阵的最左侧和最右侧的列向量做相关,遍历所有图片寻找相关度最大的那张[3]。

碎片bmp1,bmp2,bmp3,\cdots ,bmp19对应的二值矩阵分别记为A_{1},A_{2},\cdots ,A_{19},。特征因子x_{1}^{j},x_{2}^{j}(j=1,2,\cdots ,19)分别为A_{j}的左、右端列向量，可看作1980维空间内的点，则共有19\times 2个列向量。

5.1.2 Jaccard距离的定义

5.1.3 旅行商模型

旅行商问题（Traveling Salesman Problem，TSP），是最基本的路线问题，单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点，需要求出最短距离。可以从距离矩阵中产生一个近似最佳解的途径，有节省法、插入法、途程改善法、合成启发法等求解途径。

使用Jaccard距离建立距离矩阵d，利用贪心算法确定最邻近距离，取最邻近距离的图片作为邻接图片，利用贪心算法继续求解子问题的最优路线。得到排序结果 index，按照 index得到新碎片顺序矩阵 newpict，即为复原结果。

5.1.4 复原模型以及算法

step1：将19张碎片导入，建立一个矩阵pict存储这些碎片。

step2：使用19张碎片的灰度矩阵得到对应的二值矩阵，并将其存放在集合 B中。

step3：建立一个用于存放各碎片最左端和最右端的二值矩阵 C，将集合B中的矩阵经过处理得到矩阵C 。

step4：计算每两张不同碎片间的Jaccard距离，并定义一个矩阵d 记录距离。

step5：利用最优化的方法为第 张图向右找到它的最优匹配第 k张图，并建立一个矩阵index存储。

step6：算出19张碎片最左端的留白长度，得到长度最大的碎片即为原图最左端的碎片，编号为indexF 。

step7：根据 index矩阵，以最左端碎片为起点，从左往右拼出全文，建立 newpict矩阵存储新的碎片顺序。

step8：根据 newpict矩阵将完成拼接的碎片保存。

       

图 5.1.1 问题1复原模型流程图

5.1.5 复原结果

以下给出附件1和附件2的复原图片拼接序号。

表格 2问题1附件1图片拼接序号

8

14

12

15

3

10

2

16

1

4

5

9

13

18

11

7

17

0

6

表格 3问题1附件2图片拼接序号

3

6

2

7

15

18

11

0

5

1

9

13

10

8

12

14

17

16

4


5.2 问题2的模型建立与求解

5.2.1 相关距离

Correlation距离主要用来度量每两个碎片特征向量的线性相关程度。

将每个碎片的行平均值作为特征向量，相关系数是衡量两个碎片之间特征向量之间相关程度的一种方法，取值范围 。相关系数的绝对值越大，表明碎片X和Y的相关程度越高。当取值为1时表明正线性相关，-1时表明负线性相关。

5.2.2 ward层次聚类

对灰度图像或彩色图像中的相似灰度或色度合并的方法称之为聚类，通过聚类将图像表示为不同区域即所谓的聚类分割方法。此方法的实质是将图像分割问题转化为模式识别的聚类分析[5]。

聚类和分类不同,聚类是根据数据特征的不同而将数据划分为若干个簇或类,其所要求划分的类是未知的。通常聚类问题被看作是一种优化问题,用于对目标函数或者准则函数进行优化[6]。

聚类分析以相似性为基础，在一个聚类中的模式之间比不在同一聚类中的模式之间具有更多的相似性。对碎纸片进行拼接复原，每一行具有较高的相似性，通过层次聚类中的ward方法将208张碎纸片分为11组，通过人工干预将碎纸片均分。

Ward聚类过程：

① 计算每个cluster的ESS：

② 计算合并每两个cluster后总的ESS。

③ 取合并后ESS最小的两个cluster进行合并，重复上述步骤直到合并完所有cluster。

5.2.3 改进旅行商模型

由于问题1中每个碎片大小为1980*72 ，问题2中每行中的每个碎片大小为 180*72，较之问题1，最优子结构性质较不明显，所以利用Jaccard距离矩阵时，使用贪心算法确定最邻近距离会产生较大误差，故使用Lingo规划算法求最佳哈密尔顿圈。

5.2.4 确定头碎片

5.2.4 行拼接与列拼接

5.2.5 复原模型以及算法

 

图 5.2.1 问题2复原模型流程图

5.2.6 人工干预

由于纸片较小，将碎片的行平均值作为特征向量和两碎片间Jaccard距离的定义未必能准确反应原来的情况，这是对结果作为人为干预，使拼接效果更好。

1.聚类误差

找出类元素个数大于19的类，找出不属于该类中的元素，将其移动到元素个数小于19的类中，使所有类的类元素个数均为19。

2.后继元素误差

观察找出不能完美衔接的图片，改变前一张碎片的后继元素值，重复进行此操作，直至肉眼无法观察明显错位为止。

5.2.7 复原结果

以下给出附件3和附件4的复原图片拼接序号，其聚类结果分布见附件。

表格 4问题2附件3图片拼接序号

141283159821991351273160203169134393151107115176
94348418390471214212414477112149971361641275843
12513182109197161841101876610615021173157181204139145
29641112015921804837755544206101049817217159
7208138158126681754517401375356931537016632196
89146102154114401512071551401851081174101113194119123
4954651431862571921781181909512928911881411122
611978676999162961317963116163726177205236
168100766214230412314719150179120861952618718
381484616124358118912210313019388167258910574
711568313220017803320219815133170205851521652760

表格 5问题2附件4图片拼接序号

1917511154190184210418064106414932204653967147
201148170196198941131647810391801012610061728146
8651107294015818698241171505595892303746127
19194931418812112610515511417618215122572027116582
159139112963138153533812312017585501601879720331
204110811613673362071351576431994517379161179143
2082174961119331421686216954192133118189162197112
708460146817413719584717215696239912290185109
1321819569167163166188111144206313034131102527178
17142662051015774145831345518563516918315244
81771282001315212514019387894872121771240102115

5.3 问题1与问题2的区别与联系

问题1为一维复原问题，仅考虑碎片左右（x轴方向）端的特征即可；问题2属于二维复原问题，不仅考虑碎片左右（x轴方向）端特征，还需考虑上下（y轴方向）端特征；且问题2碎片较之问题1的碎片在高度上大大减小，故需使用更加精确的寻找最左端碎片、寻找后继碎片方法。

下面用流程图直观地表达该两个问题算法大致步骤。

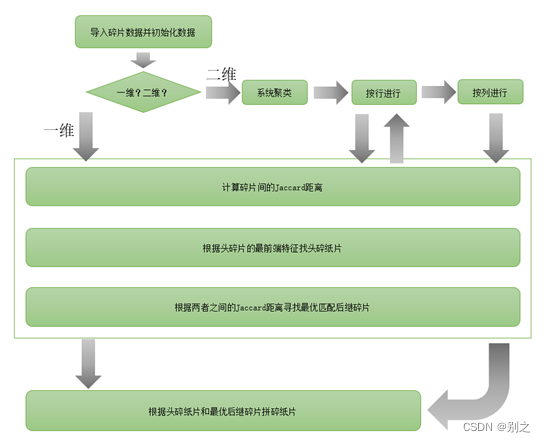
图 5.3.1 问题1、2的算法大致流程

六、模型的评价与推广

6.1 模型评价

本文中的模型对于解决纵向碎纸片拼接问题，其正确率能达到100%，拼接效果较好，且不需要人工干预。

对于问题二中的横纵切割的碎纸片拼接问题，在无人工不预的情况下，具有一定的拼接误差，需要通过人工协助分类以及排序，其拼接效果不是很好。

对于以上两个种类型的拼接问题，中文拼接成功率大于英文拼接成功率。

6.2模型推广

本文种所介绍的碎纸片拼接问题高限在方近切割上，但在现实生活中，往往纵向垂直的切割和横向水平的切割很难做到，因此在本文的基础上，可以考虑斜向切割的碎纸片拼接问题，通过将斜向的碎纸片摆正等操作，将问题转换为本文的水平与竖直切割的醉纸片拼接问题。

本文的碎纸片字迹残边非常清晰，但在现实生活中，一般通过切割的碎纸片的边缘将会存在“毛刺”，使得识别碎纸片的字迹残边的准确率大大降低，因此，可以在本文的基础上对图片进行降噪处理，使其能够处理更为一般的切割情形。

七、参考文献

[1].刘威,王军民,刘克勤.基于边缘匹配的纵向碎纸拼接方法[J].计算机与现代化,2019(02):55-59.

[2].曾晓晶,樊斌.基于规则形状的碎纸片自动拼接技术研究[J].信息与电脑(理论版),2015(24):115-116+119.

[3].刘亚威,王军民,刘威.基于相关矩阵的纵向碎纸拼接方法[J].计算机与现代化,2019(10):43-47.

[4].崔婧. 基于Jaccard的植物叶片图像识别方法研究[D].兰州大学,2021.DOI:10.27204/d.cnki.glzhu.2021.000738.

[5].贾海燕. 碎纸自动拼接关键技术研究[D].国防科学技术大学,2005.

[6].侯颖,何翼,刘合财.基于聚类分析的规则文字碎片拼接技术研究[J].贵阳学院学报(自然科学版),2014,9(04):18-19.DOI:10.16856/j.cnki.52-1142/n.2014.04.006.

附录

1.问题1

（1）拼接复原图
附件1附件2
 （2）源码
%% I. 清空环境
clear
clc
close all
%% II. 导入bmp格式图片，基于阈值将图像转换为二值图像，取二值图像前后各一列
for i = 0:18
    if i<10
        pict(i+1,:)=['00',num2str(i),'.bmp'];
    else
        pict(i+1,:)=['0',num2str(i),'.bmp'];
    end
    a = imread(pict(i+1,:));
    thresh = graythresh(a);
    b = im2bw(a, thresh);
    c = b(:,[1 size(b,2)]);
    X(:,:,i+1)=c;
end
 
subplot(1, 2, 1);
imshow(imtile(pict,'GridSize',[1,19]));
title('原图');
%% III. 计算前后两张图片的Jaccard距离
for i=1:19
    for j=1:19
        if i==j
            d(i,j)=1;
        end
        if i~=j
            m1=0;
            m2=0;
            m0=0;
            for k=1:size(X,1)
                if X(k,size(X,2),i) == X(k,1,j) & X(k,1,j)==1
                    m1=m1+1;
                elseif X(k,size(X,2),i) == X(k,1,j) & X(k,1,j)==0
                    m0=m0+1; 
                else
                    m2=m2+1;
                end
            end
            d(i,j)=m2/(m1+m2+m0);
        end
    end
end
%% IV. 找出第一张和最后一张图片，并找出每张图片的后继
for i=1:19
    [Min,index] = min(d,[],2);
end
f=zeros(1,19);
b=zeros(1,19);
for i=1:19
    front=0;
    behind=0;
    for k=1:size(X,1)
        if X(k,1,i)==1
            front=front+1;
        elseif X(k,size(X,2),i)==1
            behind=behind+1;
        end
    end
    f(1,i)=front;
    b(1,i)=behind;
end
[maxF,indexF] = max(f,[],2);
[maxB,indexB] = max(b,[],2);
%% V. 将图片拼接起来
j=indexF;
for i=1:19
    if j<11
        newpict(i,:)=['00',num2str(j-1),'.bmp'];
    else
        newpict(i,:)=['0',num2str(j-1),'.bmp'];
    end
    j=index(j);
end
subplot(1, 2, 2);
imshow(imtile(newpict,'GridSize',[1,19]));
title('拼接');

2.问题2

（1）聚类结果

1.附件3使用相关距离进行Ward层次聚类结果（无人工干预）

2.附件4使用相关距离进行Ward层次聚类结果（无人工干预）

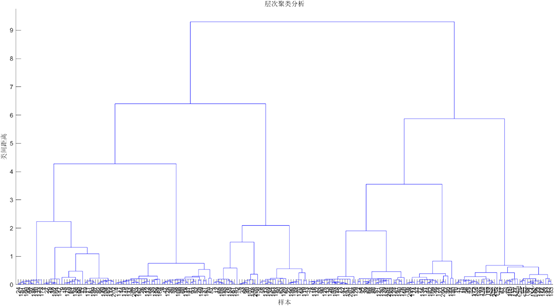
3.附件3使用相关距离进行Ward层次聚类结果（人工干预后）

4.附件4使用相关距离进行Ward层次聚类结果（人工干预后）

（2）拼接复原图
附件3附件4
人工干预前
人工干预后

（3）源码

①Matlab代码

Ⅰ.main.m

%% I. 清空环境
clear
clc
close all
%% II. 导入bmp格式图片，基于阈值将图像转换为二值图像，取二值图像前后各一列
for i = 0:208
    if i<10
        pict(i+1,:)=['00',num2str(i),'.bmp'];
    elseif i<100
        pict(i+1,:)=['0',num2str(i),'.bmp'];
    else
        pict(i+1,:)=[num2str(i),'.bmp'];
    end
    a = imread(pict(i+1,:));
    thresh = graythresh(a);
    b = imbinarize(a, thresh);
    c3 = mean(b,2);
    X(i+1,:)=c3';
end
%% III. 对0-208张图片进行聚类分析
% 样品点之间的距离用相关距离
Y=pdist(X,"correlation");
% 聚类方法用Ward法
z1 = linkage(Y,'ward'); 
clust = 11;  %要聚的类数
c1 = cluster(z1,'maxclust',clust);
for ii = 1:length(clust)
    disp(['分为',num2str(clust(ii)),'类时，每类的频率分布如下：'])
    tabulate(c1(:,ii))  %查看每类的个数
end
%% IV. 将208张图片进行分组
c2=zeros(11,21);
for i = 1:11
    k=1;
    for j = 1:209
        if c1(j,:)==i
            c2(i,k)=j;
            k=k+1;
        end
    end
end
%附件3人工干预
c2(11,18)=c2(9,1);
c2(11,19)=c2(9,11);
temp=2;
for i=1:19
    if(temp==11)
        temp=temp+1;
    end
    c2(9,i)=c2(9,temp);
    temp=temp+1;
end
c2(11,1:end-2)=sort(c2(11,1:end-2) ,'ascend');
c3 = c2(:,[1:end-2]);%所有行 1-倒数第3列
c=c3-1;
%
%附件4人工干预
save c2
%此处进行附件4的人工干预，干预结束后继续
load c2
c = c2;
%
%% V.针对每一组照片，转换为二值图像、计算Jaccard距离以及找出顺序进行拼接
for j = 1:11
    %转换为二值图像
    for i = 0:18
        if(c3(j,i+1)>0)
            if c3(j,i+1)-1<10
                pict2(i+1,:,j)=['00',num2str(c3(j,i+1)-1),'.bmp'];
            elseif c2(j,i+1)-1<100
                pict2(i+1,:,j)=['0',num2str(c3(j,i+1)-1),'.bmp'];
            else
                pict2(i+1,:,j)=[num2str(c3(j,i+1)-1),'.bmp'];
            end
            a = imread(pict2(i+1,:,j));
            thresh = graythresh(a);
            b = im2bw(a, thresh);
            X2(:,:,i+1)=b;
        end
    end
    %计算Jaccard距离、找出顺序
    [d,I]=release(X2,j);
    %由Lingo程序求解出最佳哈密尔顿圈，并保存在INDEX中
    load INDEX
    index=INDEX(j,:)';
    %进行拼接
    for i = 1:19
        realK=c3(j,I);
        if realK<11
            newpict(i,:,j)=['00',num2str(realK-1),'.bmp'];
        elseif realK<101
            newpict(i,:,j)=['0',num2str(realK-1),'.bmp'];
        else
            newpict(i,:,j)=[num2str(realK-1),'.bmp'];
        end
        I=index(I);
    end
    %将拼接好的每大行重新编号保存
    if j<10
        new=['.\new\0',num2str(j),'.bmp'];
    else
        new=['.\new\',num2str(j),'.bmp'];
    end
    imwrite(imtile(newpict(:,:,j),'GridSize',[1 19]),new);
end
%% VI. 将图片显示
subplot(1, 3, 1);
dendrogram(z1);%画图
xlabel('样本')
ylabel('类间距离')
title('层次聚类分析')
subplot(1, 3, 2);
imshow(imtile(pict2,'GridSize',[11 19]));
title('原图');
subplot(1, 3, 3);
imshow(imtile(newpict,'GridSize',[11 19]));
title('拼接');

Ⅱ.release.m

function [d,indexF] = release(X,num)
for i=1:19
    for j=1:19
        if i~=j
            m1=0;
            m2=0;
            m0=0;
            for k=1:size(X,1)
                if X(k,size(X,2),i) == X(k,1,j) & X(k,1,j)==1
                    m1=m1+1;
                elseif X(k,size(X,2),i) == X(k,1,j) & X(k,1,j)==0
                    m0=m0+1; 
                else
                    m2=m2+1;
                end
            end
            d(i,j)=m2/(m0+m1+m2);
        end
    end
end

line=zeros(1,19);
s=zeros(1,size(X,1));
for i=1:19
    s=sum(X(:,:,i));
    for k=1:size(X,1)
        if s(1,k)==size(X,1)
            line(i)=line(i)+1;
        else
            break
        end
    end
end
[maxF,indexF] = max(line,[],2);
%附件4人工干预
if(num==2)
    indexF=19;
end

Ⅲ.horizontal.m(附件4不需要，按自动分类的顺序结果已经基本完成) 在附件3的新建立的new文件夹中进行

%% I. 清空环境
clear
clc
close all
%% II. 导入bmp格式图片，基于阈值将图像转换为二值图像
line=zeros(1,11);
for i = 1:11
    if i<10
        pict=['0',num2str(i),'.bmp'];
    else
        pict=[num2str(i),'.bmp'];
    end
    a = imread(pict);
    thresh = graythresh(a);
    b = im2bw(a, thresh);

    s=zeros(1,size(b,1));
    s=sum(b,2);
    for k=1:size(b,1)
        if s(1,k)==size(b,1)
            line(i)=line(i)+1;
        else
            break
        end
    end

    c = b([1 size(b,1)],:);
    X(:,:,i)=c';
end
%% III. 将图片转置后，计算原上下两张图片的Jaccard距离
for i=1:11
    for j=1:11
        if i==j
            d(i,j)=1;
        end
        if i~=j
            m1=0;
            m2=0;
            m0=0;
            for k=1:size(X,1)
                if X(k,size(X,2),i) == X(k,1,j) & X(k,1,j)==1
                    m1=m1+1;
                elseif X(k,size(X,2),i) == X(k,1,j) & X(k,1,j)==0
                    m0=m0+1; 
                else
                    m2=m2+1;
                end
            end
            d(i,j)=m2/(m1+m2);
        end
    end
end
%% IV. 找出第一张和最后一张图片，并找出每张图片的后继
[maxF,indexF] = max(line,[],2);
%人工干预
indexF=2;
%
index=zeros(11,1);
t=indexF;
for i=1:11
    d(:,t)=1;
    [Min,index(t)]=min(d(t,:),[],2);
    %人工干预
    if t==3
        index(t)=11;
    elseif t==8
        index(t)=10;
    elseif t==10
        index(t)=5;
    end
    %
    t=index(t);
end
%% V. 将图片拼接起来
j=indexF;
for i=1:11
    if j<10
        newpict(i,:,1)=['0',num2str(j),'.bmp'];
    else
        newpict(i,:,1)=[num2str(j),'.bmp'];
    end
    j=index(j);
end
ok=imtile(newpict,'GridSize',[11,1]);
imshow(ok);
title('拼接');
imwrite(ok,'ok.bmp');

②Lingo规划算法求最佳哈密尔顿圈

model:
 
sets:
 
cities/1..19/:u;
 
link(cities,cities):
 
distance,x;endsets
 
data:
 
distance=
!在此输入matlab计算的边权值矩阵
; 
enddata
 
n=@size(cities);
 
min=@sum(link(i,j)|i#ne#j:distance(i,j)*x(i,j));
 
@for(cities(i):
@sum(cities(j)|j#ne#i:x(j,i))=1;
@sum(cities(j)|j#ne#i:x(i,j))=1;
@for(cities(j)|j#gt#1#and#j#ne#i:
u(j)>=u(i)+x(i,j)
-(n-2)*(1-x(i,j))+(n-3)*x(j,i);
);
);
@for(link:@bin(x));
 
@for(cities(i)|i#gt#1:
u(i)<=n-1-(n-2)*x(1,i);
u(i)>=1+(n-2)*x(i,1););
 
end
别之
关注
碎纸片的拼接复原
陌上西风听雨
03-03 5万+
摘  要 对重要文件的拼接复原，传统上都由人工完成，拼接准确率虽然高但是效率很低。本文旨在建立模型，利用计算机编程加少量的人工干预实现碎纸片的拼接复原。 针对问题1，由于对任意一个字符来讲，笔画是连续的，所以对于一般情况，即使文字被切开，两边的像素还是有联系的，是呈现离散性渐变的。针对此特征，建立了文字连续性模型来求解该问题。而又因为被切开的两边碎片边缘灰度是具有高相关性的，所以，又建立了向量
MATLAB碎纸片的自动拼接复原技术
m0_60677550的博客
08-29 3190
MATLAB碎纸片的自动拼接复原技术意义：破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。目前发现对碎纸片的拼接大部分由人工完成，准确率较高，但耗费大量人力财力及时间，效率很低。随着计算机技术的发展，人们试图开发碎纸片的自动拼接技术，以提高拼接复原效率。现先对仅纵切的碎纸片进行研究，开发出利用计算机，更便捷快速拼接碎纸片的方法。背景 碎纸拼接技术及项目背景 ...
基于matlab的碎纸片的拼接复原内含数据集以及说明书.docx
最新发布
05-02
本文档是课题研究的研究报告内含调研以及源码设计以及结果分析
碎纸片的拼接复原MATLAB实现
09-13
通过MATLAB仿真实现规则图片与不规则图片的拼接复原工作。源自--华清
【数学建模】CUMCM-2013B 碎纸片的拼接复原 解题思路整理
bangce8949的博客
09-19 2423
这题看到的反应就是 很好玩 而且答案可以确定正确与否，但是真的没啥实用性（队友：这碎纸片碎的仿佛直接在电脑上用PS处理了一下……） 基本信息 边缘 这是感觉这道题最不符合实际的地方（讲道理）因为边缘信息保留的如此完整……完整到前俩题直接靠这个就能处理掉…… 间距 这个对于中文比较明显（因为这种字体蛮规则的），觉得一张纸...
基于MATLAB的碎纸片拼接复原技术研究
04-20
尤其在图像处理和模式识别方面，MATLAB提供了丰富的函数库和工具箱，这些优势使得MATLAB成为研究和实现碎纸片拼接复原技术的理想选择。 在碎纸片拼接复原技术的实际操作过程中，首先需要进行图像预处理。图像预处理...
基于旅行商规划模型的碎纸片拼接复原问题研究 .zip
05-02
标题中的“基于旅行商规划模型的碎纸片拼接复原问题研究”涉及的是一个将图论中的经典问题——旅行商问题（Traveling Salesman Problem, TSP）应用于实际问题的场景，即碎纸片拼接。在这个研究中，可能探讨了如何...
基于MATLAB碎纸片拼接复原的技术研究.pdf
06-28
整个研究的过程和结果表明，基于MATLAB的碎纸片拼接复原技术具有很强的实用性和效率。这些研究不仅为解决实际问题提供了新思路，也为图像处理领域提供了宝贵的技术参考。对于IT行业特别是图像处理、模式识别和数据...
基于旅行商规划模型的碎纸片拼接复原问题研究.docx
05-02
### 基于旅行商规划模型的碎纸片拼接复原问题研究 #### 概述 本研究探讨了如何运用计算机技术实现碎纸片自动拼接的问题，具体包括三种类型的碎纸片拼接复原问题：RSSTD(Reconstruction of Strip Shredded Text ...
碎纸片的拼接复原算法集合
09-13
碎纸片的拼接复原碎纸片的拼接复原碎纸片的拼接复原
碎纸片拼接
09-13
对碎纸片进行完整的拼接，是Matlab源程序，很有帮助的
碎纸片的拼接复原 MATLAB程序打包
09-13
通过整整8个小时的编程，终于想到了程序的思路了。运用了MATLAB进行仿真，
碎纸片自动拼接复原
08-22
运用聚类算法实现，代码简单易懂，适合新手学习模式识别等课程
基于旅行商模型的文字碎纸片拼接复原-浙江工业大学.rar
11-26
基于旅行商模型的文字碎纸片拼接复原-浙江工业大学，好好加油，相信你的数学建模会学的更好的，好好干，数学建模要多看论文，多看看往年的题目
matlab碎纸拼接相似函数,碎纸片的拼接复原算法及MATLAB实现解析.doc
weixin_28756005的博客
03-21 1129
碎纸片的拼接复原算法及MATLAB实现摘要：对于只有纵切的情形，文章通过比较当前待拼碎片与剩余碎片的信噪比psnr[1,3,4]的值来确定两碎片是否为邻接碎片；拼接算法首先连续调用右拼函数直到拼接到原图右边界，然后连续调用左拼函数直到拼接到原图左边界，从而得到整幅复原图像；对于单面纵横交错切的情形，文章对首先采用纵切拼接算法将碎片拼接成多幅横条图片，然后将各横条图片矩阵转置[2]，再次采用纵切拼接...
MATLAB碎纸片的拼接复原
m0_55395440的博客
08-30 1542
MATLAB碎纸片的拼接复原摘要对于只有纵切的情形，文章通过比较当前待拼碎片与剩余碎片的信噪比psnr[1,3,4]的值来确定两碎片是否为邻接碎片；拼接算法首先连续调用右拼函数直到拼接到原图右边界，然后连续调用左拼函数直到拼接到原图左边界，从而得到整幅复原图像；对于单面纵横交错切的情形，文章对首先采用纵切拼接算法将碎片拼接成多幅横条图片，然后将各横条图片矩阵转置[2]，再次采用纵切拼接算法拼接；两...
MATLAB规则碎纸片拼接
m0_60677550的博客
08-12 852
1、课题意义图像碎片复原技术是一项综合的并具有实用价值的研究课题,它的最终目的是要从大量的任意图像碎片中找出真正符合实际的匹配对,并根据这些匹配关系将相邻的图像碎片拼合起来重现图像的原貌。图像碎片的复原工作是以实际碎片为参考依据进行的,建立能够准确描述实物的计算机模型是图像碎片复原工作的关键步骤之一,对碎片复原的后续工作有基础性的作用,模型建立的准确性和复杂性将影响到后续工作能否顺利进行下去。本文...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值