根据圆的面积公式计算圆周率

圆周率是一个很神奇的数字，看似毫无规律，但却是确确实实存在并且唯一的，圆周率的计算有很多种方法，现在我们假设已知圆的面积公式 $s=\pi r^2$ ,看能不能据此来反推得到 $\pi$ 。

已知条件
- 圆的面积公式： $s=\pi r^2$ ；
- 正六边形是由6个完全相同的等边三角形组成；

所用工具
- 数学推导
- C语言编程

*注意：不能使用三角函数公式计算

推导过程
如图

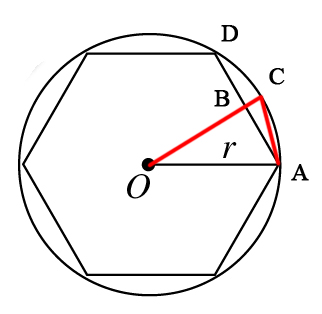
设圆的半径r=1，圆内接 $6*2^n$ 边形的边长为 $a_n$ 。由图可知：

$AC^2=AB^2+BC^2=AB^2+(r-OB)^2=AB^2+(1-\sqrt{1-AB^2})^2$ ,

因此：

• ${a_{n+1}}^2=(a_n/2)^2+(1-\sqrt{1-(a_n/2)^2})^2=\sqrt{2-\sqrt{4-{a_n}^2}}$ ,

至此，我们可以由圆内接正 $6*2^n$ 边形的边长计算得到内接正 $6*2^{n+1}$ 边形的边长。圆的面积可近似看作其内接正多边形的面积，边数越多，近似的结果越准确。

• $s=\pi r^2 \approx s_{n+1}=6*2^{n+1}*（1/2*1*a_n/2)=3a_n*2^n$

因此：

• $\pi=s/r^2=s=3a_n*2^n$ ，

由于 $a_1=1$ 是已知的，便可以联立以上带有项目符号的公式，通过迭代得到 $\pi$ 的估计值。

C代码实现

#include<stdio.h>
#include<math.h>
main()
{
    int n=1;
    double a=1.0,s1=0.0,s2,ds;
    do
    {
        a=sqrt(2-sqrt(4-a*a));
        s2=3*a*pow(2,n);
        ds=s2-s1;
        s1=s2;
        n+=1;
    } while(ds>0.00001);//精确至小数点后第5位
    printf("pi=%f",s1);
}