二叉树面试题
完整代码:
#include <iostream>
using namespace std;
#include <queue>
#include <stack>
template<class T>
//孩子表示法
struct son
{
son(const T& data)
: _left(NULL)
, _right(NULL)
, _data(data)
{}
son<T> *_left;
son<T> *_right;
T _data;
};
template<class T>
//二叉树模版类
class BinaryTree
{
typedef son<T> son;
public:
//无参构造二叉树
BinaryTree()
:_head(NULL)
{}
构造二叉树1
//BinaryTree(const T*array, size_t size, const T& invalid)
//{
// size_t index = 0;
// _head = CreatTree(array, size, invalid, index);
//}
//构造二叉树2
BinaryTree(const T* array, size_t size)
{
size_t index = 0;
CreateBinaryTree(_head, array, size, index);
}
//销毁二叉树
~BinaryTree()
{
ReleaseBinaryTree(_head);
}
//拷贝构造
BinaryTree(const BinaryTree<T> &cp)
{
_head = CopyBinaryTree(cp._head);
}
//赋值
BinaryTree& operator=(const BinaryTree<T> &s)
{
if (this != &s)
{
BinaryTree<T> tmp(s);
swap(_head,tmp._head);
}
return *this;
}
//先序遍历
void Preorder()
{
cout << "先序遍历: ";
PreorderTraversal(_head);
cout << endl;
}
//非递归先序遍历
void PreorderNonRecursive()
{
cout << "非递归先序遍历: ";
PreorderTraversalNonRecursive(_head);
cout << endl;
}
//中序遍历
void Inorder()
{
cout << "中序遍历: ";
InorderTraversal(_head);
cout << endl;
}
//非递归中序遍历
void InorderNonRecursive()
{
cout << "非递归中序遍历: ";
InorderTraversalNonRecursive(_head);
cout << endl;
}
//后序遍历
void Postorder()
{
cout << "后序遍历: ";
PostorderTraversal(_head);
cout << endl;
}
//非递归后序遍历
void PostorderNonRecursive()
{
cout << "非递归后序遍历: ";
PostorderTraversalNonRecursive(_head);
cout << endl;
}
//树的深度
size_t height()
{
return HeightBinaryTree(_head);
}
//叶子结点个数
size_t Leaf()
{
cout << "叶子结点个数: ";
return LeafNode(_head);
}
//广度遍历(层序遍历)
void BreadFirst()
{
cout << "广度遍历: ";
BreadthFirst(_head);
cout << endl;
}
//某一层的结点个数
size_t LayerNode(size_t k)
{
if (height() < k)
return 0;
cout << "第K层的结点个数: ";
return LayerNodes(_head, k);
}
//查找值为data的结点
son* Find(const T&data)
{
return FindNode(_head, data);
}
//查找某个结点的双亲结点
void FindParents(const T&data)
{
son* tmp = Find(data);
son* node = FindNodeParents(_head, tmp);
if (node)
{
cout << "该结点的双亲结点存在,地址为: " << node <<"数据是:"<< node->_data << endl;
}
else
{
cout << "该结点的双亲结点不存在" << endl;
}
}
//结点总数
size_t NodeCount()
{
cout << "结点总数为:";
return GetcountNode(_head);
}
//二叉树镜像
void Image()
{
cout << "二叉树镜像,前序输出:";
BinaryTreeImage(_head);
PreorderTraversal(_head);
cout << endl;
}
//求一棵树是否是完全二叉树
bool Complete()
{
return CompleteBinaryTree(_head);
}
//根据中序和前序重建二叉树
void InPrerebuild(T *preOrder, int startPre, int endPre, T *inOrder, int startIn, int endIn)
{
_head = rebuild(preOrder, startPre, endPre, inOrder, startIn, endIn);
cout << "重建二叉树,前序输出:";
PreorderTraversal(_head);
cout << endl;
}
private:
//构造二叉树2
void CreateBinaryTree(son*& head, const T* array, size_t size, size_t& index)
{
if (array[index] != '#' && index < size)
{
head = new son(array[index]);
CreateBinaryTree(head->_left, array,size,++index);
CreateBinaryTree(head->_right,array,size,++index);
}
}
//构造二叉树1
//son* CreatTree(const T* a, size_t size, const T& invalid, size_t& index)//注意index的传值方式
//{
// son* head = NULL;
// if (a[index] != invalid && index < size)//按先序遍历建树
// {
// head = new son(a[index]);
// head->_left = CreatTree(a, size, invalid, ++index);
// head->_right = CreatTree(a, size, invalid, ++index);
// }
// return head;
//}
//释放二叉树
void ReleaseBinaryTree(son *head)
{
if (head)
{
ReleaseBinaryTree(head->_left);
ReleaseBinaryTree(head->_right);
delete head;
head = NULL;
}
}
//拷贝二叉树
son *CopyBinaryTree(son *head)
{
son *Newhead = NULL;
if (head)
{
Newhead = new son(head->_data);
if (head->_left)
Newhead->_left = CopyBinaryTree(head->_left);
if (head->_right)
Newhead->_right = CopyBinaryTree(head->_right);
}
return Newhead;
}
//先序遍历二叉树
void PreorderTraversal(son *head)
{
if (head)
{
cout <<head->_data <<" ";
PreorderTraversal(head->_left);
PreorderTraversal(head->_right);
}
}
//非递归先序遍历
void PreorderTraversalNonRecursive(son *head)
{
stack<son *> Stack;
if (head == NULL)
{
return;
}
Stack.push(head);
while(!Stack.empty())
{
son *cur = Stack.top();
cout << cur->_data <<" ";
Stack.pop();
if (cur->_right)
Stack.push(cur->_right);
if (cur->_left)
Stack.push(cur->_left);
}
}
//中序遍历
void InorderTraversal(son *head)
{
if (head)
{
InorderTraversal(head->_left);
cout << head->_data << " ";
InorderTraversal(head->_right);
}
}
//非递归中序遍历
void InorderTraversalNonRecursive(son *head)
{
stack<son *> Stack;
if (!head)
{
return;
}
while (head || !Stack.empty())//只要满足一个就执行
{
while (head)
{
Stack.push(head);
head = head->_left;
}
head = Stack.top();
cout << head->_data <<" ";
Stack.pop();
head = head->_right;
}
}
//后序遍历
void PostorderTraversal(son *head)
{
if (head)
{
PostorderTraversal(head->_left);
PostorderTraversal(head->_right);
cout << head->_data <<" ";
}
}
//非递归后序遍历
void PostorderTraversalNonRecursive(son *head)
{
son* cur = head;
son* prev = NULL;//上一个访问过的数据
stack<son*> s;
while (!s.empty() || cur)//只要当前节点和栈不同时为空,就说明树没遍历完
{
//后序遍历,遇到树根节点直接将其压栈
while (cur)
{
s.push(cur);
cur = cur->_left;
}
son* top = s.top();//取栈顶元素,但不一定能访问
//当节点右子树为空或已经访问过时对其直接进行访问
if (top->_right == NULL || top->_right == prev)
{
cout << top->_data << " ";
prev = top;//将prev更新为已经访问的节点
s.pop();
}
else//以子问题的方式去访问右子树
{
cur = top->_right;
}
}
}
//树的深度
size_t HeightBinaryTree(son *head)
{
if (head == NULL)
return 0;
if (head->_left == NULL && head->_right == NULL)
return 1;
size_t LeftHeight = HeightBinaryTree(head->_left);
size_t rightHeight = HeightBinaryTree(head->_right);
return LeftHeight > rightHeight ? LeftHeight + 1 : rightHeight + 1;
}
//叶子节点个数
size_t LeafNode(son *head)
{
if (head == NULL)
return 0;
if (head->_left == NULL && head->_right == NULL)
return 1;
return (LeafNode(head->_left) + LeafNode(head->_right));
}
//广度遍历
void BreadthFirst(son *head)
{
queue<son*> s;
if (head)
{
s.push(head);
}
while (!s.empty())
{
son *tmp = s.front();
s.pop();
cout << tmp->_data << " ";
if (tmp->_left)
s.push(tmp->_left);
if (tmp->_right)
s.push(tmp->_right);
}
}
//第K层的结点个数
size_t LayerNodes(son *head,size_t k)
{
if (head == NULL)
return 0;
if (k == 1)
return 1;
return LayerNodes(head->_left, k - 1) + LayerNodes(head->_right, k - 1);
}
//查找值为data的结点是否存在
son *FindNode(son *head,const T&data)
{
if (head == NULL)
return NULL;
if (head->_data == data)
return head;
son* ret = NULL;
if (ret = FindNode(head->_left, data))
return ret;
return FindNode(head->_right, data);
}
//查找某个结点的双亲结点
son *FindNodeParents(son *head, son *node)
{
if (head == NULL || node == NULL || head == node)
{
return NULL;
}
if (head->_left == node || head->_right == node)
return head;
son* Parents = NULL;
if (Parents = FindNodeParents(head->_left, node))
return Parents;
return FindNodeParents(head->_right, node);
}
//结点总数
size_t GetcountNode(son *head)
{
size_t count = 0;
if (NULL == head)
{
count = 0;
}
else
{
//当前节点 = 左子树节点 + 右子树节点 + 1
count = GetcountNode(head->_left) + GetcountNode(head->_right) + 1;
}
return count;
}
//求一个结点是否在二叉树中
bool IsNodeExist(son *head, son *node)
{
if (node == head)
return ture;
if ((son*tmp = FindNodeParents(head, node)))
{
return true;
}
return false;
}
//二叉树镜像
void BinaryTreeImage(son *head)
{
if (head)
{
swap(head->_left, head->_right);
BinaryTreeImage(head->_left);
BinaryTreeImage(head->_right);
}
}
//求一棵树是否是完全二叉树
bool CompleteBinaryTree(son *head)
{
if (head == NULL)
return true;
queue<son *> s;
s.push(head);
bool flag = false;
while (!s.empty())
{
son *cur = s.front();
if (flag)
{
if (cur->_left || cur->_right)
return false;
}
else
{
if (cur->_left &&cur->_right)
{
s.push(cur->_left);
s.push(cur->_right);
flag = true;
}
else if (cur->_left)
{
s.push(cur->_left);
flag = true;
}
else if (cur->_right)
{
return false;
}
else
flag = true;
}
s.pop();
}
return true;
}
//根据中序和前序重建二叉树
son *rebuild(T *preOrder, int startPre, int endPre, T *inOrder, int startIn, int endIn)
{
//先序遍历和中序遍历长度应相等
if (endPre - startPre != endIn - startIn)
return NULL;
//起始位置不应大于末尾位置
if (startPre > endPre)
return NULL;
//先序遍历的第一个元素为根节点
son *head = new son(preOrder[startPre]);
head->_left = NULL;
head->_right = NULL;
//先序遍历和中序遍历只有一个元素时,返回该节点
if (startPre == endPre)
return head;
//在中序遍历中找到根节点
int index = 0;
int length = 0;
for (index = startIn; index <= endIn; index++)
{
if (inOrder[index] == preOrder[startPre])
break;
}
//若未找到,返回空
if (index > endIn)
return NULL;
//有左子树,递归调用构建左子树
if (index > startIn)
{
length = index - startIn;
head->_left = rebuild(preOrder, startPre + 1, startPre + 1 + length - 1, inOrder, startIn, startIn + length - 1);
}
//有右子树,递归调用构建右子树
if (index < endIn)
{
length = endIn - index;
head->_right = rebuild(preOrder, endPre - length + 1, endPre, inOrder, endIn - length + 1, endIn);
}
return head;
}
private:
son *_head;
};
void Test()
{
//int arr[] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, 6, '#', '#', '#' };
//size_t size = sizeof(arr) / sizeof(arr[0]);
//BinaryTree<int> bt(arr, size,'#');
//BinaryTree<int> bt(arr, size);
char str[] = "ABC##D##E#F##";
size_t size = strlen(str);
BinaryTree<char> bt(str, size);
BinaryTree<char> bt1(bt);
BinaryTree<char> bt2;
bt2 = bt1;
bt.Preorder();
bt.PreorderNonRecursive();
bt1.Inorder();
bt1.InorderNonRecursive();
bt2.Postorder();
bt2.PostorderNonRecursive();
bt2.BreadFirst();
cout << "树的深度: "<< bt2.height() << endl;
cout << bt2.Leaf()<< endl;
cout << bt2.LayerNode(3) << endl;
cout <<bt2.Find('B')<<endl;
bt2.FindParents('B');
cout << bt2.NodeCount() << endl;
bt2.Image();
bt2.Image();
cout << bt2.Complete()<< endl;
char str1[] = "ABCDEF";
char str2[] = "CBDAEF";
bt2.InPrerebuild(str1,0,6,str2,0,6);
}
int main()
{
Test();
system("pause");
return 0;
}
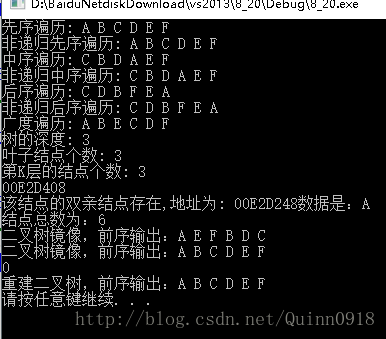
测试结果:
线索化二叉树以及遍历
完整代码:
#include <iostream>
using namespace std;
enum Point{ LINK, THREAD };
template <class T>
struct son
{
son(const T &data)
:_data(data)
,_left(NULL)
,_right(NULL)
, _parent(NULL)
,_leftThread(LINK)
,_rightThread(LINK)
{}
T _data;
son<T> *_left;
son<T> *_right;
son<T> *_parent;
Point _leftThread;
Point _rightThread;
};
template <class T>
class BinaryTreeThd
{
typedef son<T> son;
public:
BinaryTreeThd()
:_head(NULL)
{}
//构造
BinaryTreeThd(const T* array, size_t size)
{
size_t index = 0;
son *parent = NULL;
CreateBinaryTree(_head, array, size, index, parent);
}
//前序线索化
void Prethd()
{
son *prev = NULL;
PreTreethd(_head, prev);
}
//遍历前序线索化
void Preorderthd()
{
cout << "遍历前序线索化: ";
Preorder();
cout << endl;
}
//中序线索化
void Inthd()
{
son *prev = NULL;
InTreethd(_head, prev);
}
//遍历前序线索化
void Inorderthd()
{
cout << "遍历先序线索化: ";
Inorder();
cout << endl;
}
//后序线索化
void Postthd()
{
son *prev = NULL;
PostTreethd(_head, prev);
}
//遍历后序线索化
void Postorderthd()
{
cout << "遍历后序线索化: ";
Postorder();
cout << endl;
}
private:
//构造二叉树
void CreateBinaryTree(son*& head, const T* array, size_t size, size_t& index, son *&parent)
{
if (array[index] != '#' && index < size)
{
head = new son(array[index]);
head->_parent = parent;
CreateBinaryTree(head->_left, array, size, ++index, head);
CreateBinaryTree(head->_right, array, size, ++index, head);
}
}
//前序线索化
void PreTreethd(son *head,son *&prev)
{
if (head)
{
//线索化左指针域
if (NULL == head->_left)
{
head->_left = prev;
head->_leftThread = THREAD;
}
//线索化前一个结点的右指针域
if (prev && NULL == prev->_right)
{
prev->_right = head;
prev->_rightThread = THREAD;
}
prev = head;
if (LINK == head->_leftThread)
PreTreethd(head->_left, prev);
if (LINK == head->_rightThread)
PreTreethd(head->_right, prev);
}
}
//中序线索化
void InTreethd(son *head, son *&prev)
{
if (head)
{
InTreethd(head->_left, prev);
//线索化左指针域
if (NULL == head->_left)
{
head->_left = prev;
head->_leftThread = THREAD;
}
//线索化前一个结点的右指针域
if (prev && NULL == prev->_right)
{
prev->_right = head;
prev->_rightThread = THREAD;
}
prev = head;
if (LINK == head->_rightThread)
InTreethd(head->_right, prev);
}
}
//后序线索化
void PostTreethd(son *head, son *&prev)
{
if (head)
{
PostTreethd(head->_left, prev);
PostTreethd(head->_right, prev);
//线索化左指针域
if (NULL == head->_left)
{
head->_left = prev;
head->_leftThread = THREAD;
}
//线索化前一个结点的右指针域
if (prev && NULL == prev->_right)
{
prev->_right = head;
prev->_rightThread = THREAD;
}
prev = head;
}
}
//遍历前序线索化
void Preorder()
{
son *cur = _head;
while (cur)
{
while (LINK == cur->_leftThread)
{
cout << cur->_data << " ";
cur = cur->_left;
}
cout << cur->_data<< " ";
cur = cur->_right;
访问连在一起的后继
//while (THREAD == cur->_rightThread)
//{
// cur = cur->_right;
// cout << cur->_data << " ";
//}
//if (LINK == cur->_leftThread)
// cur = cur->_left;
//else
// cur = cur->_right;
}
}
//遍历中序线索化
void Inorder()
{
son *cur = _head;
son* prev = NULL;
while (cur)
{
while (LINK == cur->_leftThread)
{
cur = cur->_left;
}
cout << cur->_data << " ";
prev = cur;
while (THREAD == cur->_rightThread)
{
cur = cur->_right;
cout << cur->_data << " ";
prev = cur;
}
cur = cur->_right;
}
}
//遍历后序线索化
void Postorder()
{
son* cur = _head;
son* prev = NULL;
while (cur)
{
//寻找最左节点
while (cur->_left != prev && cur->_leftThread == LINK)
{
cur = cur->_left;
}//cur==_node或NULL结束循环
//访问后继
while (cur && cur->_rightThread == THREAD)//当前节点的右指针为线索
{
cout << cur->_data << " ";
prev = cur;
cur = cur->_right;
}
if (cur == _head)//判断节点是否指向了根节点
{
cout << cur->_data << endl;
return;
}
while (cur && cur->_right == prev)
{
cout << cur->_data << " ";
prev = cur;
cur = cur->_parent;//向上一层走
}
if (cur && cur->_rightThread == LINK)//cur->_rightThread == LINK(当前节点的右指针为子树)
{
cur = cur->_right;
}
}
}
private:
son *_head;
};
void test()
{
char str[] = "ABC##D##E#F##";
size_t size = strlen(str);
BinaryTreeThd<char> bt(str, size);
bt.Prethd();
bt.Preorderthd();
size_t size1 = strlen(str);
BinaryTreeThd<char> bt1(str,size1);
bt1.Inthd();
bt1.Inorderthd();
size_t size2 = strlen(str);
BinaryTreeThd<char> bt2(str,size2);
bt2.Postthd();
bt2.Postorderthd();
}
int main()
{
test();
system("pause");
return 0;
}测试结果:























 345
345

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








