经典算法题总结：回溯，动态规划篇

已于 2024-08-11 15:09:18 修改
阅读量685 收藏 25
点赞数 28
分类专栏： 数据结构与算法 文章标签： 算法 动态规划
于 2024-08-11 14:58:43 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/RQfreefly/article/details/141105764
版权

回溯

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择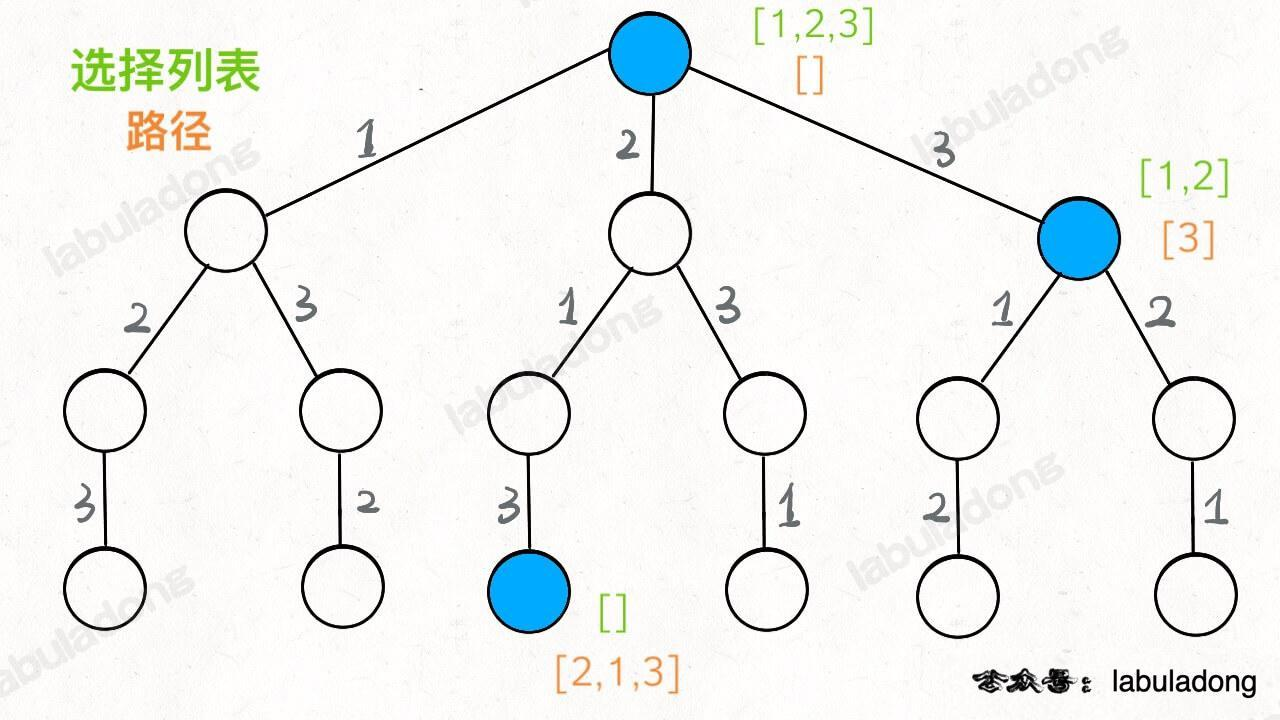

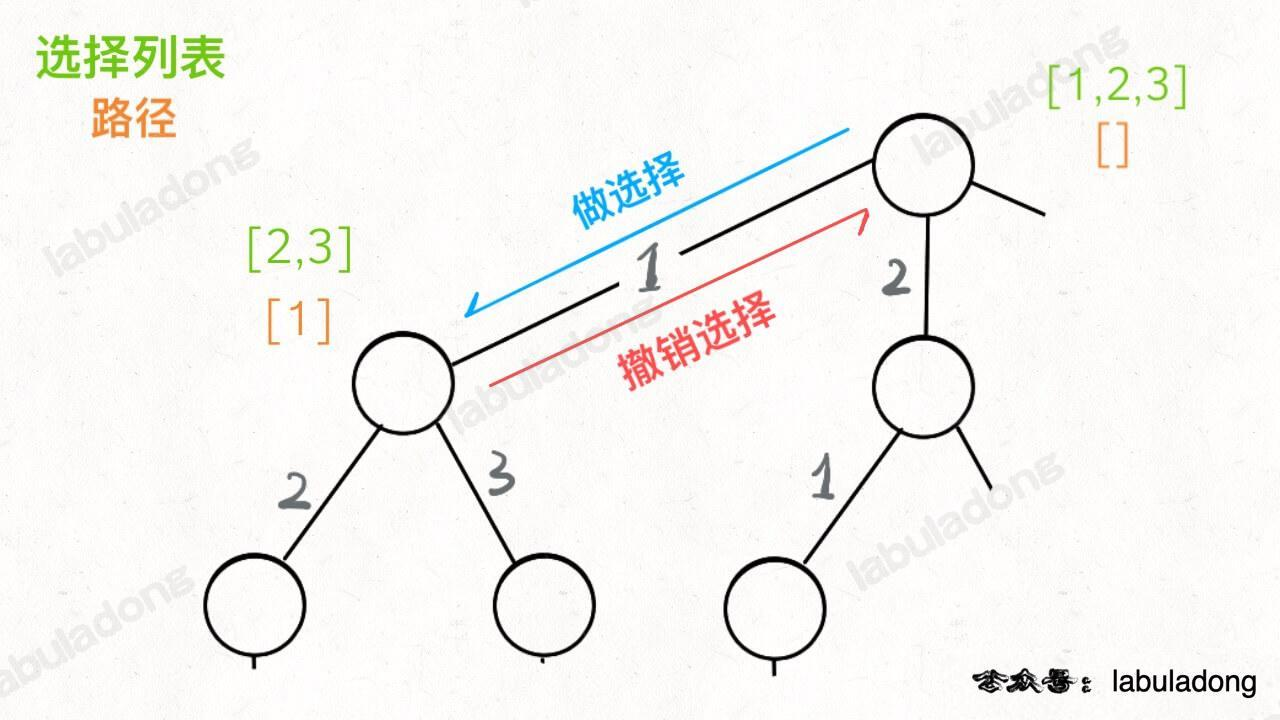
46. 全排列（⭐️⭐️）

思路

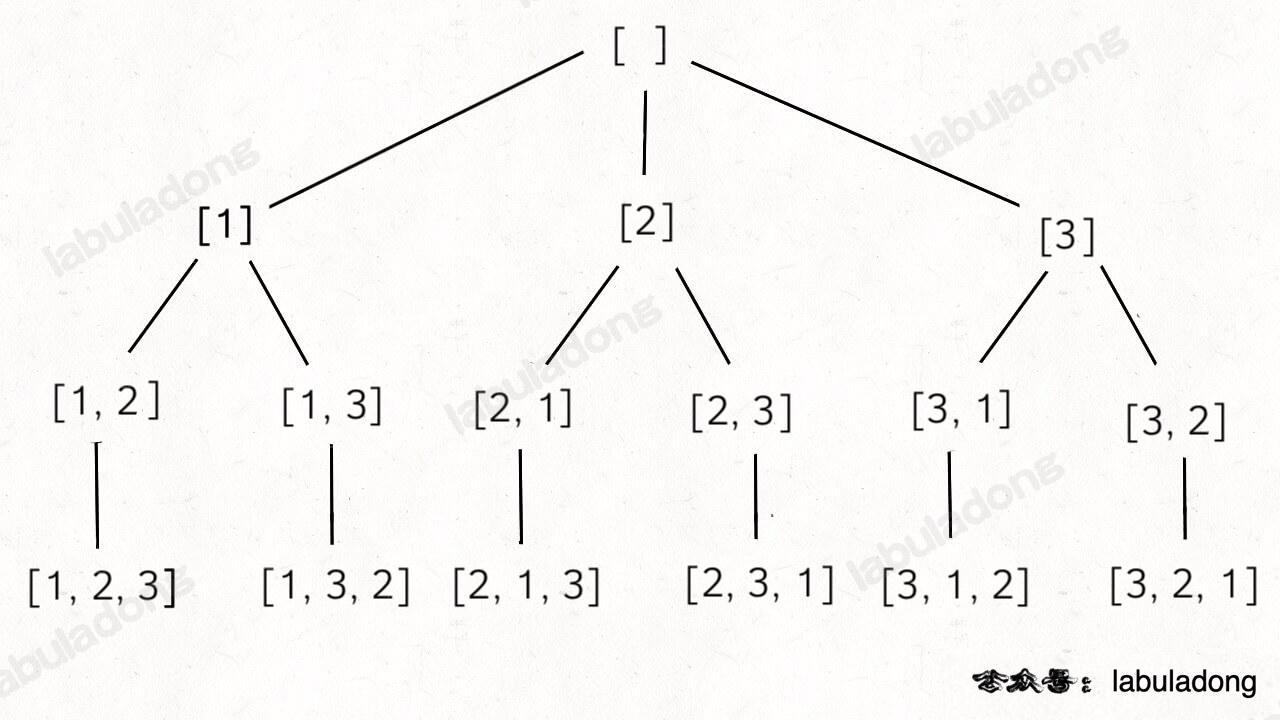
代码

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class Permutations {
    private List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        backtrack(nums, new LinkedList<Integer>(), new boolean[nums.length]);
        return res;
    }
    
    private void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
        if (track.size() == nums.length) {
            res.add(new LinkedList<>(track));
        }
        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            used[i] = true;
            track.add(nums[i]);
            backtrack(nums, track, used);
            track.removeLast();
            used[i] = false;
        }
    }

}

复杂度

93. 复原IP地址（⭐️⭐️）

思路

代码

import java.util.ArrayList;
import java.util.List;

public class RestoreIPAddresses {
    private List<String> res = new ArrayList<>(); // 所有可能的有效 IP 地址
    private List<String> path = new ArrayList<>(); // 临时 IP 地址

    public List<String> restoreIPAddresses(String s) {
        if (s.length() < 4 || s.length() > 12) {
            return res;
        }
        backtrack(s, 0, 0);
        return res;
    }

    /**
     * 回溯复原 IP 地址
     * @param s: 只包含数字的字符串
     * @param splitIndex: 上一段 IP 分割点
     * @param level: 回溯的第几段 IP 地址
     */
    private void backtrack(String s, int splitIndex, int level) {
        if (level > 3) {
            res.add(String.join(".", path));
            return;
        }
        for (int i = splitIndex; i < s.length(); i++) {
            if ((s.length() - i - 1) > 3 * (3 - level)) {
                continue;
            }
            if (!isValidIP(s.substring(splitIndex, i + 1))) {
                continue;
            }
            path.add(s.substring(splitIndex, i + 1));
            backtrack(s, i + 1, level + 1);
            path.remove(path.size() - 1);
        }
    }

    private boolean isValidIP(String s) {
        if (s.charAt(0) == '0' && s.length() > 1) {
            return false;
        }
        if (s.length() > 3) {
            return false;
        }
        if (Integer.parseInt(s) > 255) {
            return false;
        }
        return true;
    }

}

复杂度

22. 括号生成（⭐️⭐️）

思路

代码

import java.util.ArrayList;
import java.util.List;

public class GenerateParentheses {

    public List<String> generateParentheses(int n) {
        List<String> res = new ArrayList<>();
        StringBuilder track = new StringBuilder();
        if (n == 0) {
            return res;
        }
        backtrack(n, n, track, res);
        return res;
    }

    private void backtrack(int left, int right, StringBuilder track, List<String> res) {
        if (right < left) {
            return;
        }
        if (left < 0 || right < 0) {
            return;
        }
        if (left == 0 && right == 0) {
            res.add(track.toString());
            return;
        }
        track.append('(');
        backtrack(left - 1, right, track, res);
        track.deleteCharAt(track.length() - 1);

        track.append(')');
        backtrack(left, right - 1, track, res);
        track.deleteCharAt(track.length() - 1);
    }

}

复杂度

78. 子集（⭐️⭐️）

思路

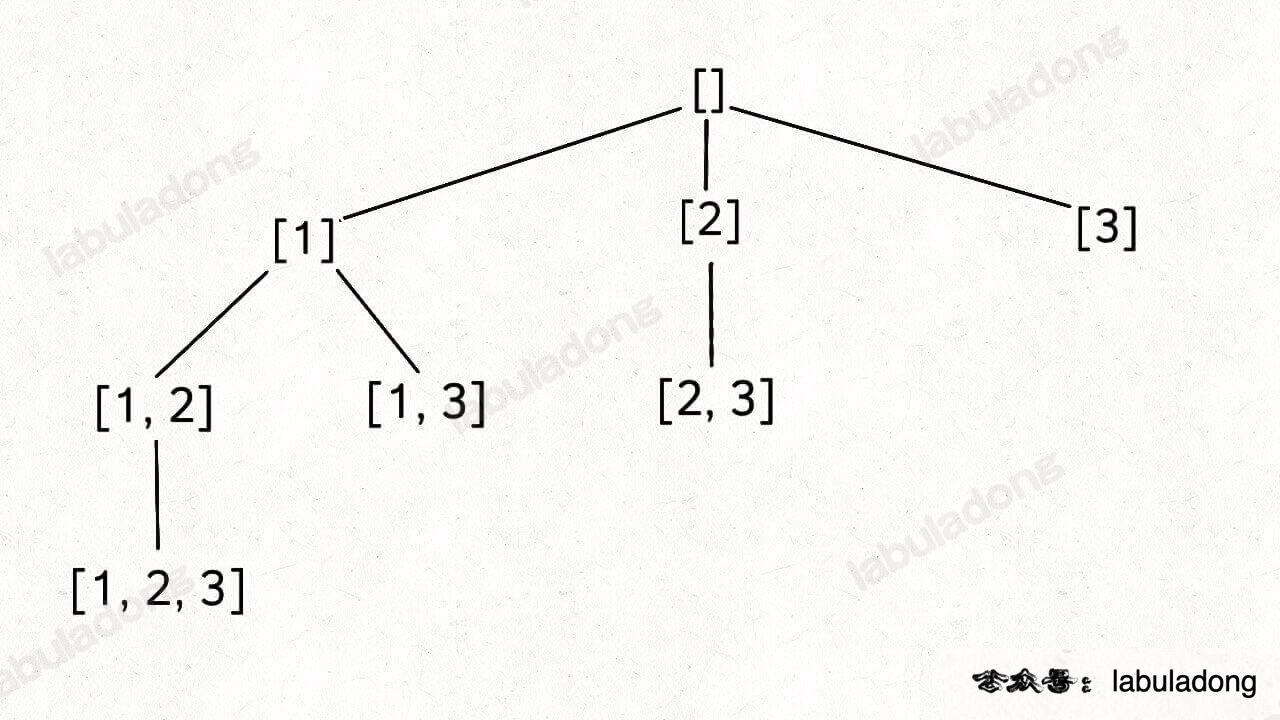
代码

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class Subsets {
    private List<List<Integer>> res = new LinkedList<>();

    public List<List<Integer>> subsets(int[] nums) {
        List<Integer> track = new ArrayList<>();
        backtrack(nums, 0, track);
        return res;
    }

    private void backtrack(int[] nums, int start, List<Integer> track) {
        res.add(new ArrayList<>(track));
        for (int i = start; i < nums.length; i++) {
            track.add(nums[i]); // 做出选择
            backtrack(nums, i + 1, track); // 回溯
            track.remove(track.size() - 1); // 撤销选择
        }
    }

}

复杂度

动态规划

动态规划（Dynamic Programming，简称DP）是一种通过将复杂问题分解为更小的子问题来解决问题的算法设计方法。与分治法类似，动态规划也将问题分解，但不同的是，动态规划适用于那些子问题重叠的情况，即同一子问题会被多次计算。通过记忆化技术（Memoization）或自底向上（Bottom-Up）的方式，动态规划可以显著减少计算量。

动态规划的两个特征：最优子结构，原问题的最优解是从子问题的最优解构建得来的。无后效性，给定一个确定的状态，它的未来发展只与当前状态有关，而与过去经历的所有状态无关。

动态规划的基本思想是：

  1. 将问题分解为子问题：将原问题分解成一系列子问题，并且子问题之间具有重叠性质。
  2. 记忆化或表格法：保存每个子问题的结果，以避免重复计算。这可以通过递归加上记忆化（记忆已经计算过的结果）或通过自底向上填表来实现。
  3. 构造最优解：从已知的子问题结果构造出原问题的解。

动态规划的步骤：

  1. 定义状态：定义一个数组来保存子问题的结果，数组的每个元素表示一个子问题的解。
  2. 设定初始状态：初始化数组的初始状态，即最基本的子问题的解。
  3. 状态转移方程：找到子问题与原问题之间的关系，建立状态转移方程。
  4. 计算最终结果：利用状态转移方程，从初始状态逐步计算，直到得到原问题的解。

首先，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，需要你熟练掌握递归思维，只有列出正确的「状态转移方程」，才能正确地穷举。而且，你需要判断算法问题是否具备「最优子结构」，是否能够通过子问题的最值得到原问题的最值。另外，动态规划问题存在「重叠子问题」，如果暴力穷举的话效率会很低，所以需要你使用「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。

按上面的套路走，最后的解法代码就会是如下的框架：

# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
    for 选择 in 所有可能的选择:
        # 此时的状态已经因为做了选择而改变
        result = 求最值(result, dp(状态1, 状态2, ...))
    return result


# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

53. 最大子数组和（⭐️⭐️）

思路

dp 数组的含义：以 nums[i] 为结尾的「最大子数组和」为 dp[i]。dp[i] 有两种「选择」，要么与前面的相邻子数组连接，形成一个和更大的子数组；要么不与前面的子数组连接，自成一派，自己作为一个子数组。

代码

public class MaxSubArray {

    public int maxSubArray(int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] dp = new int[n];
        dp[0] = nums[0];
        for (int i = 1; i < n; i++) {
            dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
        }
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < n; i++) {
            res = Math.max(res, dp[i]);
        }
        return res;
    }

}

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

70. 爬楼梯（⭐️⭐）

思路

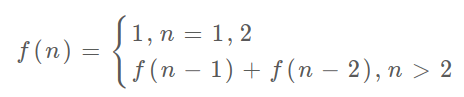
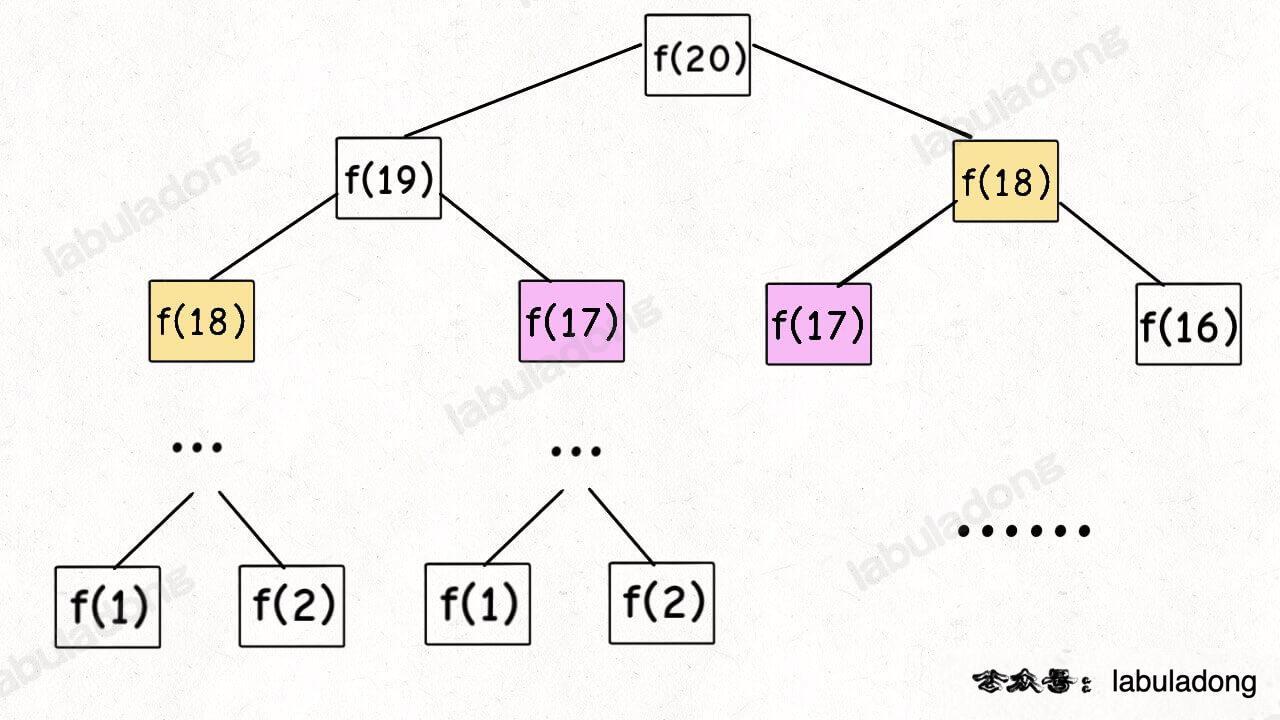
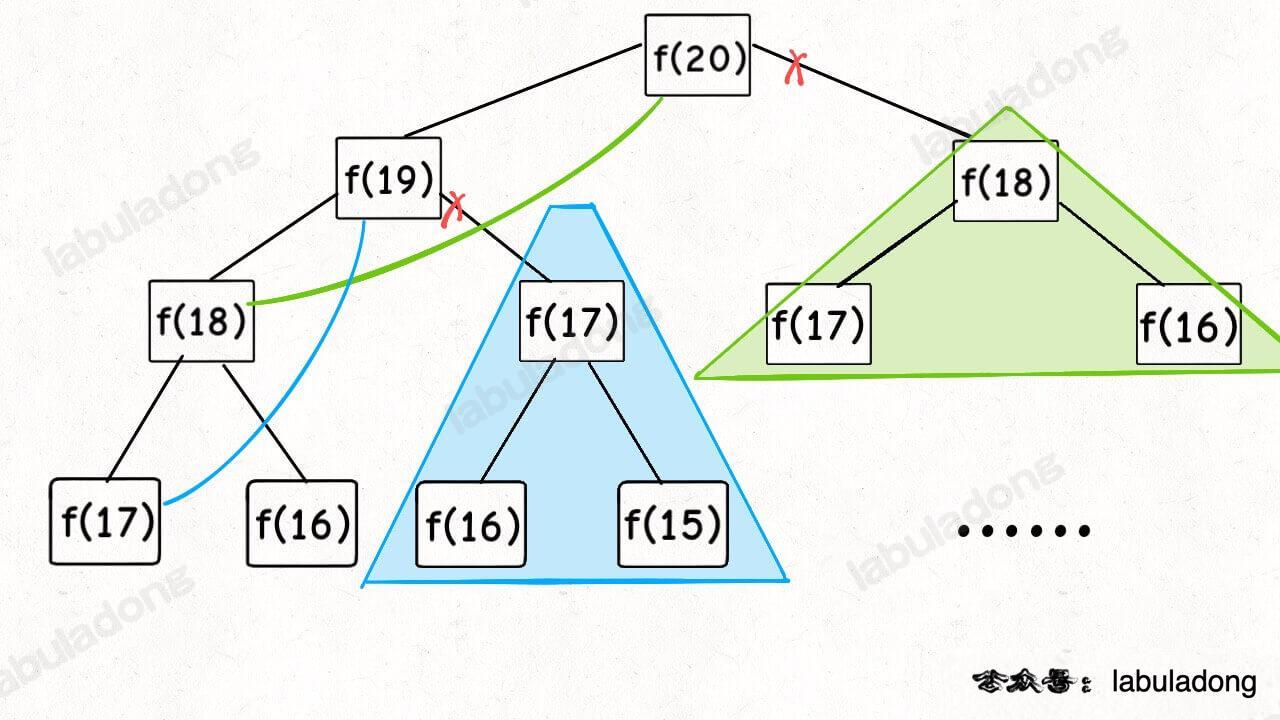
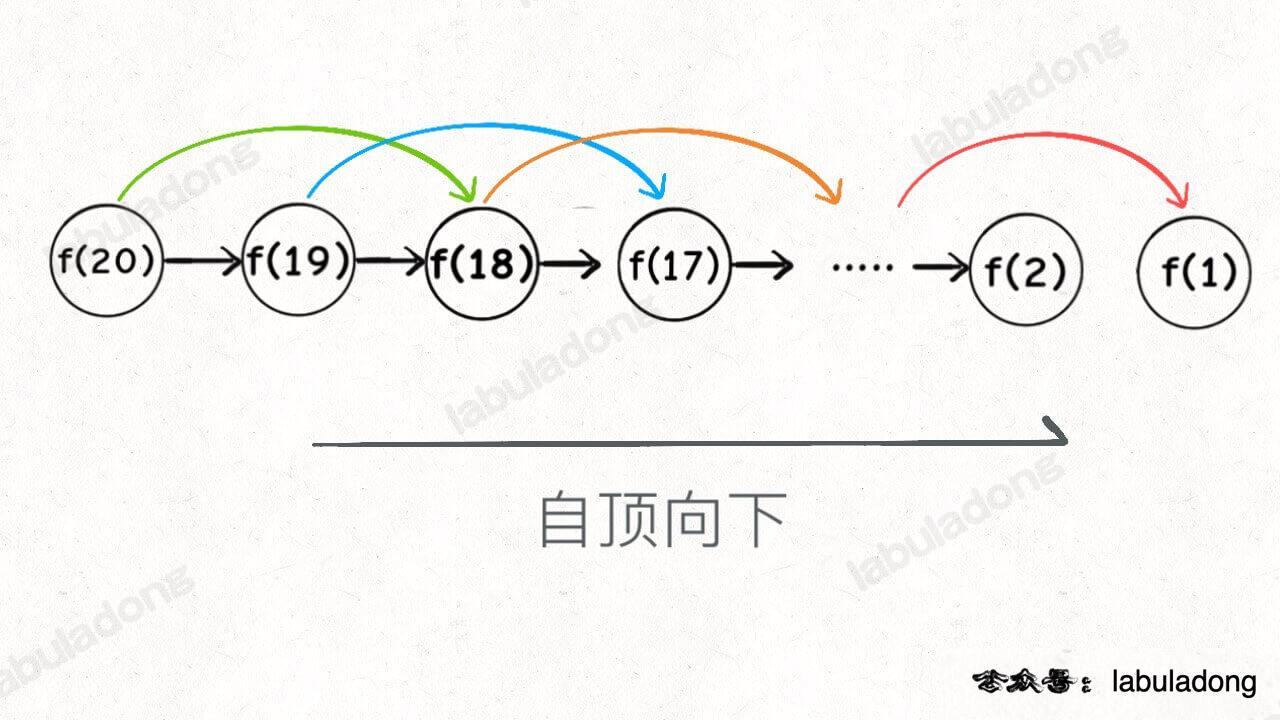
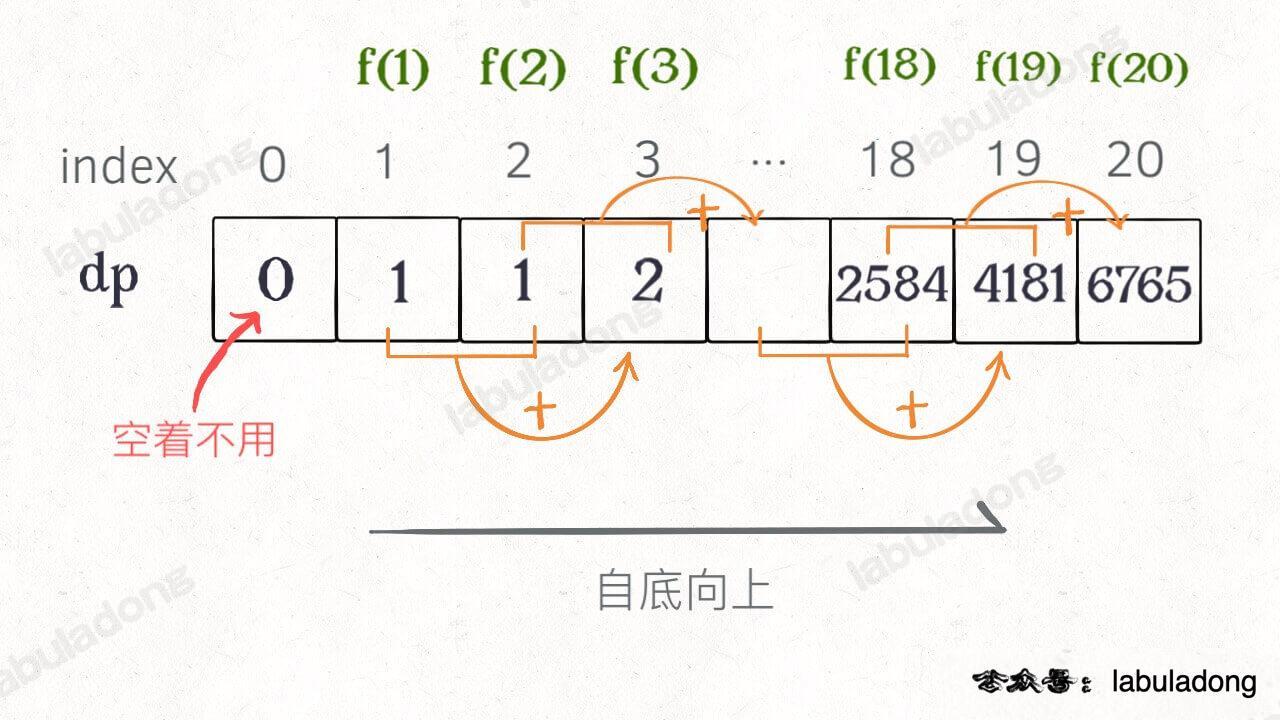
递归 -> 带备忘录的递归 -> 迭代 -> 矩阵快速幂 -> 通项公式。

代码

/**
 * 普通递归解斐波那契数列
 */
public class Fib1 {

    public int fib(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        return fib(n - 1) + fib(n - 2);
    }

}


/**
 * 带备忘录的递归解斐波那契数列
 */
public class Fib2 {

    public int fib(int n) {
        int[] memo = new int[n + 1];
        return dp(memo, n);
    }

    private int dp(int[] memo, int n) {
        if (n == 0 || n == 1) {
            return n;
        }
        if (memo[0] != 0) {
            return memo[n];
        }
        memo[n] = dp(memo, n - 1) + dp(memo, n - 2);
        return memo[n];
    }

}


/**
 * dp 数组的迭代（递推）解斐波那契数列
 */
public class Fib3 {

    public int fib(int n) {
        if (n == 0) {
            return 0;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

}


/**
 * dp 数组的迭代（递推）解斐波那契数列
 */
public class Fib4 {

    public int fib(int n) {
        if (n == 0 || n == 1) {
            return n;
        }
        int dp_i_1 = 1;
        int dp_i_2 = 0;
        for (int i = 2; i <= n; i++) {
            int dp_i = dp_i_1 + dp_i_2;
            dp_i_2 = dp_i_1;
            dp_i_1 = dp_i;
        }
        return dp_i_1;
    }

}

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N) -> O(1)

322. 零钱兑换（⭐️⭐）

思路

1、确定「状态」，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。

2、确定「选择」，也就是导致「状态」产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的「选择」。

3、明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法，所以会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量，也就是上面说到的「状态」；函数的返回值就是题目要求我们计算的量。就本题来说，状态只有一个，即「目标金额」，题目要求我们计算凑出目标金额所需的最少硬币数量。

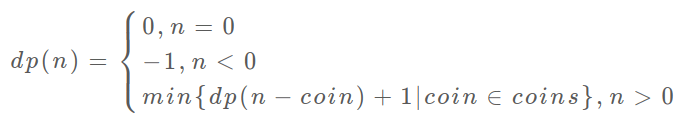
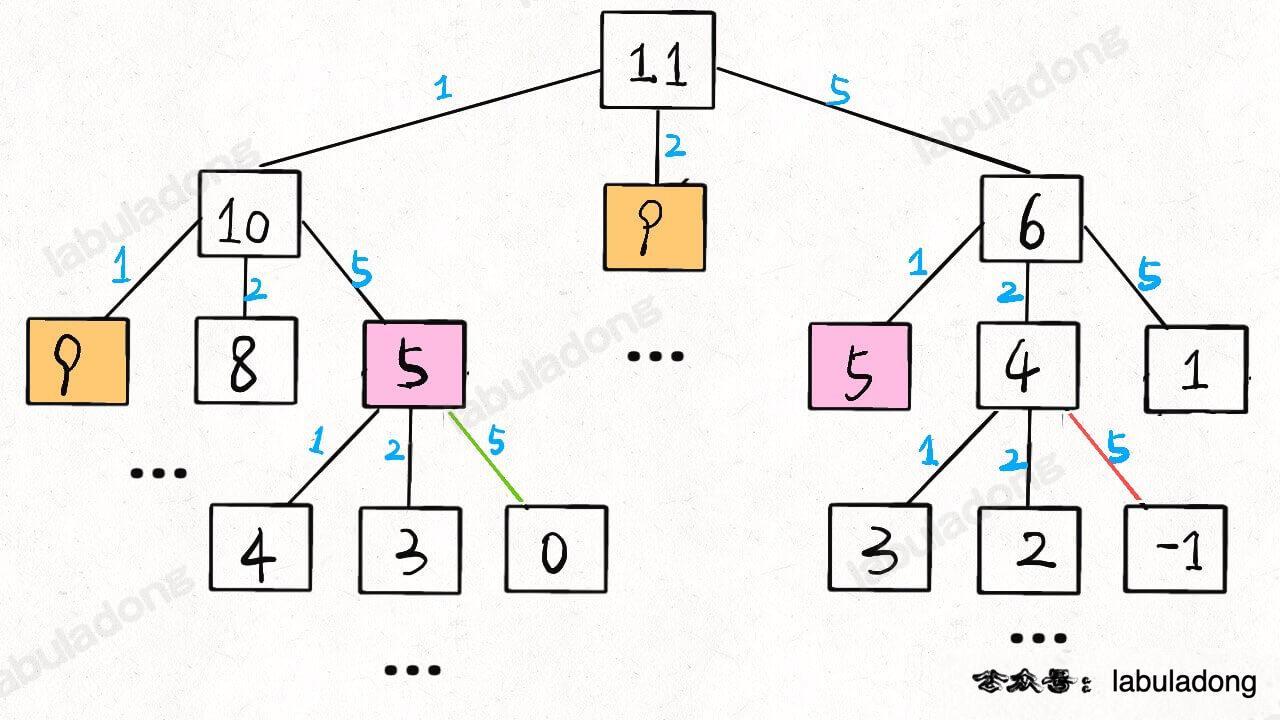
代码

/**
 * 自顶向下进行递归解凑零钱问题
 */
public class CoinChange1 {

    public int coinChange(int[] coins, int amount) {
        return dp(coins, amount);
    }

    private int dp(int[] coins, int amount) {
        if (amount == 0) {
            return 0;
        }
        if (amount < 0) {
            return -1;
        }
        int res = Integer.MIN_VALUE;
        for (int coin : coins) {
            int subProblem = dp(coins, amount - coin); // 子问题最少需要多少硬币
            if (subProblem == -1) {
                continue;
            }
            res = Math.min(res, subProblem + 1);
        }
        return res == Integer.MAX_VALUE ? -1 : res;
    }

}


import java.util.Arrays;

/**
 * 带备忘录的递归解凑零钱问题
 */
public class CoinChange2 {
    private int[] memo;

    public int coinChange(int[] coins, int amount) {
        memo = new int[amount + 1];
        Arrays.fill(memo, Integer.MIN_VALUE);
        return dp(coins, amount);
    }

    private int dp(int[] coins, int amount) {
        if (amount == 0) {
            return 0;
        }
        if (amount < 0) {
            return -1;
        }
        if (memo[amount] != Integer.MIN_VALUE) {
            return memo[amount];
        }
        int res = Integer.MAX_VALUE;
        for (int coin : coins) {
            int subProblem = dp(coins, amount - coin);
            if (subProblem == -1) {
                continue;
            }
            res = Math.min(res, subProblem + 1);
        }
        memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
        return memo[amount];
    }

}


/**
 * dp 数组的迭代解凑零钱问题
 */
import java.util.Arrays;

public class CoinChange3 {

    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        // i 为目标金额
        for (int i = 0; i < dp.length; i++) {
            for (int coin : coins) {
                if (i - coin < 0) {
                    continue;
                }
                dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
            }
        }
        return dp[amount] == Integer.MIN_VALUE ? -1 : dp[amount];
    }

}

复杂度

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)
rongqing2019
关注
  • 28
    点赞
  • 踩
  • 25
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
python 动态规划 回溯_回溯算法和动态规划的转化
weixin_29129919的博客
01-28 410
有的问题如果实在想不出状态转移方程，尝试用回溯算法暴力解决也是一个聪明的策略，总比写不出来解法强。那么，回溯算法和动态规划到底是啥关系？它俩都涉及递归，算法模板看起来还挺像的，都涉及做「选择」，真的酷似父与子。那么，它俩具体有啥区别呢？回溯算法和动态规划之间，是否可能互相转化呢？今天就用力扣第 494 题「目标和」来详细对比一下回溯算法和动态规划，真可谓群魔乱舞：注意，给出的例子 nums 全是 ...
算法｜LeetCode（力扣）经典题：动态规划
峰峰的博客
02-24 2350
LeetCode经典（数据结构与算法）题刷题指南：动态规划篇
算法：回溯算法套路总结
W__winter的博客
05-19 607
算法：回溯算法套路总结
算法-动态规划 Dynamic Programming--从菜鸟到老鸟
热门推荐
有图有真相
07-15 46万+
前言最近在牛客网上做了几套公司的真题，发现有关动态规划（Dynamic Programming）算法的题目很多。相对于我来说，算法里面遇到的问题里面感觉最难的也就是动态规划（Dynamic Programming）算法了，于是花了好长时间，查找了相关的文献和资料准备彻底的理解动态规划（Dynamic Programming）算法。一是帮助自己总结知识点，二是也能够帮助他人更好的理解这个算法。后面的参
回溯算法篇-01：全排列
From_C的博客
01-19 518
力扣46全排列/回溯算法/解题框架
算法设计方法3：动态规划
何哥的博客
03-04 2403
前言：动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。在各大公司的笔试题中，有关动态规划的题目会经常出现。有很多问题，用贪婪法和分治法无法简洁而高效的解决，但是用动态规划就可以。比如0/1背包问题，其中物品不可拆分，使用贪婪法可能不能得到最优解。但是贪心算法适用于可拆分的物品的背包问题，通过性价比排名就可以进......
【继动态规划后&计划】回溯算法和动态规划的区别与转换
少年初心的博客
03-12 1724
动态规划几篇文章已经完成，接下来看 优势、什么时候用…… 我们前文经常说回溯算法和递归算法有点类似，有的问题如果实在想不出状态转移方程，尝试用回溯算法暴力解决也是一个聪明的策略，总比写不出来解法强。 那么，回溯算法和动态规划到底是啥关系？它俩都涉及递归，算法模板看起来还挺像的，都涉及做「选择」，真的酷似父与子。 那么，它俩具体有啥区别呢？回溯算法和动态规划之间，是否可能互相转化呢？ 今天就用力扣第 494 题「目标和」来详细对比一下回溯算法和动态规划，真可谓群魔乱舞： 注意，给出的例子 nums .
回溯算法总结篇
passport404的博客
12-07 796
定义 首先先来了解一下回溯的定义吧 回溯是递归的副产物，只要有递归就会有回溯 所以回溯经常和二叉树，深度优先遍历等操作联系到一起，因为他们都用到了递归。 回溯本质上是暴力搜索，效率并不高，最多剪枝一下。 回溯法可以解决的问题 组合问题：N个数里面按一定规则找出k个数的集合 排列问题：N个数按一定规则全排列，有几种排列方式 切割问题：一个字符串按一定规则有几种切割方式 子集问题：一个N个数的集合里有多少符合条件的子集 棋盘问题：N皇后，解数独等等 回溯模板（重点） void backtracking(
【算法刷题】动态规划算法题型及方法归纳
STAR GAME
02-25 2065
动态规划中每一个状态一定是由上一个出来，根据这个特点，可以在过程中，存储某一条件下的数据，当再次遍历该条件时，直接取该条件对应的数据即可，可以避免重复计算，减少时间。
面试高频算法题总结，个人博客
05-29
本篇文章将对一些常见的面试算法题目进行总结，重点讨论Python语言下的实现方式。 一、排序算法 1. 冒泡排序：基础排序算法，通过不断交换相邻的逆序元素来完成排序。Python实现简洁易懂，但效率较低。 2. 快速...
leetcode题库-LeetCode:算法
06-29
LeetCode提供的题目覆盖了排序、搜索、图论、动态规划等多个领域，是提升算法能力的理想平台。 在LeetCode上，你可以遇到诸如二分查找、回溯法、贪心策略、深度优先搜索（DFS）和广度优先搜索（BFS）等经典算法。...
Algorithm:个人算法刷题总结，利用JS语言，每道题尝试优化最优解或最简洁的方法
03-20
本篇将主要围绕“个人算法刷题总结”，聚焦JavaScript语言，探讨如何通过优化实现算法的最优解和最简洁的方法。 首先，算法是解决问题的步骤和方法，是计算机科学的基础。JS（JavaScript）作为一种广泛使用的脚本...
算法设计与分析-以ACM大学生程序设计竞赛在线题库为例
11-28
- **动态规划**：一种通过将问题分解为子问题来求解的方法，适用于求解具有重叠子问题性质的问题。 #### ACM竞赛中的算法应用 ACM竞赛题目通常围绕着具体的场景或问题展开，需要参赛者灵活运用各种算法知识来解决...
leetcode:leetcode算法
05-10
1. 动态规划：动态规划是一种解决最优化问题的常用方法，例如斐波那契数列、背包问题等。Java中，可以利用二维数组来存储子问题的解，逐步构建出全局最优解。 2. 回溯法：回溯法常用于解决组合优化问题，如八皇后...
备战秋招60天算法挑战，Day17
最新发布
溜达虎的博客
08-13 188
给定两个字符串 和 ，编写一个函数来判断 是否是 的字母异位词。注意： 若 和 中每个字符出现的次数都相同，则称 和 互为字母异位词。举个例子： 视频题解 有效的字母异位词 思路来源 思路来源 思路解析 方法一 排序 分别对和进行排序，然后比较排序后的字符串是否相等。 java代码 python代码 复杂度分析 时间复杂度： 快排的时间复杂度是O(nlogn)，其中是字符串的长度。空间复杂度： 快排的空间复杂度是O(logn)。假设， 。 java代码 python代码 复杂度分析 时
day 9 回溯算法
m0_73924943的博客
08-08 363
优化后的比之前的在叶子结点少递归一层。在排序candidates后，碰到target<0的情况直接结束本层的遍历，后面没遍历到的也不用遍历了。1.目标数n一直在随i的加入减小，如果目标数n已经<0，那么剪枝。即path中的数已经大于目标数了。利用数组去重，因为题目的数值范围小，所以可以尽量使用。剪枝优化：（对每层循环遍历的范围进行了缩小）2.对for循环i的遍历范围进行缩小。也可以不用st数组去重。
代码随想录算法训练营第十一天
b1ankwall的博客
08-10 1196
参加代码随想录第43期算法训练营day11|150. 逆波兰表达式求值，239. 滑动窗口最大值，347.前 K 个高频元素，栈与队列总结
[算法2] 第二集 二叉树中的深度搜索
2301_80017277的博客
08-09 853
一、（DFS，全称为 Depth First Traversal），是我们树或者图这样的数据结构中常⽤的⼀种遍历算法。这个算法会尽可能深的搜索树或者图的分支，直到⼀条路径上的所有节点都被遍历完毕，然后再回溯到上⼀层，继续找⼀条路遍历。在⼆叉树中，常见的深度优先遍历为：前序遍历、中序遍历以及后序遍历。因为树的定义本⾝就是递归定义，因此采⽤递归的方法去实现树的三种遍历不仅容易理解⽽且代码很简洁。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值