# 1987年的那件神秘的往事

1987年的那件神秘的往事

1.前言

在1987年发生了一件令当年的研究生考试的考生都难以忘怀的事情。当年的数学卷子出现了如下的一道题目。

1987 考研
设两箱内装有同种零件，第一箱装50件，其中有10 件一等品，
第二箱装30件，其中有18件一等品，先从两箱中任挑一箱，
再从此箱中前后不放回任取两个零件，求：
		（1）先取出的零件是一等品的概率p．
		（2）在先取出的是一等品的条件下，后取的仍是一等品的条件概率q．

此题一度被认为是“颇具争议”。其中第二问，命题人王式安和考研老师张宇分别给出了两种解法。本文中我们将介绍这两种解法，并用计算机模拟的方式来检验计算这道题目。

2.两种解法

讨论第二问之前我们先解决第一问。十分明显这是一个全概率的问题
$$p=\frac{1}{2}\times \frac{10}{50}+\frac{1}{2}\times \frac{18}{30}=0.4$$
对于第一问两位老师没有疑义，但在第二问上发生了分歧。

1）王式安解法

传说王式安的求解结果是0.385，根据我的的推测，王老师的做法应该是用的全概率公式
$$p=\frac{1}{2}\times \frac{9}{49}+\frac{1}{2}\times \frac{17}{29}=0.385$$
可以推测，王老师认为，由条件可知第一个零件为正品，由此套全概率公式计算第二个零件为正品的概率。

2）张勇解法

张勇老师使用了条件概率公式，设事件A为第一个为正品，事件B为第二个为正品
$$p(B|A)=\frac{p(AB)}{p(A)}=\frac{\frac{1}{2}\times \frac{10}{50}\times \frac{9}{49}+\frac{1}{2}\times \frac{18}{30}\times \frac{17}{29}}{0.4}=0.4855$$

3.程序模拟

众所周知，java是我国人民擅长的编程语言，因此我们选择java作为本次模拟的编程语言。
首先我们构建一个盒子类用来辅助计算。

class Box{
    private boolean [] box;
    private int effectiveLength;
    public Box(int totalSize, int positiveNum){
        assert totalSize >= positiveNum;
        effectiveLength = totalSize;
        box = new boolean[totalSize];
        for (int i = 0; i < positiveNum; i++){
            int index = (int) (Math.random() * totalSize);
            while (box[index]){
                index = (int) (Math.random() * totalSize);
            }
            box[index] = true;
        }
    }
    public boolean fetchOne(){
        assert effectiveLength > 0;
        //选择取的下标
        int index = (int) (Math.random() * effectiveLength);
        //交换取的位置与最后一个位置
        boolean temp = box[index];
        box[index] = box[effectiveLength - 1];
        box[effectiveLength - 1] = temp;
        //有效位前移
        effectiveLength --;
        return box[effectiveLength];
    }
}

Box的构造函数接受总零件数和正品数，生成一个布尔数组，中true代表正品，false代表非正品。构造函数可以使得其中的正品和次品是分散交错的，而非正品和次品连续排布。我们可以从数学上证明，尽管生成的for循环中嵌套了while循环，但可以在很高的概率上保证这个for循环可以在多项式时间甚至是亚线性时间内完成。
其次为了保证模拟取出不放回，我们为Box类添加一个fetchOne()方法，该方法可以随机取出一个零件，并将该零件“删除”。事实上这是一种很经典的删除策略：为了保证删除后的其他零件是连续的，我们将选定的零件置换到数组末端，再将其删除。
java中提供了类似C++的vector类，但我还不太会用，就姑且用有效位来标记未被取出的连续零件。

下面我们开始试验，我们统计在条件“第一个为正品”成立的情况下，第二件也为正品的频率。

public static void main(String[] args) {
    long labCounter = 0; //总试验次数
    long conditionEstablishedCounter = 0; //条件成立次数
    long secondPositivePartCounter = 0; //第二件正品次数
    while (labCounter < 1000000){
        //初始化两个箱子
        Box box1 = new Box(50, 10);
        Box box2 = new Box(30, 18);
        //选一个箱子，使用随机数
        double randomNumber = Math.random();
        Box b = randomNumber > 0.5 ? box1:box2;
        //抽第一个零件
        boolean firstPart = b.fetchOne();
        //抽第二个零件
        boolean secondPart = b.fetchOne();

        labCounter ++;
        if (firstPart){
            conditionEstablishedCounter ++;
            if (secondPart){
                secondPositivePartCounter ++;
            }
        }
        if (labCounter % 10000 == 0 || labCounter < 100 && labCounter % 10 == 0){
             System.out.println("total：" + labCounter + ", condition established total：" + conditionEstablishedCounter + ", second positive total："
                + secondPositivePartCounter + "，total frequency：" + (double) secondPositivePartCounter / conditionEstablishedCounter);

        }
    }
}

在每次试验前，我们初始化题目中的两个箱子，并以二分之一的概率随机选一个，再进行两次取操作。总共进行一亿次试验，统计其频率。第一亿的输出如下

total：100000000, condition established total：40004508, 
second positive total：19422209，
total frequency：0.48550050909262527

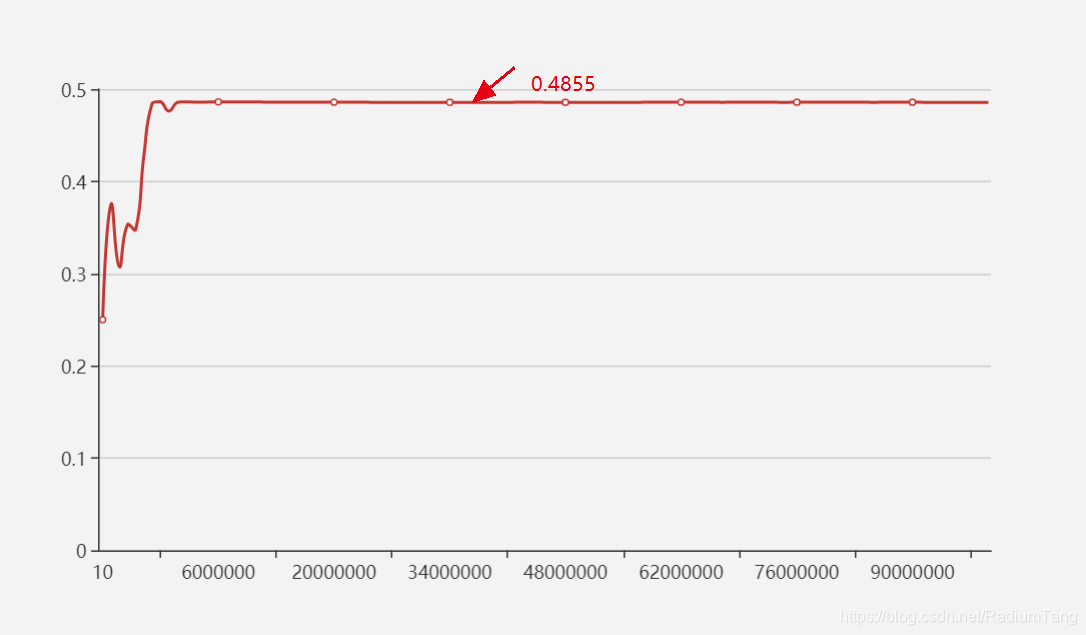
可以看到在一百万次实验中，第一次抽出正品，即条件成立出现了40，004，508次，在第一次抽出正品时，第二次抽出正品发生了19，422，209次，其频率非常接近0.4855。(横坐标为试验次数，纵坐标为频率）

4.经验解释

至此，我们可以基本断定，张勇老师的解法有较大可能是正确的。事实上，在考研的复习全书上有一道类似的题目

1987 考研
设两箱内装有同种零件，第一箱装n件，其中有n 件一等品，
第二箱装m件，其中有1件一等品，先从两箱中任挑一箱，
再从此箱中前后不放回任取两个零件，求：
		（1）先取出的零件是一等品的概率p．
		（2）在先取出的是一等品的条件下，后取的仍是一等品的条件概率q．

按照上述张宇和王式安的解法分别求解第二问，得到的结果分别是
$\frac{m}{m+1}$ 和 $\frac{1}{2}$，显然第一个结果看起来更加正确，因为根据经验，当条件发生时，我们有更大把握抽的是第一个箱子。
更极端地，我们考虑第二个箱子的m趋向于正无穷，此时从第二个箱子中抽出正品的概率为0，因此当条件成立时，说明我们抽的是第一个箱子，因此第二件为正品的概率趋向于1，而非1/2。

然而，复习全书上赫然写着的答案竟然是1/2，甚至将另一种做法标记为错误解法，加以批评（见数学考研复习全书445页）

5.实验理论

这一部分本应放在实验之前，但我们懒得做严格的证明，仅在此说明。

1）计算机随机数

大部分计算机的随机数生成与程序运行时间或随机数种子有关。对于程序运行时间相关的随机数，我们可以证明，其运行时间随机选择某一时刻得到的微秒数，其个位数字分布必定为均匀分布。更进一步的，我们可以证明这个微秒数对任一较小整数求模，得到的结果也是均匀分布 。

2）程序模拟随机性

在生成箱子的构造函数中，我们可以让正品和次品交错分布，在取件方法中，我们可以保证取出的零件是随机的，每个零件被取出的概率是相等的

3）频率逼近概率

有许多定理告诉我们，当实验足够多的时，频率应该接近于概率。因此我们有极大的把握断定，张宇老师的解法应该是正确的。

6.尾声

在第一次在全书上看到这个题目的时候，我也采用了王式安老师的解法。这主要是由于我概念不清、麻痹大意导致的，在考研复习阶段，我们应该努力避免这种情况的发生。一般认为，避免此类情况的途径有两种：

1）努力学习，认真看书，搞清概念，熟悉题型

2）设法避免考研