BP神经网络
符号及其含义
- n l n_l nl表示第 l l l层神经元的个数;
- f ( ⋅ ) f(·) f(⋅)表示神经元的激活函数;
- W ( l ) ∈ R n i ∗ n i − 1 W^{(l)}\in\mathbb R^{n_i*n_{i-1}} W(l)∈Rni∗ni−1表示第 l − 1 l-1 l−1层到第 l l l层的权重矩阵;
- w i j ( l ) w_{ij}^{(l)} wij(l)是权重矩阵 W ( l ) W^{(l)} W(l)中的元素,表示第 l − 1 l-1 l−1层第 j j j个神经元到第 l l l层第 i i i个神经元的连接的权重(注意标号的顺序);
- b ( l ) = ( b 1 ( l ) , b 2 ( l ) , . . . , b n l ( l ) ) T ∈ R ( n l ) b^{(l)}=(b_1^{(l)},b_2^{(l)},...,b_{nl}^{(l)})^T\in\mathbb R^{(nl)} b(l)=(b1(l),b2(l),...,bnl(l))T∈R(nl)表示 l − 1 l-1 l−1层到第 l l l层的偏置;
- z ( l ) = ( z 1 ( l ) , z 2 ( l ) , . . . , z n l ( l ) ) T ∈ R ( n l ) z^{(l)}=(z_1^{(l)},z_2^{(l)},...,z_{nl}^{(l)})^T\in\mathbb R^{(nl)} z(l)=(z1(l),z2(l),...,znl(l))T∈R(nl)表示 l l l层神经元的状态;
- a ( l ) = ( a 1 ( l ) , a 2 ( l ) , . . . , a n l ( l ) ) T ∈ R ( n l ) a^{(l)}=(a_1^{(l)},a_2^{(l)},...,a_{nl}^{(l)})^T\in\mathbb R^{(nl)} a(l)=(a1(l),a2(l),...,anl(l))T∈R(nl)表示 l l l层神经元的激活值(即输出值)。

图
1
图1
图1
显然,图1所示神经网络的第2层神经元的状态及激活值可以通过下面的计算得到:
z
1
(
2
)
=
w
11
(
2
)
x
1
+
w
12
(
2
)
x
2
+
w
13
(
2
)
x
3
+
b
1
(
2
)
z_1^{(2)}=w_{11}^{(2)}x_1+w_{12}^{(2)}x_2+w_{13}^{(2)}x_3+b_1^{(2)}
z1(2)=w11(2)x1+w12(2)x2+w13(2)x3+b1(2)
z
2
(
2
)
=
w
21
(
2
)
x
1
+
w
22
(
2
)
x
2
+
w
23
(
2
)
x
3
+
b
2
(
2
)
z_2^{(2)}=w_{21}^{(2)}x_1+w_{22}^{(2)}x_2+w_{23}^{(2)}x_3+b_2^{(2)}
z2(2)=w21(2)x1+w22(2)x2+w23(2)x3+b2(2)
z
3
(
2
)
=
w
31
(
2
)
x
1
+
w
32
(
2
)
x
2
+
w
33
(
2
)
x
3
+
b
3
(
2
)
z_3^{(2)}=w_{31}^{(2)}x_1+w_{32}^{(2)}x_2+w_{33}^{(2)}x_3+b_3^{(2)}
z3(2)=w31(2)x1+w32(2)x2+w33(2)x3+b3(2)
a
1
(
2
)
=
f
(
z
1
(
2
)
)
a_1^{(2)}=f(z_1^{(2)})
a1(2)=f(z1(2))
a
2
(
2
)
=
f
(
z
2
(
2
)
)
a_2^{(2)}=f(z_2^{(2)})
a2(2)=f(z2(2))
a
3
(
2
)
=
f
(
z
3
(
2
)
)
a_3^{(2)}=f(z_3^{(2)})
a3(2)=f(z3(2))
(
1
)
(1)
(1)
类似地,第3层神经元的状态及激活值可以通过下面的计算得到:
z
1
(
3
)
=
w
11
(
3
)
a
1
(
2
)
+
w
12
(
3
)
a
2
(
2
)
+
w
13
(
3
)
a
3
(
2
)
+
b
1
(
3
)
z_1^{(3)}=w_{11}^{(3)}a_1^{(2)}+w_{12}^{(3)}a_2^{(2)}+w_{13}^{(3)}a_3^{(2)}+b_1^{(3)}
z1(3)=w11(3)a1(2)+w12(3)a2(2)+w13(3)a3(2)+b1(3)
z
2
(
3
)
=
w
21
(
3
)
a
1
(
2
)
+
w
22
(
3
)
a
2
(
2
)
+
w
23
(
3
)
a
3
(
2
)
+
b
2
(
3
)
z_2^{(3)}=w_{21}^{(3)}a_1^{(2)}+w_{22}^{(3)}a_2^{(2)}+w_{23}^{(3)}a_3^{(2)}+b_2^{(3)}
z2(3)=w21(3)a1(2)+w22(3)a2(2)+w23(3)a3(2)+b2(3)
a
1
(
3
)
=
f
(
z
1
(
3
)
)
a_1^{(3)}=f(z_1^{(3)})
a1(3)=f(z1(3))
a
2
(
3
)
=
f
(
z
2
(
3
)
)
a_2^{(3)}=f(z_2^{(3)})
a2(3)=f(z2(3))
(
2
)
(2)
(2)
可总结出,第
l
(
2
<
=
l
<
=
L
)
l(2<=l<=L)
l(2<=l<=L)层神经元的状态及激活值为(下面式子是向量表示形式):
z
(
l
)
=
W
(
l
)
a
(
l
−
1
)
+
b
(
l
)
(
3
)
z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}\\(3)
z(l)=W(l)a(l−1)+b(l)(3)
对于训练的数据集,使用均方误差作为损失函数来评估整体误差:
E
r
r
o
r
=
1
2
[
(
y
1
−
a
1
(
3
)
)
2
+
(
y
2
−
a
2
(
3
)
)
2
]
Error=\frac{1}{2}\begin{bmatrix} (y_1-a_1^{(3)})^2+(y_2-a_2^{(3)})^2 \end{bmatrix}
Error=21[(y1−a1(3))2+(y2−a2(3))2]
(
4
)
(4)
(4)
把
E
E
E展开到隐藏层:
E
=
1
2
[
(
y
1
−
a
1
(
3
)
)
2
+
(
y
2
−
a
2
(
3
)
)
2
]
E=\frac{1}{2}\begin{bmatrix} (y_1-a_1^{(3)})^2+(y_2-a_2^{(3)})^2 \end{bmatrix}
E=21[(y1−a1(3))2+(y2−a2(3))2]
E
=
1
2
[
(
y
1
−
f
(
z
1
(
3
)
)
)
2
+
(
y
2
−
f
(
z
2
(
3
)
)
)
2
]
E=\frac{1}{2}\begin{bmatrix} (y_1-f(z_1^{(3)}))^2+(y_2-f(z_2^{(3)}))^2 \end{bmatrix}
E=21[(y1−f(z1(3)))2+(y2−f(z2(3)))2]
E
=
1
2
[
(
y
1
−
f
(
w
11
(
3
)
a
1
(
2
)
+
w
12
(
3
)
a
2
(
2
)
+
w
13
(
3
)
a
3
(
2
)
+
b
1
(
3
)
)
)
2
+
(
y
2
−
f
(
w
21
(
3
)
a
1
(
2
)
+
w
22
(
3
)
a
2
(
2
)
+
w
23
(
3
)
a
3
(
2
)
+
b
2
(
3
)
)
)
2
]
E=\frac{1}{2}\begin{bmatrix} (y_1-f(w_{11}^{(3)}a_1^{(2)}+w_{12}^{(3)}a_2^{(2)}+w_{13}^{(3)}a_3^{(2)}+b_1^{(3)}))^2+(y_2-f(w_{21}^{(3)}a_1^{(2)}+w_{22}^{(3)}a_2^{(2)}+w_{23}^{(3)}a_3^{(2)}+b_2^{(3)}))^2 \end{bmatrix}
E=21[(y1−f(w11(3)a1(2)+w12(3)a2(2)+w13(3)a3(2)+b1(3)))2+(y2−f(w21(3)a1(2)+w22(3)a2(2)+w23(3)a3(2)+b2(3)))2]
(
5
)
(5)
(5)
我们的目的时调整权重和偏执使总体误差减小,求得误差为最小(或某一可以接受的范围)时所对应的每个
w
i
j
(
l
)
w_{ij}^{(l)}
wij(l),
b
i
(
l
)
b_i^{(l)}
bi(l)。
训练过程的核心就是梯度下降,我们对每个参数
w
i
j
(
l
)
w_{ij}^{(l)}
wij(l),
b
i
(
l
)
b_i^{(l)}
bi(l)求偏导,通过下降这些梯度来减小损失函数
E
E
E的值,每次步长为
α
\alpha
α(学习率),这也就是每个权重的更新过程,以
w
11
(
3
)
w_{11}^{(3)}
w11(3)为例:
以
w
11
(
3
)
w_{11}^{(3)}
w11(3)为例,由链式求导法则,对
w
11
(
3
)
w_{11}^{(3)}
w11(3)求偏导结果为:
∂
E
∂
w
11
(
3
)
=
∂
E
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
w
11
(
3
)
=
∂
E
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
w
11
(
3
)
=
−
(
y
1
−
a
1
(
3
)
)
f
′
(
z
1
(
3
)
)
∂
z
1
(
3
)
∂
w
11
(
3
)
=
−
(
y
1
−
a
1
(
3
)
)
f
′
(
z
1
(
3
)
)
a
1
(
2
)
\frac{\partial E}{\partial w_{11}^{(3)}} = \frac{\partial E}{\partial z_{1}^{(3)}} \frac{\partial z_{1}^{(3)}}{\partial w_{11}^{(3)}} = \frac{\partial E}{\partial a_{1}^{(3)}} \frac{\partial a_{1}^{(3)}}{\partial z_{1}^{(3)}}\frac{\partial z_{1}^{(3)}}{\partial w_{11}^{(3)}} = -(y_1-a_1^{(3)})f^{'}(z_1^{(3)}) \frac{\partial z_{1}^{(3)}}{\partial w_{11}^{(3)}} = -(y_1-a_1^{(3)})f^{'}(z_1^{(3)}) a_1^{(2)}
∂w11(3)∂E=∂z1(3)∂E∂w11(3)∂z1(3)=∂a1(3)∂E∂z1(3)∂a1(3)∂w11(3)∂z1(3)=−(y1−a1(3))f′(z1(3))∂w11(3)∂z1(3)=−(y1−a1(3))f′(z1(3))a1(2)
(
6
)
(6)
(6)
其中偏导数
∂
E
∂
z
i
(
l
)
\frac{\partial E}{\partial z_{i}^{(l)}}
∂zi(l)∂E表示第
l
l
l层第
i
i
i个神经元对最终损失的影响,也反映了最终损失对第
l
l
l层神经元的敏感程度,因此一般称为第
l
l
l层神经元的误差项,用
δ
(
l
)
\delta^{(l)}
δ(l)来表示。
δ
(
l
)
≡
∂
E
∂
z
i
(
l
)
(
7
)
\delta^{(l)}≡\frac{\partial E}{\partial z_{i}^{(l)}}\\(7)
δ(l)≡∂zi(l)∂E(7)
∂
E
∂
w
11
(
3
)
=
∂
E
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
w
11
(
3
)
=
δ
1
(
3
)
a
1
(
2
)
(
8
)
\frac{\partial E}{\partial w_{11}^{(3)}} = \frac{\partial E}{\partial z_{1}^{(3)}} \frac{\partial z_{1}^{(3)}}{\partial w_{11}^{(3)}}=\delta_1^{(3)}a_1^{(2)}\\(8)
∂w11(3)∂E=∂z1(3)∂E∂w11(3)∂z1(3)=δ1(3)a1(2)(8)
其中:
δ
1
(
3
)
=
∂
E
∂
z
1
(
3
)
=
∂
E
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
=
−
(
y
1
−
a
1
(
3
)
)
f
′
(
z
1
(
3
)
)
\delta_1^{(3)}= \frac{\partial E}{\partial z_{1}^{(3)}}= \frac{\partial E}{\partial a_{1}^{(3)}} \frac{\partial a_{1}^{(3)}}{\partial z_{1}^{(3)}} =-(y_1-a_1^{(3)})f^{'}(z_1^{(3)})
δ1(3)=∂z1(3)∂E=∂a1(3)∂E∂z1(3)∂a1(3)=−(y1−a1(3))f′(z1(3))
对于误差项 δ \delta δ(增量),引入他除了可以简化计算 ∂ E ∂ w \frac{\partial E}{\partial w} ∂w∂E以外,更重要的是可以通过 δ ( l + 1 ) \delta^{(l+1)} δ(l+1)来求解 δ ( l ) \delta^{(l)} δ(l),这样可以便于理解和加快计算速度。
以下是输出层
(
L
)
(L)
(L)计算误差项和梯度的矩阵形式(⊙表示矩阵中对应位置元素相乘)
δ
(
L
)
=
−
(
y
−
a
(
L
)
)
⊙
f
′
(
z
(
L
)
)
△
w
(
L
)
=
δ
(
l
)
(
a
(
L
−
1
)
)
T
(
9
)
\delta^{(L)}=-(y-a^{(L)})⊙f^{'}(z^{(L)})\\△w^{(L)}=\delta^{(l)}(a^{(L-1)})^T\\(9)
δ(L)=−(y−a(L))⊙f′(z(L))△w(L)=δ(l)(a(L−1))T(9)
权重更新公式(
α
为
学
习
率
\alpha为学习率
α为学习率):
w
(
L
)
=
w
(
L
)
−
α
△
w
(
L
)
(
10
)
w^{(L)}=w^{(L)}-\alpha△w^{(L)}\\(10)
w(L)=w(L)−α△w(L)(10)
再以隐藏层的
w
11
(
2
)
w_{11}^{(2)}
w11(2)为例,按照链式求导规则可以展开为两项和:
∂
E
∂
w
11
(
2
)
=
∂
E
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
a
1
(
2
)
∂
a
1
(
2
)
∂
z
1
(
2
)
∂
z
1
(
2
)
∂
w
11
(
2
)
+
∂
E
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
∂
z
2
(
3
)
∂
a
1
(
2
)
∂
a
1
(
2
)
∂
z
1
(
2
)
∂
z
1
(
2
)
∂
w
11
(
2
)
=
−
(
y
−
a
1
(
3
)
)
f
′
(
z
1
(
3
)
)
w
11
(
3
)
f
′
(
z
1
(
2
)
)
x
1
−
(
y
−
a
2
(
3
)
)
f
′
(
z
2
(
3
)
)
w
21
(
3
)
f
′
(
z
1
(
2
)
)
x
1
=
[
(
y
−
a
1
(
3
)
)
f
′
(
z
1
(
3
)
)
w
11
(
3
)
−
(
y
−
a
2
(
3
)
)
f
′
(
z
2
(
3
)
)
w
21
(
3
)
]
f
′
(
z
1
(
2
)
)
x
1
=
(
δ
1
(
3
)
w
11
(
3
)
+
δ
2
(
3
)
w
21
(
3
)
)
f
′
(
z
1
(
2
)
)
x
1
\frac{\partial E}{\partial w_{11}^{(2)}} \\ = \frac{\partial E}{\partial a_{1}^{(3)}} \frac{\partial a_{1}^{(3)}}{\partial z_{1}^{(3)}} \frac{\partial z_{1}^{(3)}}{\partial a_{1}^{(2)}} \frac{\partial a_{1}^{(2)}}{\partial z_{1}^{(2)}} \frac{\partial z_{1}^{(2)}}{\partial w_{11}^{(2)}} + \frac{\partial E}{\partial a_{2}^{(3)}} \frac{\partial a_{2}^{(3)}}{\partial z_{2}^{(3)}} \frac{\partial z_{2}^{(3)}}{\partial a_{1}^{(2)}} \frac{\partial a_{1}^{(2)}}{\partial z_{1}^{(2)}} \frac{\partial z_{1}^{(2)}}{\partial w_{11}^{(2)}}\\ = -(y-a_1^{(3)})f^{'}(z_1^{(3)})w_{11}^{(3)}f^{'}(z_1^{(2)})x1 - (y-a_2^{(3)})f^{'}(z_2^{(3)})w_{21}^{(3)}f^{'}(z_1^{(2)})x1\\ =\begin{bmatrix} (y-a_1^{(3)})f^{'}(z_1^{(3)})w_{11}^{(3)} - (y-a_2^{(3)})f^{'}(z_2^{(3)})w_{21}^{(3)} \end{bmatrix} f^{'}(z_1^{(2)})x1\\ =(\delta_1^{(3)}w_{11}^{(3)}+\delta_2^{(3)}w_{21}^{(3)})f^{'}(z_1^{(2)})x1
∂w11(2)∂E=∂a1(3)∂E∂z1(3)∂a1(3)∂a1(2)∂z1(3)∂z1(2)∂a1(2)∂w11(2)∂z1(2)+∂a2(3)∂E∂z2(3)∂a2(3)∂a1(2)∂z2(3)∂z1(2)∂a1(2)∂w11(2)∂z1(2)=−(y−a1(3))f′(z1(3))w11(3)f′(z1(2))x1−(y−a2(3))f′(z2(3))w21(3)f′(z1(2))x1=[(y−a1(3))f′(z1(3))w11(3)−(y−a2(3))f′(z2(3))w21(3)]f′(z1(2))x1=(δ1(3)w11(3)+δ2(3)w21(3))f′(z1(2))x1
(
12
)
(12)
(12)
又因为:
∂
E
∂
w
11
(
2
)
=
∂
E
∂
z
1
(
2
)
∂
z
1
(
2
)
∂
w
11
(
2
)
=
δ
1
(
2
)
x
1
\frac{\partial E}{\partial w_{11}^{(2)}} = \frac{\partial E}{\partial z_{1}^{(2)}} \frac{\partial z_{1}^{(2)}}{\partial w_{11}^{(2)}} = \delta_1^{(2)}x_1
∂w11(2)∂E=∂z1(2)∂E∂w11(2)∂z1(2)=δ1(2)x1
(
13
)
(13)
(13)
由
(
12
)
(
13
)
(12)(13)
(12)(13)可得:
∂
E
∂
w
11
(
2
)
=
(
δ
1
(
3
)
w
11
(
3
)
+
δ
2
(
3
)
w
21
(
3
)
)
f
′
(
z
1
(
2
)
)
x
1
=
δ
1
(
2
)
x
1
\frac{\partial E}{\partial w_{11}^{(2)}}\\ =(\delta_1^{(3)}w_{11}^{(3)}+\delta_2^{(3)}w_{21}^{(3)})f^{'}(z_1^{(2)})x1\\ =\delta_1^{(2)}x_1
∂w11(2)∂E=(δ1(3)w11(3)+δ2(3)w21(3))f′(z1(2))x1=δ1(2)x1
从以上公式可以看出,第
l
l
l层的误差项可以通过第
l
+
1
l+1
l+1层的误差项计算得到,这就是误差的反向传播。
反向传播算法的含义是:第
l
l
l层的一个神经元的误差项是所有与该神经元相连的第
l
+
1
l+1
l+1层的神经元的误差项的权重和。然后,再乘上该神经元激活函数的梯度。
以矩阵的形式可以写为:
δ
(
l
)
=
(
(
W
(
l
+
1
)
)
T
δ
(
l
+
1
)
)
⊙
f
′
(
z
(
l
)
)
△
w
(
L
)
=
δ
(
L
)
X
T
(
14
)
\delta^{(l)}=((W^{(l+1)})^T\delta^{(l+1)})⊙f^{'}(z^{(l)})\\ △w^{(L)}=\delta^{(L)}X^T\\ (14)
δ(l)=((W(l+1))Tδ(l+1))⊙f′(z(l))△w(L)=δ(L)XT(14)
Python实现BP求解异或问题
# -*- coding: utf-8 -*-
import numpy as np
# 双曲正切函数,该函数为奇函数
def tanh(x):
return np.tanh(x)
# tanh导函数性质:f'(t) = 1 - f(x)^2
def tanh_prime(x):
return 1.0 - tanh(x) ** 2
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
"""
:参数layers: 神经网络的结构(输入层-隐含层-输出层包含的结点数列表)
:参数activation: 激活函数类型
"""
if activation == 'tanh': # 也可以用其它的激活函数
self.activation = tanh
self.activation_prime = tanh_prime
else:
pass
# 存储权值矩阵
self.weights = []
# range of weight values (-1,1)
# 初始化输入层和隐含层之间的权值
print('------------------', len(layers)) # 3
for i in range(1, len(layers) - 1):
# layer[i-1]+1 = layer[0]+1 = 2+1 = 3
# layers[i] + 1 = layer[1]+1 = 3
r = 2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1 # add 1 for bias node
self.weights.append(r)
# 初始化输出层权值
r = 2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1
self.weights.append(r)
def fit(self, X, Y, learning_rate=0.2, epochs=10000):
# 将一列一加到X
# 这是为了将偏置单元添加到输入层
# np.hstack()将两个数组按水平方向组合起来, 4*2 --> 4*3
X = np.hstack([np.ones((X.shape[0], 1)), X])
for k in range(epochs): # 训练固定次数
# if k % 1000 == 0: print('epochs:', k)
# 从区间中的离散均匀分布返回随机整数 [0, low).[0, 4)
i = np.random.randint(X.shape[0], high=None)
a = [X[i]] # 从m个输入样本中随机选一组
# len(self.weights) 2
for l in range(len(self.weights)):
# 每组输入样本(第一列未偏执值b)与权值进行矩阵相乘,a:1*3, weights:3*3 ---> 1*3
dot_value = np.dot(a[l], self.weights[l]) # 权值矩阵中每一列代表该层中的一个结点与上一层所有结点之间的权值
activation = self.activation(dot_value) # 放入激活函数
a.append(activation)
'''
反向传播算法的含义是:第l层的一个神经元的误差项delta(l)是
所有与该神经元相连的第l+1层的神经元的误差项delta(l+1)的权重
和。然后,再乘上该神经元激活函数的梯度。
'''
# 均方误差函数 E = 1/2 * (Y - a)**2
# 反向递推计算delta:从输出层开始,先算出该层的delta,再向前计算
error = Y[i] - a[-1] # 计算输出层delta
deltas = [error * self.activation_prime(a[-1])]
# 从倒数第2层开始反向计算delta
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_prime(a[l]))
# [level3(output)->level2(hidden)] => [level2(hidden)->level3(output)]
deltas.reverse() # 逆转列表中的元素
# backpropagation
# 1. 将其输出增量与输入激活相乘,得到权重的梯度。
# 2. 从权重中减去渐变的比率(百分比)。
for i in range(len(self.weights)): # 逐层调整权值
layer = np.atleast_2d(a[i]) # 将输入作为至少具有两个维度的数组查看
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * np.dot(layer.T, delta) # 每输入一次样本,就更新一次权值
def predict(self, x):
a = np.concatenate((np.ones(1), np.array(x))) # a为输入向量(行向量)
for l in range(0, len(self.weights)): # 逐层计算输出
a = self.activation(np.dot(a, self.weights[l]))
return a
if __name__ == '__main__':
nn = NeuralNetwork([2, 2, 1]) # 网络结构: 2输入1输出,1个隐含层(包含2个结点)
X = np.array([[0, 0], # 输入矩阵(每行代表一个样本,每列代表一个特征)
[0, 1],
[1, 0],
[1, 1]])
Y = np.array([0, 1, 1, 0]) # 期望输出
nn.fit(X, Y) # 训练网络
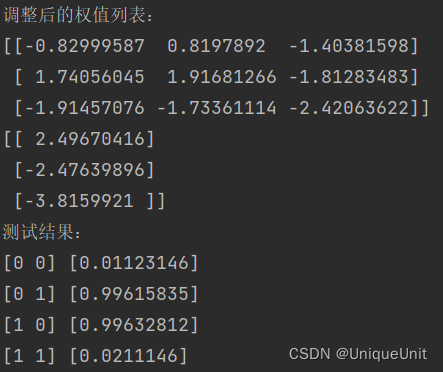
print('w:', nn.weights) # 调整后的权值列表
for s in X:
print(s, nn.predict(s)) # 测试
运行结果:




















 423
423











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








