1101: [POI2007]Zap
Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 1400 Solved: 455
[ Submit][ Status]
Description
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
Input
第一行包含一个正整数n,表示一共有n组询问。(1<=n<= 50000)接下来n行,每行表示一个询问,每行三个正整数,分别为a,b,d。(1<=d<=a,b<=50000)
Output
对于每组询问,输出到输出文件zap.out一个正整数,表示满足条件的整数对数。
Sample Input
4 5 2
6 4 3
Sample Output
2
HINT
对于第一组询问,满足条件的整数对有(2,2),(2,4),(4,2)。对于第二组询问,满足条件的整数对有(6,3),(3,3)。
莫比乌斯函数。
先把题目转化为求x<=a/d,y<=b/d且gcd(x,y)=1的(x,y)有多少对。
而莫比乌斯函数有一个性质是
这里的n=1与gcd(x,y)=1相似。
(下面引用自 iwtwiioi)
如果直接枚举d来做会TLE,但是我们发现a'/d的值在d等于好多值得时候都是相同的。
比如a'=100,那么d在[34,50]之间a'/d都是2。
那么我们可以把连续的一段d一起来算(分块):
设a'/d=x,那么最后一个a'/d=x的d=a'/x,所以这段连续的区间就是[d,a'/(a'/d)]
结合b'/d,取个min就可以了。
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#define LL long long
using namespace std;
int check[50005],mu[50005],p[50005],sum[50005];
void Getmobius()
{
memset(check,0,sizeof(check));
mu[1]=1;
int tot=0;
for (int i=2;i<=50000;i++)
{
if (!check[i])
{
p[++tot]=i;
mu[i]=-1;
}
for (int j=1;j<=tot;j++)
{
if (i*p[j]>50000) break;
check[i*p[j]]=1;
if (i%p[j]==0)
{
mu[i*p[j]]=0;
break;
}
else mu[i*p[j]]=-mu[i];
}
}
sum[0]=0;
for (int i=1;i<=50000;i++)
sum[i]=sum[i-1]+mu[i];
}
int main()
{
Getmobius();
int T;
scanf("%d",&T);
while (T--)
{
int a,b,D;
scanf("%d%d%d",&a,&b,&D);
int pos;
a/=D,b/=D;
int x=min(a,b);
LL ans=0LL;
for (int d=1;d<=x;d=pos+1)
{
pos=min(a/(a/d),b/(b/d));
ans+=(LL)(sum[pos]-sum[d-1])*(a/d)*(b/d);
}
printf("%lld\n",ans);
}
return 0;
}

感悟:
1.RE是因为数组开小。。
2.这道题的关键在于:把如果gcd(x,y)=1对答案贡献为1转化为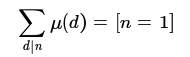
以及分块处理加速计算
3.莫比乌斯函数的求法就是线性筛,保证每个数只被算过一次,复杂度O(n)








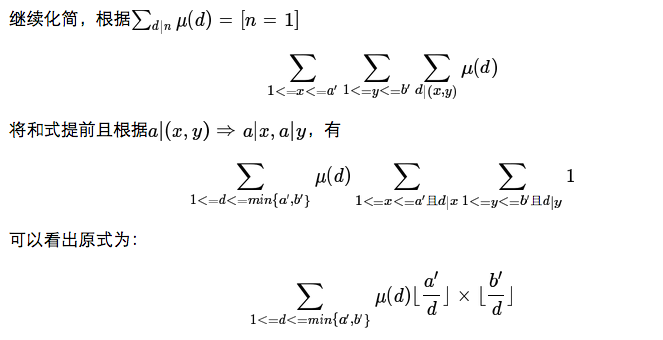














 568
568

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








