tensorflow 学习笔记12 循环神经网络RNN LSTM结构实现MNIST手写识别

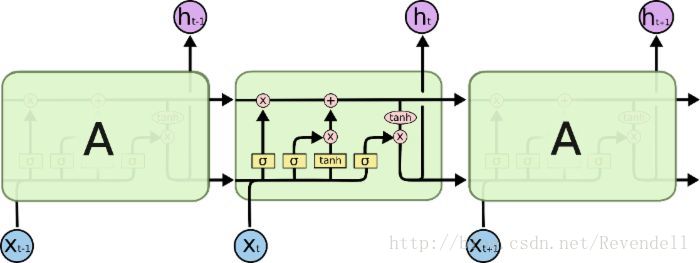
长短时记忆网络（LSTM）就是为了解决在复杂的场景中，有用信息的间隔有大有小、长短不一问题。LSTM是一种拥有三个门结构的特殊网络结构。

LSTM靠一些门的结构让信息有选择的影响循环神经网络中每个时刻的状态。所谓门的结构就是一个使用sigmoid神经网络和按位做乘法的操作，这两个操作合在一起就是一个门的结构。当门打开时（sigmoid神经网络层输出为1时），全部信息都可以通过;当门关上时（sigmoid神经网络层输出为0时），任何信息都无法通过。

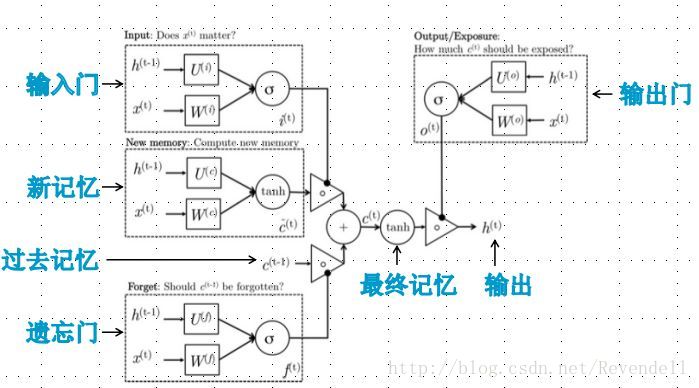
输入门（什么信息更新）：it=sigmoid(wi*[ht-1,xt]+bi)

遗忘门（丢弃什么信息）：ft=sigmoid(wf*[ht-1,xt]+bf)

输出门（确定什么信息输出）：ot=sigmoid(wo*[ht-1,xt]+bo)

信息流：ht-1 xt  ct-1

新信息：new=tanh(wc*[ht-1,xt]+bt)

历史信息累积：ct=ft*ct-1+it*new

输出信息：ht=ot*tanh(ct)

代码实现：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# configuration
#                        O * W + b -> 10 labels for each image, O[? 128], W[128 10], B[10]
#                       ^ (O: output 28 vec from 28 vec input)
#                       |
#      +-+  +-+       +--+
#      |1|->|2|-> ... |28| n_steps = 28
#      +-+  +-+       +--+
#       ^    ^    ...  ^
#       |    |         |
# img1:[28] [28]  ... [28]
# img2:[28] [28]  ... [28]
# img3:[28] [28]  ... [28]
# ...
# img128(batch_size=128)
# each input size =28

# hyperparameters
learning_rate = 0.001
training_iters = 100000
batch_size = 128

n_inputs = 28   # 输入向量的维度
n_steps = 28    # 循环层长度
n_hidden_units = 128   # neurons in hidden layer 隐含层的特征数
n_classes = 10      # MNIST classes (0-9 digits)

# X, input shape: (batch_size, n_steps, n_inputs)
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
#y, shape:(batch_size,n_classes)
y = tf.placeholder(tf.float32, [None, n_classes])

# Define weights and biases
#in:每个cell输入的全连接层参数
#out:定义用于输出的全连接层参数
weights = {
    # (28, 128)
    'in': tf.Variable(tf.random_normal([n_inputs, n_hidden_units])),
    # (128, 10)
    'out': tf.Variable(tf.random_normal([n_hidden_units, n_classes]))
}
biases = {
    # (128, )
    'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_units, ])),
    # (10, )
    'out': tf.Variable(tf.constant(0.1, shape=[n_classes, ]))
}


def RNN(X, weights, biases):
    # hidden layer for input to cell
    ########################################
    # X (128 batch,28 steps,28 inputs) ==> (128 batch * 28 steps, 28 inputs)
    X = tf.reshape(X, [-1, n_inputs])
    # into hidden
    # X_in =[128 bach*28 steps,28 inputs]*[28 inputs,128 hidden_units]=[128 batch * 28 steps, 128 hidden]
    X_in = tf.matmul(X, weights['in']) + biases['in']
    # X_in ==> (128 batch, 28 steps, 128 hidden)
    X_in = tf.reshape(X_in, [-1, n_steps, n_hidden_units])

    # cell
    #############################################
    # basic LSTM Cell.初始的bias=1,不希望遗忘任何信息
    cell = tf.contrib.rnn.BasicLSTMCell(n_hidden_units,forget_bias=1.0,state_is_tuple=True)
    # lstm cell is divided into two parts (c_state, h_state)
    init_state = cell.zero_state(batch_size, dtype=tf.float32)
    # dynamic_rnn receive Tensor (batch, steps, inputs) or (steps, batch, inputs) as X_in.
    # n_steps位于次要维度 time_major=False
    outputs, final_state = tf.nn.dynamic_rnn(cell, X_in, initial_state=init_state, time_major=False)

    # hidden layer for output as the final results
    #############################################
    # unpack to list [(batch, outputs)..] * steps
    # permute time_step_size and batch_size,[28, 128, 28]
    outputs = tf.unstack(tf.transpose(outputs, [1,0,2]))
    #选择最后一个output与输出的全连接weights相乘再加上biases
    results = tf.matmul(outputs[-1], weights['out']) + biases['out']    # shape = (128, 10)
    return results

pred = RNN(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
train_op = tf.train.AdamOptimizer(learning_rate).minimize(cost)

correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

with tf.Session() as sess:
    # 初始化
    init = tf.global_variables_initializer()
    sess.run(init)
    step = 0
    # 持续迭代
    while step * batch_size < training_iters:
        # 随机抽出这一次迭代训练时用的数据
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        # 对数据进行处理，使得其符合输入
        batch_xs = batch_xs.reshape([batch_size, n_steps, n_inputs])
        #迭代
        sess.run([train_op], feed_dict={x: batch_xs,y: batch_ys,})
        # 在特定的迭代回合进行数据的输出
        if step % 20 == 0:
            #输出准确度
            print(sess.run(accuracy, feed_dict={x: batch_xs,y: batch_ys,}))
        step += 1

结果：