科普文：算法和数据结构系列【数据库喜欢的数据结构：B-树、B+树原理、应用、以及java实现示例】

本文链接：https://blog.csdn.net/Rookie_CEO/article/details/145133448

概叙

科普文：算法和数据结构系列【非线性数据结构：树Tree和堆Heap的原理、应用、以及java实现】-CSDN博客

科普文：算法和数据结构系列【二叉树总结-上篇：满二叉树、完全二叉树、大顶堆/小顶堆、二叉搜索树、自平衡二叉树、红黑树总结】-CSDN博客

科普文：算法和数据结构系列【二叉树总结-下篇：满二叉树、完全二叉树、大顶堆/小顶堆、二叉搜索树、自平衡二叉树、红黑树总结】-CSDN博客

前面从树、二叉树、完全二叉树、搜索树、平衡树到大顶堆/小顶堆，AVL树、红黑树，我们都做了梳理：功能包括插入、删除、搜索、三种深度优先遍历（前序遍历、中序遍历、后序遍历）、一种广度优先遍历“层次遍历”、平衡操作（左旋、右旋），演示了如何构建树，如何操作树。到最后只有追求有序性和平衡性的大顶堆/小顶堆，AVL树、红黑树得到了应用。

大顶堆与小顶堆：大顶堆是一种特殊的完全二叉树，其中每个父节点的值都大于或等于其子节点的值。小顶堆则相反，每个父节点的值都小于或等于其子节点的值。

用途：大顶堆常用于实现优先队列，特别是在需要快速访问最大元素的场景中。小顶堆则适用于需要快速访问最小元素的情况。
操作效率：堆的插入和删除操作（调整为堆性质）通常具有O(log n)的时间复杂度，适合频繁的插入和删除操作，而查找最大或最小元素是O(1)。

AVL树与红黑树：AVL树和红黑树都是自平衡的二叉搜索树，用于快速查找、插入和删除数据。

平衡策略：
- AVL树：严格平衡，任何两个子树的高度差不超过1，这使得AVL树的高度较低，查找效率高，但维护平衡的代价较大，特别是在插入和删除操作时可能需要多次旋转。
- 红黑树：较弱的平衡，保证任意节点的两个子树高度差最多为2倍，这使得它在某些情况下高度略高于AVL树，但插入和删除操作的旋转次数较少，且不需要像AVL那样严格平衡，因此在实际应用中可能更高效。
操作复杂度：
- 查找：两者都是O(log n)，但由于AVL树更平衡，理论上查找路径可能更短。
- 插入与删除：AVL树在最坏情况下可能需要O(log n)次旋转来重新平衡，而红黑树保证每次插入或删除最多需要O(log n)次颜色改变和最多三次旋转，这在实践中可能更快。
空间开销：两者相似，但红黑树的实现可能稍微简单一些，因为它不需要像AVL树那样严格的平衡信息。

为啥数据库没有采用这些数据结构？

数据库没有采用大顶堆/小顶堆，AVL树、红黑树，而是选择平衡树的变种多路搜索平衡树BTree（B-Tree，B+Tree），主要原因是IO，未来当IO不再是瓶颈时，未尝不可采用这些结果来处理数据。

IO（Input/Output）操作是指从磁盘中读取或写入数据的过程。

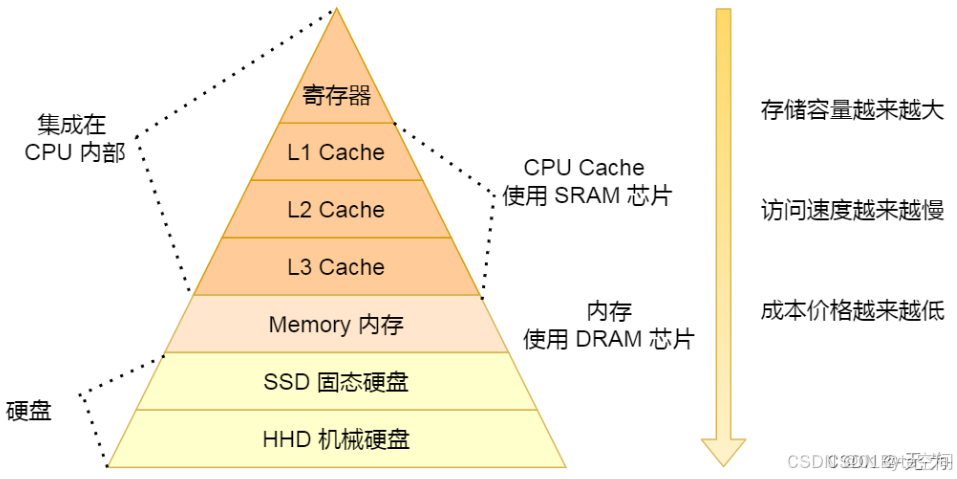
IO操作是数据库性能的瓶颈之一，因为相对于内存来说，磁盘的读写速度较慢，每次进行IO操作都需要耗费时间和资源。

因此在数据库中，只有尽量减少IO操作的次数，才能更好的提高数据库性能。为了达到这个目的通常采用分块读取、局部性原理，这两个操作的代名词就是建索引：

科普文：软件架构Linux系列之【图解存储 IO性能优化与瓶颈分析】-CSDN博客

分块读取：将磁盘上的数据划分为若干块，每次读取一块数据，减少了单次IO操作的数据量。这样做的好处是，如果我们只需要查询某个块中的数据，就不需要读取整个表或索引的数据，从而减少了IO操作次数。
局部性原理：局部性原理是指在某一次IO操作中，很有可能会连续读取到相邻的数据块。这是因为数据库索引的数据通常是按照一定的顺序存储在磁盘上的。当我们查询某个索引时，由于数据的有序性，磁盘预读机制会帮助我们预先将相邻的数据块读入内存，提高查询效率。

红黑树在数据库索引中较为常见，而AVL树由于维护成本较高，实际应用较少。大顶堆和小顶堆则在特定的排序和优先级处理中发挥作用，而不是作为主要的索引结构。

从索引存储数据量来讲：

100万条数据，主键int采用二叉树（无论是大顶堆/小顶堆、AVL树、还是红黑树），其二叉树高度是2为底100万的对数log₂(1000000) ≈ 19.93，需要20次io；

100万个int类型的数据，B+树的索引高度远低于二叉树，且查询性能更优。因此，在数据库索引等需要高效查询的场景中，B+树是更为合适的选择。具体来说：

‌二叉树索引高度‌：
- 在最坏情况下（如数据递增插入），二叉树会退化为链表，索引高度达到100万，查询性能极低。
- 即使在理想平衡状态下，二叉树的平均高度也接近log₂(1000000) ≈ 19.93，即大约20层‌。
‌B+树索引高度‌：
- B+树是多路平衡查找树，节点可以包含多个子节点，因此树的高度远低于二叉树。
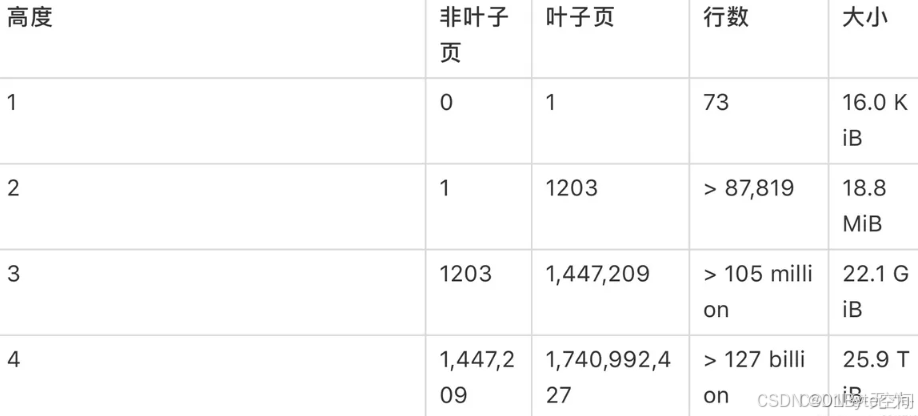
- B+树的高度取决于节点的度（即每个节点可以包含的子节点数量）和数据的总量。在实际应用中，B+树的高度通常只有1-4层不等‌。4层的B+树就能存储1447209个int。
- 由于B+树的高度较低，且其设计优化了磁盘I/O操作，因此查询性能远高于二叉树‌。

科普文：软件架构数据库系列之【详解MySQL索引：innodb索引高度和表的容量限制】-CSDN博客

‌在数据库中，常见的用到树形结构来存储数据或者索引的包括二叉树、AVL树和红黑树等，但大顶堆和小顶堆通常不是数据库索引的直接选择‌。以下是一些具体的应用实例：

‌二叉树‌：虽然二叉树在数据库索引中使用较少，因为其查询性能相对较低，但在某些特定场景下，如简单的键值对存储或内存数据库（如Redis的某些数据结构）中，可能会用到二叉树或其变种‌。
‌AVL树‌：AVL树是一种自平衡的二叉搜索树，其特点是任意节点的左子树和右子树的高度差不超过1。这种平衡性使得AVL树在插入、删除和查找操作时都能保持较高的效率。然而，在数据库索引中，AVL树并不是最常见的选择，因为对于大量数据的存储和检索，B-Tree或其变种（如B+Tree）通常更为高效‌。但在某些需要高度平衡二叉树的场景中，AVL树可能会被使用。
‌红黑树‌：红黑树也是一种自平衡的二叉搜索树，它通过一系列的规则（如节点颜色、左旋、右旋等）来保持树的平衡。红黑树在插入、删除和查找操作时也能保持较高的效率，并且其平衡性使得它在实际应用中表现良好。在某些数据库系统中，红黑树可能被用作内部数据结构或索引的一部分‌。

至于大顶堆和小顶堆，它们通常是用于实现优先队列等数据结构，而不是直接用于数据库索引。数据库索引的主要目的是提高数据检索的效率，而堆结构更适合于处理动态的数据集合，如任务调度、事件处理等场景。

虽然二叉树、AVL树和红黑树等树形结构在数据库中有一定的应用，但B-Tree及其变种（如B+Tree）通常是数据库索引的首选结构，因为它们能够更有效地处理大量数据的存储和检索需求‌。

数据库为啥选择B+Tree来做索引的数据结构？

B+Tree通过其结构设计和与磁盘交互的方式，有效地减少了数据库查询中的磁盘I/O操作次数，提高了数据访问的速度，这对于性能敏感的数据库应用至关重要。

以下是B+Tree优化磁盘I/O的关键点：（分块读取和局部性原理）

节点扇出（Fan-out）大：B+Tree的每个节点可以存储大量的键值对，尤其是内部节点只存储键而不存储数据，这使得每个节点能够包含更多的指针，减少树的高度。高度的减少意味着从根到叶子节点的路径更短，从而减少了磁盘I/O次数。
所有数据位于叶子节点：在B+Tree中，所有实际的数据都存储在叶子节点上，且叶子节点通过双向链表相连。这意味着进行范围查询时，只需要访问叶子节点，而不需要回溯到父节点，减少了磁盘访问。一次遍历叶子节点链表即可完成范围数据的读取，大大提升了效率。
节点大小与磁盘页对齐：为了高效利用缓存和磁盘的读写机制，B+Tree的节点大小通常设计得与操作系统管理的磁盘页大小一致（通常是4KB）。这样，读取一个节点就相当于一次磁盘I/O，且能最大限度地利用每次读写的容量，减少I/O次数。
减少分裂操作：通过精心设计节点的填充率，B+Tree力求在插入新元素时避免频繁的节点分裂。节点在达到一定阈值前会尝试合并或重新分配元素，以维持节点的半满状态，减少因节点分裂导致的额外I/O。
顺序访问优化：由于叶子节点通过链表相连，对于需要顺序访问数据的场景，B+Tree可以提供连续的磁盘块访问，这在磁盘I/O中是非常高效的，因为磁盘的顺序读取速度远高于随机读取。
索引与数据分离：内部节点仅包含索引信息，不直接存储数据，这使得索引结构更加紧凑，进一步减少I/O次数，尤其是在进行索引查找时。

B-Tree和B+Tree

B-tree和B+tree都是自平衡的多路搜索树，它们在数据结构和数据库索引中有广泛应用，但两者在节点存储数据方式、叶子节点结构、搜索效率、范围查询能力等方面存在显著差异‌。

‌节点存储数据的方式‌：
- ‌B-tree‌：在B-tree中，所有的节点（包括叶子节点和内部节点）都可以存储数据记录（关键字）。每个节点不仅存储键值，还存储对应的指向数据记录的指针，或者是数据本身‌。
- ‌B+tree‌：在B+tree中，只有叶子节点才存储数据记录，内部节点仅存储键值（用于导航）。因此，B+tree的内部节点只充当索引作用，不存储实际的数据‌。
‌叶子节点的结构‌：
- ‌B-tree‌：B-tree的叶子节点不一定是链接在一起的，每个叶子节点之间没有直接的链接‌。
- ‌B+tree‌：B+tree的叶子节点通常是链表式连接的，即每个叶子节点都指向下一个叶子节点。这使得B+tree在范围查询时非常高效，因为可以沿着叶子节点链表顺序访问数据‌。
‌搜索效率‌：
- ‌B-tree‌：由于每个节点都存储数据，并且内部节点直接与数据记录关联，因此在查找某个数据时，可能需要遍历多个节点并访问数据。相对来说，搜索过程可能稍慢一些‌。
- ‌B+tree‌：由于内部节点只存储索引值，不存储实际数据，搜索过程通常更快一些。B+tree通过将所有数据存储在叶子节点，并且叶子节点之间按顺序链接，能够在进行范围查询时更高效‌。
‌范围查询能力‌：
- ‌B-tree‌：范围查询时，需要遍历多个节点，且叶子节点之间没有链接，因此对范围查询的支持较差‌。
- ‌B+tree‌：由于叶子节点形成了一个链表，B+tree在范围查询时表现优异，可以直接按顺序遍历叶子节点，大大提高了范围查询的效率‌。
‌树的高度与磁盘I/O‌：
- ‌B-tree与B+tree‌：两者都通过每个节点存储多个数据（多个键值）来减少树的高度，从而降低磁盘I/O成本。然而，由于B+tree的所有数据存储在叶子节点，且内部节点较“瘦”，不存储数据，因此在相同数据量下，B+tree可能需要更多的节点来支持数据存储，但其高度通常仍然较低，因为内部节点只存储索引‌。
‌应用场景‌：
- ‌B-tree‌：适用于那些对范围查询要求不高，但需要高效执行单点查询和更新操作的场景‌。
- ‌B+tree‌：非常适合大规模数据存储和检索系统，特别是需要高效范围查询的场景，如数据库索引‌。

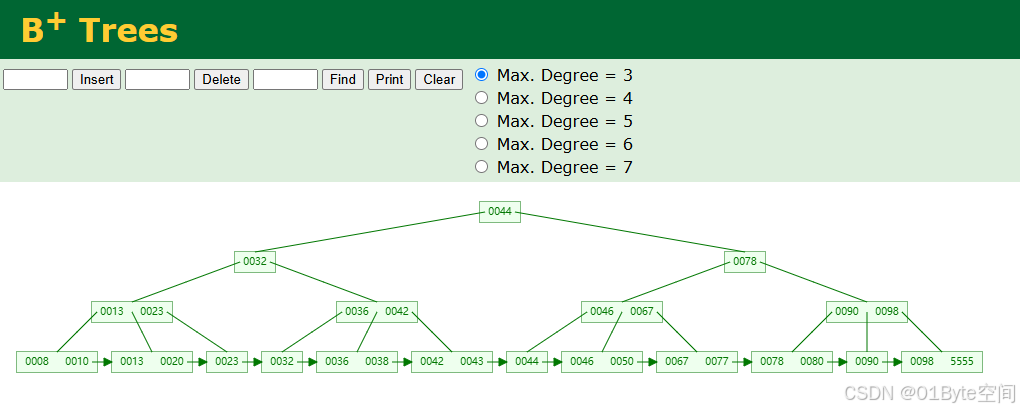
体验B+tree的结构操作，可参考网站：B+ Tree Visualization

B类型树

什么是B树/B类型树？

B树不要和B-tree搞混了。B 树又叫平衡多路查找树。

B树是一种多路搜索树，每个节点可以有多个子节点和键值。B树的关键特性包括：

‌节点中的键值按照升序排列‌，并作为子树的分隔键。
‌每个键值将节点分割成多个子树‌，每个子树由一个子节点指针指向。
‌叶子节点通常包含指向实际记录的指针‌。
‌B树的阶（或分支因子）定义了节点可以拥有的最大子节点数‌。

一棵m阶的B 树 (注：切勿简单的认为一棵m阶的B树是m叉树，虽然存在四叉树，八叉树，KD树，及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树，但与B树完全不等同)的特性如下：

①树中每个结点最多含有m个孩子（m>=2）；

②除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；

③若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；

④所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；（读者反馈@冷岳：这里有错，叶子节点只是没有孩子和指向孩子的指针，这些节点也存在，也有元素。@研究者July：其实，关键是把什么当做叶子结点，因为如红黑树中，每一个NULL指针即当做叶子结点，只是没画出来而已）。

⑤每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中： a)Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。 b)Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。 c)关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。如下图所示：

B类型树分类

‌B类型树主要包括B-tree（B-树）、B+tree（B+树）和B*tree（B*树）‌。

‌B-tree（B树）‌：

B-tree是一种自平衡的多路搜索树，其每个节点可以包含多个子节点和多个关键字。
节点内的关键字按顺序存储，且每个关键字都对应一个子节点的指针。
B-tree的高度较低，因此搜索、插入和删除操作都相对高效。
在数据库索引等需要高效存储和检索大量数据的场景中，B-tree有广泛应用‌。

一棵M阶B树(M阶数：表示此树的结点最多有多少个孩子结点(子树))是一棵平衡的m路搜索树。它或者是空树，或者是满足下列性质的树：

每个节点最多包含 m 个子节点
根结点至少有两个子节点，除根节点外，每个非叶节点至少包含 m/2 个子节点；
拥有 k 个子节点的非叶节点将包含 k - 1 条记录
每个非根节点所包含的关键字个数 j 满足：┌m/2┐ - 1 <= j <= m - 1；
除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1，故内部子树个数 k 满足：┌m/2┐ <= k <= m ；
所有的叶子结点都位于同一层。

简单理解为：平衡多叉树为B树（每一个子节点上都是有数据的），叶子节点之间无指针相邻

B树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；重复，直到所对应的儿子指针为空，或已经是叶子结点

如果B树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变B树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；但B树在经过多次插入与删除后，有可能导致不同的结构

B-树的特性：

关键字集合分布在整颗树中；
任何一个关键字出现且只出现在一个结点中；
搜索有可能在非叶子结点结束；
其搜索性能等价于在关键字全集内做一次二分查找；
自动层次控制；

由于M阶B树每个结点最少M/2个结点的限制，是为了最大限度的减少查找路径的长度，提供查找效率
B树在数据库中有一些应用，如mongodb的索引使用了B树结构。但是在很多数据库应用中，使用了是B树的变种B+树.

‌B+tree（B+树）‌：

B+tree是B-tree的一种变体，其特点是所有数据都存储在叶子节点中，内部节点只存储索引值。
叶子节点之间通过指针相连，形成一个链表，便于进行范围查询。
B+tree在范围查询和顺序访问方面表现优异，因为可以直接通过叶子节点的链表顺序访问数据‌。

B+树是B树的一种变形形式，B+树上的叶子结点存储关键字以及相应记录的地址，叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下

每个结点至多有m个子女；
除根结点外，每个结点至少有[m/2]个子女，根结点至少有两个子女；
有k个子女的结点必有k个关键字

B+树的查找与B树不同，当索引部分某个结点的关键字与所查的关键字相等时，并不停止查找，应继续沿着这个关键字左边的指针向下，一直查到该关键字所在的叶子结点为止。

B+树也是多路平衡查找树，其与B树的区别主要在于：

B树中每个节点（包括叶节点和非叶节点）都存储真实的数据，B+树中只有叶子节点存储真实的数据，非叶节点只存储键。
在MySQL中，这里所说的真实数据，可能是行的全部数据（如Innodb的聚簇索引），也可能只是行的主键（如Innodb的辅助索引），或者是行所在的地址（如MyIsam的非聚簇索引)
B树中一条记录只会出现一次，不会重复出现，而B+树的键则可能重复重现——一定会在叶节点出现，也可能在非叶节点重复出现。
B+树的叶节点之间通过双向链表链接
B树中的非叶节点，记录数比子节点个数少1；而B+树中记录数与子节点个数相同。

由此，B+树与B树相比，有以下优势：

更少的IO次数：B+树的非叶节点只包含键，而不包含真实数据，因此每个节点存储的记录个数比B树多很多（即阶m更大），因此B+树的高度更低，访问时所需要的IO次数更少。此外，由于每个节点存储的记录数更多，所以对访问局部性原理的利用更好，缓存命中率更高。
更适于范围查询：在B树中进行范围查询时，首先找到要查找的下限，然后对B树进行中序遍历，直到找到查找的上限；而B+树的范围查询，只需要对链表进行遍历即可。
更稳定的查询效率：B树的查询时间复杂度在1到树高之间(分别对应记录在根节点和叶节点)，而B+树的查询复杂度则稳定为树高，因为所有数据都在叶节点。

B+树也存在劣势：由于键会重复出现，因此会占用更多的空间。但是与带来的性能优势相比，空间劣势往往可以接受，因此B+树的在数据库中的使用比B树更加广泛。

‌**Btree（B树）**‌：

B*-tree是B+-tree的变体，在B+-tree的非根和非叶子结点再增加指向兄弟的指针；B*-tree定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。给出了一个简单实例，如下图所示：

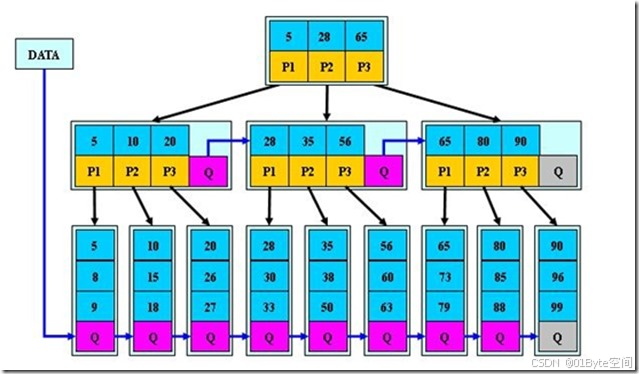
B*tree是B-tree的另一种变体，它在B-tree的基础上进行了优化，以进一步提高性能。
B*tree的特点包括非叶子节点也存储数据，且叶子节点之间通过双向链表相连。
这种结构使得B*tree在插入、删除和查找操作方面都有较好的性能表现‌。

B*树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；
B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3(代替B+树的1/2)；

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；所以，B*树分配新结点的概率比B+树要低，空间使用率更高

`B树`类型总结：

B树：有序数组+平衡多叉树
B+树：有序数组链表+平衡多叉树
B*树：一棵更丰满的，空间利用率更高的B+树

二叉搜索树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；
B树(B-树)：多路搜索树，每个结点存储M/2到M（M是指M阶B树）个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；
B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；
B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3.

B类型树优点

多路搜索：B树可以在每个节点存储更多的键值对，减少了树的高度，提高了查找效率。
磁盘友好：B树的节点大小通常与磁盘的页大小相匹配，这样可以最大化地利用磁盘的读取能力，减少I/O操作次数。
动态平衡：B树能够在插入和删除操作后自动调整结构以保持平衡状态，确保操作的时间复杂度稳定。

一些使用B-Tree、B+Tree或其变种作为索引的数据库系统包括：

‌MySQL‌：MySQL的InnoDB存储引擎使用B+Tree作为其索引结构。B+Tree在内部节点中只存储键，而在叶子节点中存储实际的数据记录或指向数据记录的指针。这种结构使得范围查询和顺序访问非常高效。
‌PostgreSQL‌：PostgreSQL也支持B-Tree索引，它同样使用B+Tree结构。用户可以通过CREATE INDEX语句为表中的一个或多个列创建B-Tree索引，以提高查询性能。
‌Oracle‌：Oracle数据库也使用B-Tree或其变种作为索引结构。Oracle的索引机制相当复杂，包括多种类型的索引，但B-Tree索引是其中一种常用的索引类型。
‌SQLite‌：SQLite是一个轻量级的嵌入式数据库，它也使用B-Tree（实际上是B+Tree）作为索引和表数据的存储结构。
MongoDB：在采用WiredTiger存储引擎之前（MongoDB 3.2 默认使用 WiredTiger 存储引擎），其基于文件的存储方式（如MMap）虽然不是直接使用标准的B-Tree，但索引结构在概念上接近于B-Tree家族，而WiredTiger内部虽然优化了存储方式，其索引机制也借鉴了B+Tree的高效性。

科普文：深入了解MongoDB_mongodb深入了解-CSDN博客

B类型树对比

‌B树（B-tree）是一种自平衡的树结构，能够保持数据有序。

‌B树的具体类型包括B-tree、B+树和B*树，它们都是B树的变体，适用于不同的场景和需求。

B-tree：B-tree是最基本的B树类型，它是一种平衡的多路查找树。B-tree的特点包括：

‌节点结构‌：每个节点可以有多个子节点，通常节点包含多个关键字，这些关键字将节点内的数据分成多个区间。
‌平衡性‌：B-tree通过一系列操作保持平衡，确保树的高度较低，从而减少磁盘I/O操作。
‌应用场景‌：广泛应用于数据库和文件系统中，特别是在处理大量数据时表现出色‌。

B+树：B+树是B-tree的变体，常用于数据库索引。B+树的特点包括：

‌节点结构‌：所有值都存储在叶子节点且叶子节点间有双向指针，非叶子节点仅存储关键字和指向子节点的指针。
‌平衡性‌：通过分裂和合并操作保持平衡。
‌应用场景‌：特别适合读操作密集的应用，因为所有数据都存储在叶子节点，读取效率高‌。

B*树：B*树是B-tree的另一个变体，它在B-tree的基础上进行了一些优化，特点包括：

‌节点结构‌：与B-tree类似，但B*树的分裂操作更复杂，确保树的平衡性更好。
‌平衡性‌：通过更复杂的分裂和合并规则来维持树的平衡。
‌应用场景‌：适用于需要极高数据完整性和一致性的场景‌。

B+Tree

三种B类型树，我们在这里主要是讲B+Tree，和B-Tree对比，B+Tree在B-Tree的基础上多了三个主要改动“所有值都存储在叶子节点且叶子节点间有双向指针，非叶子节点仅存储关键字和指向子节点的指针。”

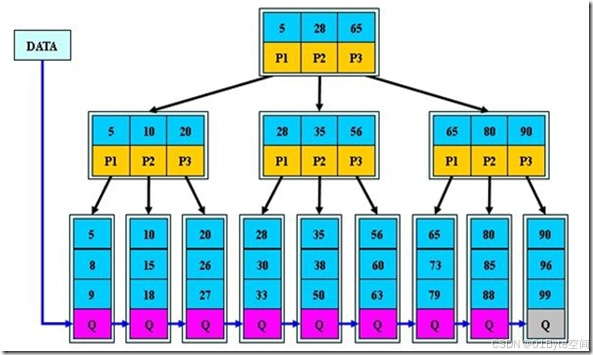
B+树是B树的一种变形形式，B+树上的叶子结点存储关键字以及相应记录的地址，叶子结点以上各层作为索引使用。

一棵m阶的B+树定义如下

每个结点至多有m个子女；
除根结点外，每个结点至少有[m/2]个子女，根结点至少有两个子女；
有k课子树的分支结点则存在k-1个关键字，关键字按照递增顺序进行排序。关键字数量满足ceil(M/2)-1 <= n <= M-1。
所有的叶结点都在同一层上；

精简描述一下：

树开叉的数量上限是M颗，也就是定义了范围。
形容M颗子树与Key值的关系。
所有的叶子节点在同一层。
除了根节点以外，每个节点最少有M÷2颗子树。

B 树中一个节点的子节点数目的最大值，用 m 表示，假如最大值为 10，则为 10 阶，如图

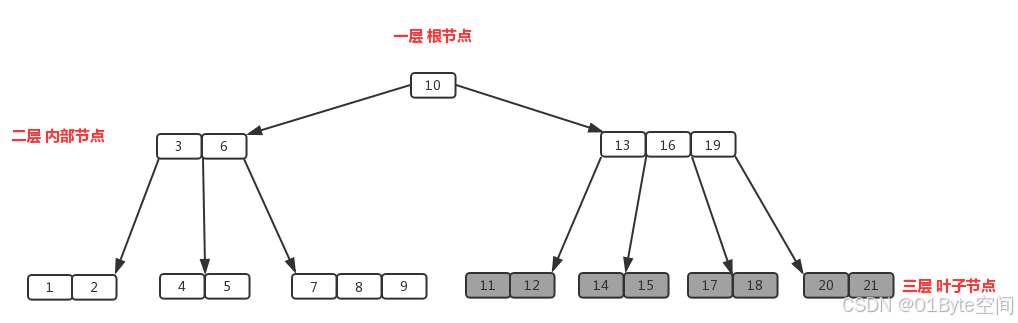
所有节点中，节点【13,16,19】拥有的子节点数目最多，四个子节点（灰色节点），所以可以定义上面的图片为 4 阶 B 树。

根节点：节点【10】即为根节点，特征：根节点拥有的子节点数量的上限和内部节点相同，如果根节点不是树中唯一节点的话，至少有俩个子节点（不然就变成单支了）。在 m 阶 B 树中（根节点非树中唯一节点），那么有关系式 2<= M <=m，M 为子节点数量；包含的元素数量 1<= K <=m-1,K 为元素数量

叶子结点：节点【1,2】、节点【11,12】等最后一层都为叶子节点，叶子节点对元素的数量有相同的限制，但是没有子节点，也没有指向子节点的指针。

特征：在 m 阶 B 树中叶子节点的元素符合（m/2）-1<= K <=m-1

B+tree主要操作

B+tree的主要操作包括搜索操作、插入操作、删除操作和修改操作‌。以下是这些操作的简要说明：

‌搜索操作‌：
- 在B+tree中，搜索操作从根节点开始，根据查询键值沿着路径向下查找。
- 非叶子节点仅存储键值和指向子节点的指针，不保存数据本身，因此搜索过程中会不断比较键值并沿着相应的指针向下移动。
- 当到达叶子节点时，搜索结束，此时能在叶子节点上定位到目标数据或者确定不存在‌。
‌插入操作‌：
- 插入操作时，首先根据键值大小找到对应位置。
- 若节点未满，则直接将键值插入到相应位置。
- 若节点已满，则进行分裂操作，将节点分裂为两个，并调整父节点的指针，以保持树的平衡‌。
‌删除操作‌：
- 删除数据时，首先找到包含要删除键值的叶子节点。
- 从叶子节点中删除键值，并调整节点的指针。
- 如果删除操作导致节点元素数量低于阈值，则可能需要合并相邻节点或重构树来保持稳定性‌。
‌修改操作‌：
- 修改操作通常涉及先执行删除操作，再执行插入操作。
- 即先删除旧的键值，然后插入新的键值到相应位置。
- 需要注意的是，修改操作也需要保持树的平衡性‌。
平衡操作：分裂和合并（插入、删除、修改都可能会导致分裂或者合并）
- ‌B+tree的主要操作中的分裂和合并是维持树平衡和高效性能的关键‌。
- 分裂操作‌：
  - ‌发生时机‌：分裂操作通常在插入新键值对时发生，特别是当叶子节点或内部节点达到其容量上限时‌。
  - ‌操作过程‌：
    - 在叶子节点中，如果节点已满，则找到节点的中点键值，将该键值提升到父节点，并将原节点分裂为两个新的叶子节点‌。
    - 在内部节点中，分裂操作类似，但提升的是中间键值对应的子节点指针，同时调整父节点的指针以保持树的连接性‌。
  - ‌结果‌：分裂操作导致树的高度可能增加，但保持了树的平衡性，使得后续的搜索、插入和删除操作仍然高效‌。
- ‌合并操作‌：
  - ‌发生时机‌：合并操作通常在删除键值对时发生，特别是当叶子节点或内部节点的键值对数量低于其容量下限时‌。
  - ‌操作过程‌：
    - 在叶子节点中，如果相邻的两个叶子节点中的键值对数量都较少（通常少于规定的最小值），则可能将它们合并为一个节点，并调整父节点的指针‌。
    - 在内部节点中，合并操作可能涉及将相邻节点的子节点指针合并到同一个节点中，同时调整父节点的键值对和指针以保持树的平衡性‌。
  - 结果‌：合并操作导致树的高度可能降低，但同样保持了树的平衡性，确保了高效的性能‌。

java模拟B+Tree

/**
 * 1. BPlusTreeNode类：表示B+树的节点，包含关键字列表、子节点列表和一个用于叶子节点链表的指针。
 * 2. BPlusTree类：表示B+树，包含插入、删除、搜索等操作。
 * 3. 插入操作：与B树类似，但在叶子节点处维护一个链表指针。
 * 4. 删除操作：此处省略了完整的删除逻辑，实际应用中需要实现。
 *
 * 注意事项：
 * 1. 删除操作：B+树的删除操作相对复杂，需要处理节点合并、关键字重新分配等情况。
 * 2. 范围查询：B+树适合范围查询，可以利用叶子节点的链表指针高效地进行范围遍历。
 *
 * @author zhouxx
 * @create 2025-01-14 0:08
 */

节点定义‘

class BPlusTreeNode {
    boolean isLeaf;
    List<Integer> keys;
    List<BPlusTreeNode> children;
    BPlusTreeNode next; // 叶子节点链表指针

    public BPlusTreeNode() {
        this.isLeaf = true;
        keys = new ArrayList<>();
        children = new ArrayList<>();
    }

    public BPlusTreeNode(boolean isLeaf) {
        this.isLeaf = isLeaf;
        keys = new ArrayList<>();
        children = new ArrayList<>();
    }
    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder("{");
        stringBuilder.append("isLeaf=").append(isLeaf).append(",");
        stringBuilder.append("children=").append(children == null ? "" : children).append(",");
        stringBuilder.append("keys=").append(keys == null ? "" : keys).append(",");
        stringBuilder.append("next=").append(next == null ? "" : next).append(",");
        stringBuilder.append("}");
        return stringBuilder.toString();
        //return value.toString();
    }
}

主类

package com.zxx.study.algorithm.datastruct.DataStructures.mtree.tree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

/**
 * 1. BPlusTreeNode类：表示B+树的节点，包含关键字列表、子节点列表和一个用于叶子节点链表的指针。
 * 2. BPlusTree类：表示B+树，包含插入、删除、搜索等操作。
 * 3. 插入操作：与B树类似，但在叶子节点处维护一个链表指针。
 * 4. 删除操作：此处省略了完整的删除逻辑，实际应用中需要实现。
 *
 * 注意事项：
 * 1. 删除操作：B+树的删除操作相对复杂，需要处理节点合并、关键字重新分配等情况。
 * 2. 范围查询：B+树适合范围查询，可以利用叶子节点的链表指针高效地进行范围遍历。
 *
 * @author zhouxx
 * @create 2025-01-14 0:08
 */
public class BPlusTree {
    private BPlusTreeNode root;
    private int t; // 最小度数

    public BPlusTree(int t) {
        this.t = t;
        root = new BPlusTreeNode(true);
    }

    // 搜索关键字
    public BPlusTreeNode search(int k) {
        return search(root, k);
    }

    private BPlusTreeNode search(BPlusTreeNode node, int k) {
        int i = 0;
        while (i < node.keys.size() && k > node.keys.get(i)) {
            i++;
        }
        if (i < node.keys.size() && k == node.keys.get(i)) {
            return node;
        }
        if (node.isLeaf) {
            return null;
        }
        return search(node.children.get(i), k);
    }

    // 插入关键字
    public void insert(int k) {
        BPlusTreeNode r = root;
        if (r.keys.size() == 2 * t - 1) {
            BPlusTreeNode s = new BPlusTreeNode(false);
            s.children.add(r);
            splitChild(s, 0, r);
            int i = 0;
            if (s.keys.get(0) < k) {
                i++;
            }
            insertNonFull(s.children.get(i), k);
            root = s;
        } else {
            insertNonFull(r, k);
        }
    }

    private void insertNonFull(BPlusTreeNode x, int k) {
        int i = x.keys.size() - 1;
        if (x.isLeaf) {
            x.keys.add(k);
            while (i >= 0 && k < x.keys.get(i)) {
                x.keys.set(i + 1, x.keys.get(i));
                i--;
            }
            x.keys.set(i + 1, k);
        } else {
            while (i >= 0 && k < x.keys.get(i)) {
                i--;
            }
            i++;
            if (x.children.get(i).keys.size() == 2 * t - 1) {
                splitChild(x, i, x.children.get(i));
                if (k > x.keys.get(i)) {
                    i++;
                }
            }
            insertNonFull(x.children.get(i), k);
        }
    }

    private void splitChild(BPlusTreeNode x, int i, BPlusTreeNode y) {
        BPlusTreeNode z = new BPlusTreeNode(y.isLeaf);
        for (int j = 0; j < t - 1; j++) {
            z.keys.add(y.keys.remove(t));
        }
        if (!y.isLeaf) {
            for (int j = 0; j < t; j++) {
                z.children.add(y.children.remove(t));
            }
        }
        x.children.add(i + 1, z);
        x.keys.add(i, y.keys.remove(t - 1));
        if (y.isLeaf) {
            z.next = y.next;
            y.next = z;
        }
    }

    // 删除关键字
    public void delete(int k) {
        delete(root, k);
        if (root.keys.isEmpty() && !root.isLeaf) {
            root = root.children.get(0);
        }
    }

    private void delete(BPlusTreeNode x, int k) {
        int idx = findKey(x, k);

        if (idx != -1) {
            if (x.isLeaf) {
                x.keys.remove(idx);
            } else {
                BPlusTreeNode predecessor = getPredecessor(x.children.get(idx));
                x.keys.set(idx, predecessor.keys.get(predecessor.keys.size() - 1));
                delete(x.children.get(idx), predecessor.keys.get(predecessor.keys.size() - 1));
            }
        } else {
            if (x.isLeaf) {
                return;
            }
            int childIdx = findChild(x, k);
            BPlusTreeNode child = x.children.get(childIdx);
            if (child.keys.size() < t) {
                fill(x, childIdx);
            }
            delete(x.children.get(childIdx), k);
        }
    }

    private int findKey(BPlusTreeNode x, int k) {
        int idx = 0;
        while (idx < x.keys.size() && x.keys.get(idx) < k) {
            idx++;
        }
        return idx < x.keys.size() && x.keys.get(idx) == k ? idx : -1;
    }

    private int findChild(BPlusTreeNode x, int k) {
        int idx = 0;
        while (idx < x.keys.size() && k > x.keys.get(idx)) {
            idx++;
        }
        return idx;
    }

    private BPlusTreeNode getPredecessor(BPlusTreeNode x) {
        while (!x.isLeaf) {
            x = x.children.get(x.children.size() - 1);
        }
        return x;
    }

    private void fill(BPlusTreeNode x, int idx) {
        if (idx != 0 && x.children.get(idx - 1).keys.size() >= t) {
            borrowFromPrev(x, idx);
        } else if (idx != x.keys.size() && x.children.get(idx + 1).keys.size() >= t) {
            borrowFromNext(x, idx);
        } else {
            if (idx != x.keys.size()) {
                merge(x, idx);
            } else {
                merge(x, idx - 1);
            }
        }
    }

    private void borrowFromPrev(BPlusTreeNode x, int idx) {
        BPlusTreeNode child = x.children.get(idx);
        BPlusTreeNode sibling = x.children.get(idx - 1);
        child.keys.add(0, x.keys.get(idx - 1));
        x.keys.set(idx - 1, sibling.keys.remove(sibling.keys.size() - 1));
        if (!child.isLeaf) {
            child.children.add(0, sibling.children.remove(sibling.children.size() - 1));
        }
    }

    private void borrowFromNext(BPlusTreeNode x, int idx) {
        BPlusTreeNode child = x.children.get(idx);
        BPlusTreeNode sibling = x.children.get(idx + 1);
        child.keys.add(x.keys.get(idx));
        x.keys.set(idx, sibling.keys.remove(0));
        if (!child.isLeaf) {
            child.children.add(sibling.children.remove(0));
        }
    }

    private void merge(BPlusTreeNode x, int idx) {
        BPlusTreeNode child = x.children.get(idx);
        BPlusTreeNode sibling = x.children.get(idx + 1);
        child.keys.add(x.keys.remove(idx));
        child.keys.addAll(sibling.keys);
        if (!child.isLeaf) {
            child.children.addAll(sibling.children);
        }
        x.children.remove(idx + 1);
    }
    // 范围查询方法：首先通过 findLeaf 方法找到包含起始关键字的叶子节点，然后沿着叶子节点的 next 指针遍历，将处于指定范围内的关键字添加到结果列表中。
    public List<Integer> rangeQuery(int start, int end) {
        List<Integer> result = new ArrayList<>();
        BPlusTreeNode leaf = findLeaf(root, start);
        while (leaf!= null) {
            for (int key : leaf.keys) {
                if (key >= start && key <= end) {
                    result.add(key);
                }
                if (key > end) {
                    return result;
                }
            }
            leaf = leaf.next;
        }
        return result;
    }
    //用于找到包含指定关键字的叶子节点
    private BPlusTreeNode findLeaf(BPlusTreeNode node, int key) {
        while (!node.isLeaf) {
            int i = 0;
            while (i < node.keys.size() && key >= node.keys.get(i)) {
                i++;
            }
            node = node.children.get(i);
        }
        return node;
    }
    //‌层次遍历（Level-order Traversal）‌：
    public void levelOrderTraversal() {
        levelOrderTraversal(root);
    }
    public void levelOrderTraversal(BPlusTreeNode root) {
        if (root == null) {
            return;
        }

        Queue<BPlusTreeNode> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            BPlusTreeNode node = queue.poll();

            System.out.println(node.toString());

            for (BPlusTreeNode child : node.children) {
                if (child != null) {
                    queue.add(child);
                }
            }
        }
    }

    // 测试用例方法
    /**
     * 1. 插入测试：插入一系列关键字，验证B+树的结构和关键字顺序是否正确。
     * 2. 搜索测试：搜索存在和不存在的关键字，验证搜索功能是否正确。
     * 3. 删除测试：删除一些关键字，验证删除功能是否正确。
     * 4. 节点分裂和合并测试：插入足够多的关键字使得节点需要分裂，删除足够多的关键字使得节点需要合并，验证节点分裂和合并功能是否正确。
     *
     * */
    public static void main(String[] args) {
        BPlusTree bplusTree = new BPlusTree(3); // 最小度数为3

        // 插入测试
        int[] insertKeys = {10, 20, 5, 6, 12, 30, 7, 17};
        for (int key : insertKeys) {
            bplusTree.insert(key);
            bplusTree.levelOrderTraversal();
            System.out.println("=================" );
        }
        System.out.println("\n=================\n" );

        // 搜索测试
        System.out.println("搜索 6: " + (bplusTree.search(6) != null)); // 应该存在
        System.out.println("搜索 15: " + (bplusTree.search(15) != null)); // 应该不存在

        // 删除测试
        int[] deleteKeys = {6, 15, 30};
        for (int key : deleteKeys) {
            bplusTree.delete(key);
        }

        // 再次搜索测试
        System.out.println("搜索 6: " + (bplusTree.search(6) != null)); // 应该不存在
        System.out.println("搜索 30: " + (bplusTree.search(30) != null)); // 应该不存在

        // 节点分裂和合并测试
        for (int i = 1; i <= 20; i++) {
            bplusTree.insert(i);
            bplusTree.levelOrderTraversal();
            System.out.println("=======分裂==========" );
        }
        System.out.println("\n=================\n" );
        for (int i = 1; i <= 10; i++) {
            bplusTree.delete(i);
            bplusTree.levelOrderTraversal();
            System.out.println("======合并===========" );
        }

        // 范围查询测试
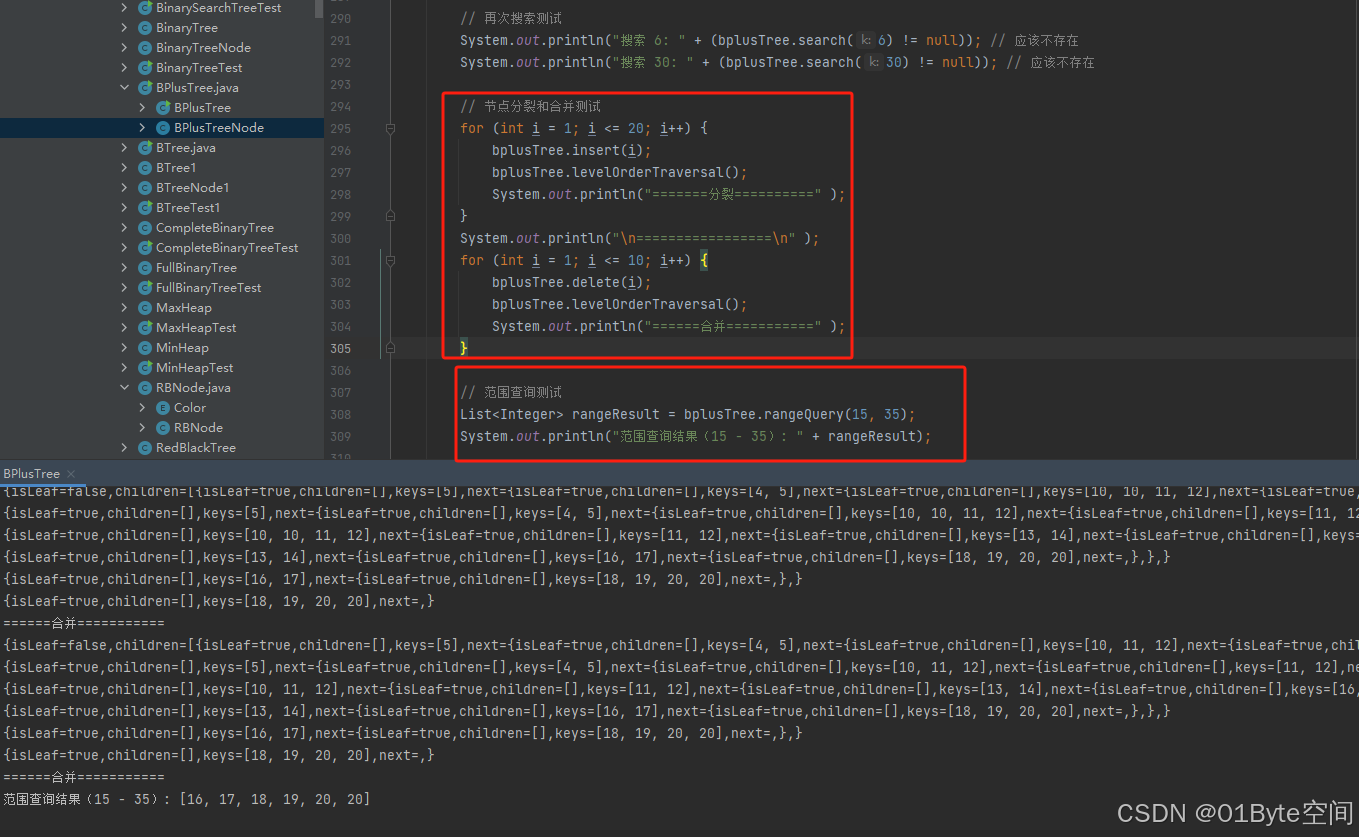
        List<Integer> rangeResult = bplusTree.rangeQuery(15, 35);
        System.out.println("范围查询结果（15 - 35）: " + rangeResult);

    }
}

// 测试用例方法
/**
* 1. 插入测试：插入一系列关键字，验证B+树的结构和关键字顺序是否正确。
* 2. 搜索测试：搜索存在和不存在的关键字，验证搜索功能是否正确。
* 3. 删除测试：删除一些关键字，验证删除功能是否正确。
* 4. 节点分裂和合并测试：插入足够多的关键字使得节点需要分裂，删除足够多的关键字使得节点需要合并，验证节点分裂和合并功能是否正确。
*
* */

重点关注：范围查询和分裂合并

java模拟B-Tree

* 1. BTreeNode类：表示B树的节点，包含关键字列表和子节点列表。
* 2. BTree类：表示B树，包含插入、删除、搜索等操作。
* 3. 插入操作：包括插入关键字和分裂节点。
* 4. 删除操作：包括删除关键字、借用关键字和合并节点。
* 5. 搜索操作：在B树中搜索关键字。
* 这个实现是一个基本的B树实现，可以根据具体需求进行优化和扩展。

b-tree的树节点定义

class BTreeNode {
    boolean isLeaf;
    List<Integer> keys;
    List<BTreeNode> children;

    public BTreeNode() {
        this.isLeaf = true;
        keys = new ArrayList<>();
        children = new ArrayList<>();
    }

    public BTreeNode(boolean isLeaf) {
        this.isLeaf = isLeaf;
        keys = new ArrayList<>();
        children = new ArrayList<>();
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder("{");
        stringBuilder.append("isLeaf=").append(isLeaf).append(",");
        stringBuilder.append("children=").append(children == null ? "" : children).append(",");
        stringBuilder.append("keys=").append(keys == null ? "" : keys).append(",");
        stringBuilder.append("}");
        return stringBuilder.toString();
        //return value.toString();
    }
}

b-tree主类操作

package com.zxx.study.algorithm.datastruct.DataStructures.mtree.tree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

/**
 * 1. BTreeNode类：表示B树的节点，包含关键字列表和子节点列表。
 * 2. BTree类：表示B树，包含插入、删除、搜索等操作。
 * 3. 插入操作：包括插入关键字和分裂节点。
 * 4. 删除操作：包括删除关键字、借用关键字和合并节点。
 * 5. 搜索操作：在B树中搜索关键字。
 * 这个实现是一个基本的B树实现，可以根据具体需求进行优化和扩展。
 * @author zhouxx
 * @create 2025-01-13 23:32
 */
public class BTree {
    private BTreeNode root;
    private int t; // 最小度数

    public BTree(int t) {
        this.t = t;
        root = new BTreeNode(true);
    }

    // 搜索关键字
    public BTreeNode search(int k) {
        return search(root, k);
    }

    private BTreeNode search(BTreeNode node, int k) {
        int i = 0;
        while (i < node.keys.size() && k > node.keys.get(i)) {
            i++;
        }
        if (i < node.keys.size() && k == node.keys.get(i)) {
            return node;
        }
        if (node.isLeaf) {
            return null;
        }
        return search(node.children.get(i), k);
    }

    // 插入关键字
    public void insert(int k) {
        BTreeNode r = root;
        if (r.keys.size() == 2 * t - 1) {
            BTreeNode s = new BTreeNode(false);
            s.children.add(r);
            splitChild(s, 0, r);
            int i = 0;
            if (s.keys.get(0) < k) {
                i++;
            }
            insertNonFull(s.children.get(i), k);
            root = s;
        } else {
            insertNonFull(r, k);
        }
    }

    private void insertNonFull(BTreeNode x, int k) {
        int i = x.keys.size() - 1;
        if (x.isLeaf) {
            x.keys.add(k);
            while (i >= 0 && k < x.keys.get(i)) {
                x.keys.set(i + 1, x.keys.get(i));
                i--;
            }
            x.keys.set(i + 1, k);
        } else {
            while (i >= 0 && k < x.keys.get(i)) {
                i--;
            }
            i++;
            if (x.children.get(i).keys.size() == 2 * t - 1) {
                splitChild(x, i, x.children.get(i));
                if (k > x.keys.get(i)) {
                    i++;
                }
            }
            insertNonFull(x.children.get(i), k);
        }
    }

    private void splitChild(BTreeNode x, int i, BTreeNode y) {
        BTreeNode z = new BTreeNode(y.isLeaf);
        for (int j = 0; j < t - 1; j++) {
            z.keys.add(y.keys.remove(t));
        }
        if (!y.isLeaf) {
            for (int j = 0; j < t; j++) {
                z.children.add(y.children.remove(t));
            }
        }
        x.children.add(i + 1, z);
        x.keys.add(i, y.keys.remove(t - 1));
    }

    // 删除关键字
    public void delete(int k) {
        delete(root, k);
        if (root.keys.isEmpty() && !root.isLeaf) {
            root = root.children.get(0);
        }
    }

    private void delete(BTreeNode x, int k) {
        int idx = findKey(x, k);

        if (idx != -1) {
            if (x.isLeaf) {
                x.keys.remove(idx);
            } else {
                BTreeNode predecessor = getPredecessor(x.children.get(idx));
                x.keys.set(idx, predecessor.keys.get(predecessor.keys.size() - 1));
                delete(x.children.get(idx), predecessor.keys.get(predecessor.keys.size() - 1));
            }
        } else {
            if (x.isLeaf) {
                return;
            }
            int childIdx = findChild(x, k);
            BTreeNode child = x.children.get(childIdx);
            if (child.keys.size() < t) {
                fill(x, childIdx);
            }
            delete(x.children.get(childIdx), k);
        }
    }

    private int findKey(BTreeNode x, int k) {
        int idx = 0;
        while (idx < x.keys.size() && x.keys.get(idx) < k) {
            idx++;
        }
        return idx < x.keys.size() && x.keys.get(idx) == k ? idx : -1;
    }

    private int findChild(BTreeNode x, int k) {
        int idx = 0;
        while (idx < x.keys.size() && k > x.keys.get(idx)) {
            idx++;
        }
        return idx;
    }

    private BTreeNode getPredecessor(BTreeNode x) {
        while (!x.isLeaf) {
            x = x.children.get(x.children.size() - 1);
        }
        return x;
    }

    private void fill(BTreeNode x, int idx) {
        if (idx != 0 && x.children.get(idx - 1).keys.size() >= t) {
            borrowFromPrev(x, idx);
        } else if (idx != x.keys.size() && x.children.get(idx + 1).keys.size() >= t) {
            borrowFromNext(x, idx);
        } else {
            if (idx != x.keys.size()) {
                merge(x, idx);
            } else {
                merge(x, idx - 1);
            }
        }
    }

    private void borrowFromPrev(BTreeNode x, int idx) {
        BTreeNode child = x.children.get(idx);
        BTreeNode sibling = x.children.get(idx - 1);
        child.keys.add(0, x.keys.get(idx - 1));
        x.keys.set(idx - 1, sibling.keys.remove(sibling.keys.size() - 1));
        if (!child.isLeaf) {
            child.children.add(0, sibling.children.remove(sibling.children.size() - 1));
        }
    }

    private void borrowFromNext(BTreeNode x, int idx) {
        BTreeNode child = x.children.get(idx);
        BTreeNode sibling = x.children.get(idx + 1);
        child.keys.add(x.keys.get(idx));
        x.keys.set(idx, sibling.keys.remove(0));
        if (!child.isLeaf) {
            child.children.add(sibling.children.remove(0));
        }
    }

    private void merge(BTreeNode x, int idx) {
        BTreeNode child = x.children.get(idx);
        BTreeNode sibling = x.children.get(idx + 1);
        child.keys.add(x.keys.remove(idx));
        child.keys.addAll(sibling.keys);
        if (!child.isLeaf) {
            child.children.addAll(sibling.children);
        }
        x.children.remove(idx + 1);
    }
    //todo 在B树（B-Tree）中，由于其特殊的结构和性质，通常不直接应用传统二叉树的遍历方法（如前序、中序、后序和层次遍历）。
    //先序遍历（Pre-order Traversal）‌：
    public void preOrderTraversal() {
        preOrderTraversal(root);
    }
    public void preOrderTraversal(BTreeNode node) {
        if (node != null) {
//            for (T key : node.keys) {
//                System.out.print(key + " ");
//            }
            System.out.println(node.toString());
            for (BTreeNode child : node.children) {
                preOrderTraversal(child);
            }
        }
    }
    //中序遍历（In-order Traversal）‌： 调用时从根节点和索引0开始
    public void inOrderTraversal() {
        inOrderTraversal(root, 0);
    }
    public void inOrderTraversal(BTreeNode node, int index) {
        if (node != null && node.children!=null && !node.children.isEmpty()) {
            inOrderTraversal(node.children.get(index), 0);
            System.out.println(node.toString());
            if (index < node.keys.size() - 1) {
                inOrderTraversal(node.children.get(index + 1), 0);
            }
            index++;
            if (index < node.children.size()) {
                inOrderTraversal(node, index);
            }
        }
    }
    //‌后序遍历（Post-order Traversal）‌：
    public void postOrderTraversal() {
        postOrderTraversal(root);
    }
    public void postOrderTraversal(BTreeNode node) {
        if (node != null) {
            for (BTreeNode child : node.children) {
                postOrderTraversal(child);
            }
            System.out.println(node.toString());
        }
    }
    //‌层次遍历（Level-order Traversal）‌：
    public void levelOrderTraversal() {
        levelOrderTraversal(root);
    }
    public void levelOrderTraversal(BTreeNode root) {
        if (root == null) {
            return;
        }

        Queue<BTreeNode> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            BTreeNode node = queue.poll();

            System.out.println(node.toString());

            for (BTreeNode child : node.children) {
                if (child != null) {
                    queue.add(child);
                }
            }
        }
    }
    /**
     * 经过检查，上述Java代码实现的B树基本功能（插入、删除、搜索、节点分裂和合并）在逻辑上是正确的，但有一些细节需要注意和改进：
     *
     * 注意事项：
     * 1. 边界条件处理：在删除操作中，处理边界条件时需要特别小心，确保不会出现数组越界等问题。
     * 2. 代码优化：可以进一步优化代码结构和性能，例如在插入和删除操作中减少不必要的列表复制和查找。
     *
     * 测试用例：为了验证B树的正确性，可以设计以下测试用例：
     *
     * 测试用例1：插入操作
     * 1. 插入关键字序列：10, 20, 5, 6, 12, 30, 7, 17
     * 2. 验证B树的结构和关键字顺序是否正确。
     *
     * 测试用例2：搜索操作
     * 1. 在上述插入操作后的B树中，搜索关键字：6, 15, 30
     * 2. 验证搜索结果是否正确（6 和 30 应该存在，15 应该不存在）。
     *
     * 测试用例3：删除操作
     * 1. 在上述插入操作后的B树中，删除关键字序列：6, 15, 30
     * 2. 验证B树的结构和关键字顺序是否正确。
     *
     * 测试用例4：节点分裂和合并
     * 1. 插入足够多的关键字，使得B树的根节点需要分裂。
     * 2. 删除足够多的关键字，使得B树的某个节点需要合并。
     * 3. 验证B树的结构和关键字顺序是否正确。
     *
     * 测试用例5：边界条件
     * 1. 插入和删除最小和最大关键字。
     * 2. 插入和删除重复关键字（B树通常不允许重复关键字，需要根据具体实现验证）。
     * */
    public static void main(String[] args) {
        BTree btree = new BTree(3); // 最小度数为3；keys最多存2 * t - 1=5个
        // 测试插入操作
        int[] insertKeys = {10, 20, 5, 6, 12, 30, 7, 17,11,90,115,50,10,20};// 有重复key，并且明显超过keys长度
        for (int key : insertKeys) {
            btree.insert(key);
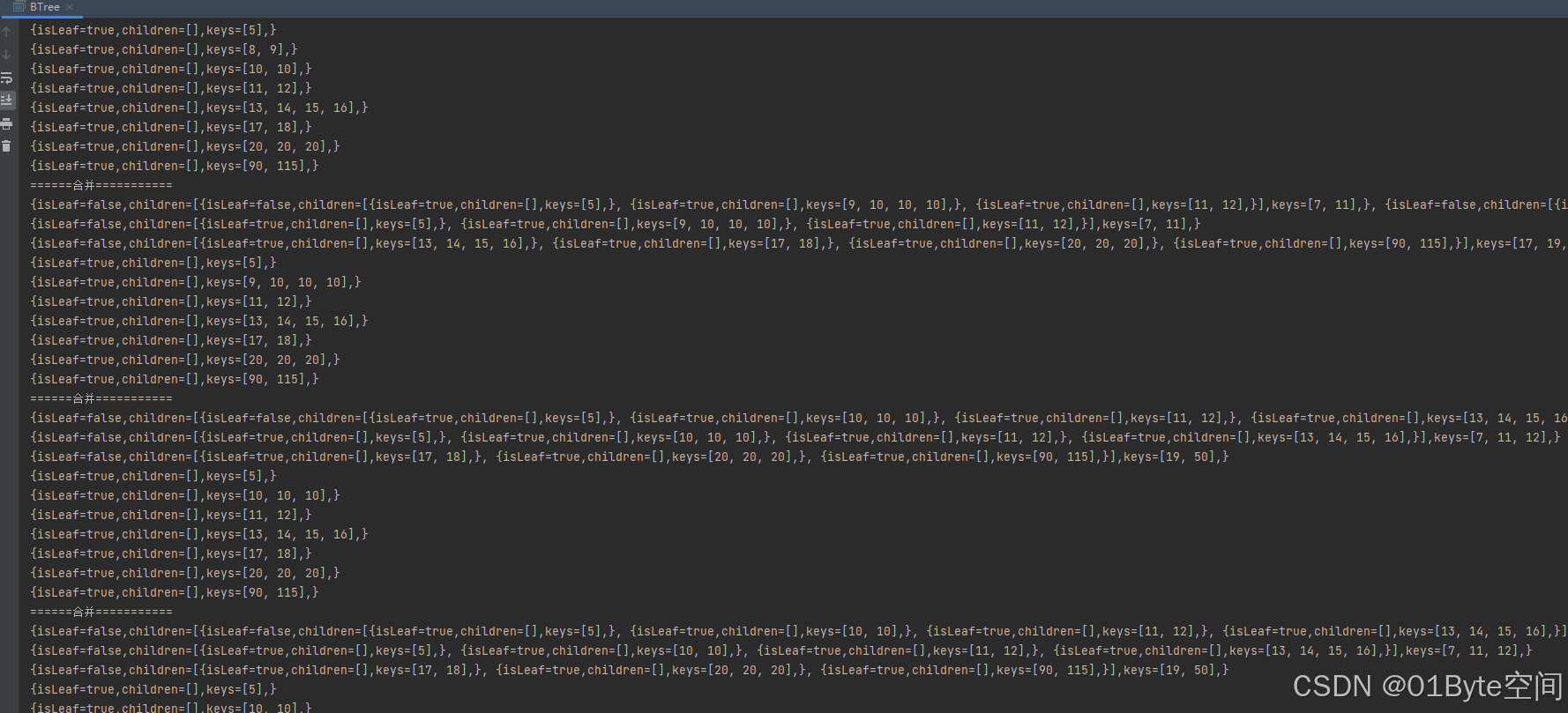
            btree.levelOrderTraversal();//打印可以看到分裂和合并
            System.out.println("=================" );
        }
        System.out.println("\n=================\n" );
        // 测试搜索操作
        System.out.println("搜索 6: " + (btree.search(6) != null)); // 应该存在
        System.out.println("搜索 15: " + (btree.search(15) != null)); // 应该不存在

        // 测试删除操作
        int[] deleteKeys = {6, 15, 30};
        for (int key : deleteKeys) {
            btree.delete(key);
        }

        // 再次测试搜索操作
        System.out.println("搜索 6: " + (btree.search(6) != null)); // 应该不存在
        System.out.println("搜索 30: " + (btree.search(30) != null)); // 应该不存在

        // 测试节点分裂和合并
        for (int i = 1; i <= 20; i++) {
            btree.insert(i);
            btree.levelOrderTraversal();//打印可以看到分裂和合并
            System.out.println("=======分裂==========" );
        }
        System.out.println("\n=================\n" );
        for (int i = 1; i <= 10; i++) {
            btree.delete(i);
            btree.levelOrderTraversal();//打印可以看到分裂和合并
            System.out.println("======合并===========" );
        }
    }
}

/**
 * 经过检查，上述Java代码实现的B树基本功能（插入、删除、搜索、节点分裂和合并）在逻辑上是正确的，但有一些细节需要注意和改进：
 *
 * 注意事项：
 * 1. 边界条件处理：在删除操作中，处理边界条件时需要特别小心，确保不会出现数组越界等问题。
 * 2. 代码优化：可以进一步优化代码结构和性能，例如在插入和删除操作中减少不必要的列表复制和查找。
 *
 * 测试用例：为了验证B树的正确性，可以设计以下测试用例：
 *
 * 测试用例1：插入操作
 * 1. 插入关键字序列：10, 20, 5, 6, 12, 30, 7, 17
 * 2. 验证B树的结构和关键字顺序是否正确。
 *
 * 测试用例2：搜索操作
 * 1. 在上述插入操作后的B树中，搜索关键字：6, 15, 30
 * 2. 验证搜索结果是否正确（6 和 30 应该存在，15 应该不存在）。
 *
 * 测试用例3：删除操作
 * 1. 在上述插入操作后的B树中，删除关键字序列：6, 15, 30
 * 2. 验证B树的结构和关键字顺序是否正确。
 *
 * 测试用例4：节点分裂和合并
 * 1. 插入足够多的关键字，使得B树的根节点需要分裂。
 * 2. 删除足够多的关键字，使得B树的某个节点需要合并。
 * 3. 验证B树的结构和关键字顺序是否正确。
 *
 * 测试用例5：边界条件
 * 1. 插入和删除最小和最大关键字。
 * 2. 插入和删除重复关键字（B树通常不允许重复关键字，需要根据具体实现验证）。
 * */

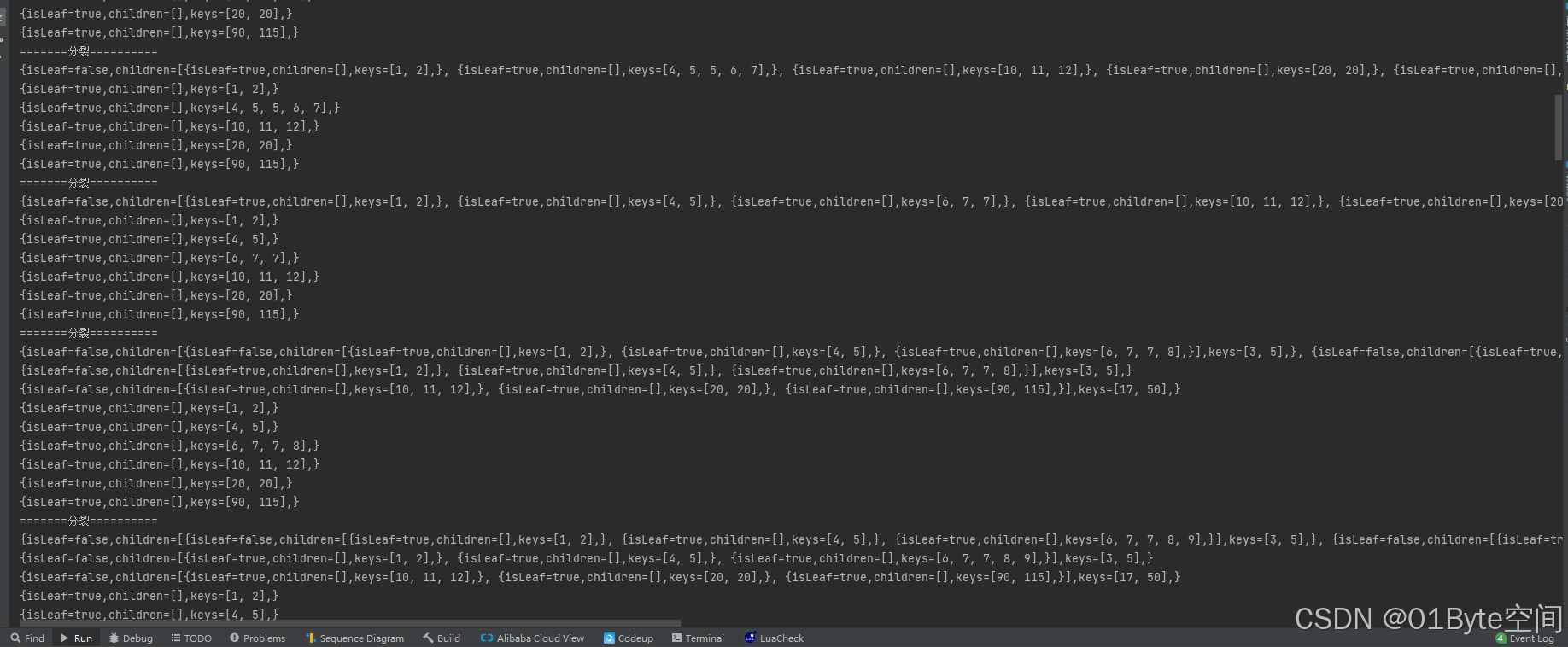
观察分裂合并过程