目录
Python 简介
Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。
Python 的设计具有很强的可读性,相比其他语言经常使用英文关键字,其他语言的一些标点符号,它具有比其他语言更有特色语法结构。
-
Python 是一种解释型语言: 这意味着开发过程中没有了编译这个环节。类似于PHP和Perl语言。
-
Python 是交互式语言: 这意味着,您可以在一个 Python 提示符 >>> 后直接执行代码。
-
Python 是面向对象语言: 这意味着Python支持面向对象的风格或代码封装在对象的编程技术。
-
Python 是初学者的语言:Python 对初级程序员而言,是一种伟大的语言,它支持广泛的应用程序开发,从简单的文字处理到 WWW 浏览器再到游戏。
Python 特点
-
1.易于学习:Python有相对较少的关键字,结构简单,和一个明确定义的语法,学习起来更加简单。
-
2.易于阅读:Python代码定义的更清晰。
-
3.易于维护:Python的成功在于它的源代码是相当容易维护的。
-
4.一个广泛的标准库:Python的最大的优势之一是丰富的库,跨平台的,在UNIX,Windows和Macintosh兼容很好。
-
5.互动模式:互动模式的支持,您可以从终端输入执行代码并获得结果的语言,互动的测试和调试代码片断。
-
6.可移植:基于其开放源代码的特性,Python已经被移植(也就是使其工作)到许多平台。
-
7.可扩展:如果你需要一段运行很快的关键代码,或者是想要编写一些不愿开放的算法,你可以使用C或C++完成那部分程序,然后从你的Python程序中调用。
-
8.数据库:Python提供所有主要的商业数据库的接口。
-
9.GUI编程:Python支持GUI可以创建和移植到许多系统调用。
-
10.可嵌入: 你可以将Python嵌入到C/C++程序,让你的程序的用户获得"脚本化"的能力。
认识数据分析
数据分析是大数据技术的重要组成部分。近年来,随着大数据技术的逐渐发展,数据分析技能被认为是数据科学领域中数据从业人员需要具备的技能之一。与此同时,数据分析师也成了时下最热门的职业之一.掌握数据分析技能是一个循序渐进的过程,明确数据分析概念、流程和应用场景等相关知识是掌握数据分析的第一步。
Jupyter Notebook(此前被称为 IPython Notebook)是一个交互式笔记本,支持运行 40 多种编程语言,本质上是一个支持实时代码、数学方程可视化和 Markdow 的 Web 应用程序。对于数据分析,Jupyter Notebook的优点是可以重现整个分析过程,并将说明文字、代码、图表、公式和结论都整合在一个文档中。用户可以通过电子邮件、Dropbox、GitHub 和Jupyter Notebook Viewer 将分析结果分享给其他人。
一、如何进入jupyter notebook
先找到这个
点击打开它
输入完jupyter notebook 然后回车就可以进去了

在这里新建文件
点击这里可以改文件名

二、下面我们进行数据清洗
1.方法一
import pandas as pd
download = pd.read_csv('E:/21rgznjsyy1b/py数据分析/新建文件夹/user_download.csv',index_col=0,encoding='gbk',engine='python')
#方法一
#定义去重函数
def del_rep(list1): # 定义一个函数del_rep,接受一个列表参数list1
list2 = [] # 定义一个空列表list2,用于存储去重后的新列表
for i in list1: # 遍历列表list1中的每一个元素
if i not in list2: # 如果这个元素不在新列表list2中
list2.append(i) # 将这个元素添加到新列表list2中
return list2 #返回新列表list2
#这个函数的实现方法是遍历原列表,将不在新列表中的元素添加到新列表中,从而实现去重的效果。
#去重
#将下载意愿从数据框中提取出来
download = list(download['是否愿意下载'])
print('去重前下载意愿选项总数为:',len(download))
download_rep = del_rep(download) # 使用自定义的去重函数去重
print('方法一去重后下载意愿选项总数为: ',len(download_rep))
print('用户选项为:',download_rep)
运行结果
去重前下载意愿选项总数为: 2175 方法一去重后下载意愿选项总数为: 1 用户选项为: ['Yes']
2.方法二
#代码4-8
#方法二E:/python_r/user_download.csv
print('去重前下载意愿选项总数为:',len(download))
download_set = set(download)#利用set的特性去重
print('方法二去重后下载意愿选项总数:',len(download_set))
print('用户选项为:',download_set)
运行结果
去重前下载意愿选项总数为: 2175
方法二去重后下载意愿选项总数: 3
用户选项为: {nan, 'Yes', 'No'}
3.接下来我们对下载意愿去重
download =pd.read_csv('E:/21rgznjsyy1b/py数据分析/新建文件夹/user_download.csv',encoding='gbk',engine='python')
download_select = download['是否愿意下载'].drop_duplicates()
print('drop_duplicates方法去重后下载意愿选项总数为:',len(download_select))运行结果
drop_duplicates方法去重后下载意愿选项总数为: 3
all_info = pd.read_csv('E:/21rgznjsyy1b/py数据分析/新建文件夹/user_all_info.csv',engine='python',encoding='utf-8')
print('去重之前用户的形状为:',all_info.shape)
shape_det = all_info.drop_duplicates(subset = ['用户编号','编号']).shape
print('依照用户编号,编号去重之后用户总信息表大小为:',shape_det)
运行结果
去重之前用户的形状为: (2235, 7) 依照用户编号,编号去重之后用户总信息表大小为: (2172, 7)
4.求取年龄和每月支出的相似度
corr_det =all_info[['年龄','每月支出']].corr(method='kendall')
print('年龄和每月支出的相似度矩阵为:\n',corr_det)运行结果
年龄和每月支出的相似度矩阵为:
年龄 每月支出
年龄 1.000000 0.011119
每月支出 0.011119 1.000000
corr_det1 = all_info[['居住类型','年龄','每月支出']].corr(method='pearson')
print('居住类型、年龄和每月支出的pearson法相似度矩阵为:\n',corr_det1)运行结果
居住类型、年龄和每月支出的pearson法相似度矩阵为:
年龄 每月支出
年龄 1.000000 0.014168
每月支出 0.014168 1.000000
实训
实训1 分析学生考试成绩特征的分布与分散情况
1.训练要点
(1)掌握 pyplot 的基础语法。
(2)掌握饼图的绘制方法。
(3)掌握箱线图的绘制方法。
2.需求说明
在期末考试后,学校对学生的期末考试成绩及其他特征信息进行了统计,并存为学生绩特征关系表(student grade.xlsx)。学生成绩特征关系表共有 7个特征,分别为性别、自我效能感、考试课程准备情况、数学成绩、阅读成绩、写作成绩和总成绩,其部分数据如表541所示。为了解学生考试总成绩的分布情况,将总成绩按 0~150、150~200、200~250、250300区间划分为“不及格”“及格”“良好”“优秀”4 个等级,通过绘制饼图查看各区间学生人数比例,并通过绘制箱线图查看学生 3 项单科成绩的分散情况
3.实现步骤
(1)使用 pandas 库读取学生考试成绩数据。
(2)将学生考试总成绩分为 4 个区间,计算各区间下的学生人数,绘制学生考试总成绩分布饼图。
(3)提取学生3 项单科成绩的数据,绘制学生各项考试成绩分散情况箱线图。
(4)分析学生考试总成绩的分布情况和3 项单科成绩的分散情况。
先导入库
import numpy as np
import matplotlib.pyplot as plt
读取数据
plt.rcParams['font.sans-serif'] = 'SimHei'#设置中文
plt.rcParams['axes.unicode_minus'] = False
data = np.load('E:/21rgznjsyy1b/py数据分析/新建文件夹/student_grade.npz', encoding='ASCII',allow_pickle=True)
columns = data['arr_0']
values = data['arr_1']
#columns包合数据的列名,values是包含数据的二维数组
# 声定义成绩变量
math_grade = values[:,-4]
reading_grade = values[:,-3]
writing_grade = values[:,-2]
all_grade = values[:, -1]
student_id = np.arange(len(values))
p =plt.figure(figsize=(15,15))
#将每个学生的数学、阅读、写作、总成绩以及学生ID分别存储在相应的变量中
# 提取学生考试总成绩区间人数
grade_0_150 = 0
grade_150_200 = 0
grade_200_250 = 0
grade_250_300 = 0
for i in range(len(values)):
if 0 < values[i,-1] <= 150:
grade_0_150 += 1
elif 150 < values[i,-1] <= 200:
grade_150_200 +=1
elif 200 < values[i, -1] <= 250:
grade_200_250 += 1
elif 250 < values[i,-1] <= 300:
grade_250_300 += 1
all_stu_grade = [grade_0_150, grade_150_200, grade_200_250, grade_250_300]
#使用for循环遍历每个学生的总成绩,根据总成绩的范围,参加人数。最终将每个区间的人数存储在一个列表中
#绘制学生考试总成绩分布情况饼图
p =plt.figure(figsize=(12,12))# 设置画布
label=['不及格','及格','良好','优秀']
explode =[0.01,0.01,0.01,0.01] #没定客晚离心n个半检
plt.pie(all_stu_grade,explode=explode, labels=label,
autopct='%1.1f%%', textprops={'fontsize': 15})
plt.title('学生考试总成绩的总体分布情况饼图',fontsize=20)
plt.savefig('E:/21rgznjsyy1b/py数据分析/学生考试总成绩的总体分布情况饼图.png')
plt.show()
#绘制学生考试总成绩的总体分布停况饼图,设置标签、离心半径、标签字体大小和标题,最后保存图片并显示
#绘制学生考试总成绩的点体分教信况箱线图
p = plt.figure(figsize=(16,8))
label=['数学成绩','阅读成绩','写作成绩']
gdp = (list(math_grade), list(reading_grade),list(writing_grade))
plt.boxplot(gdp,notch=True,labels=label,meanline=True) #绘制箱线图
plt.xlabel('学生考试科目')
plt.ylabel('学生考试分数')
plt.title('学生各项考试成绩的总体分散情况箱线图',fontsize=20)
plt.savefig('E:/21rgznjsyy1b/py数据分析/新建文件夹/学生考试总成绩的总体分布情况箱线图.png')
plt.show()
输出结果:


实训2 分析学生考试成绩与各个特征之间的关系
1.训练要点
(1) 掌握子图的绘制方法。
(2) 掌握柱形图的绘制方法。
(3)掌握 NumPy 库中相关函数的使用方法。
2.需求说明
为了了解学生自我效能感、考试课程准备情况这两个特征与总成绩之间是否存在某些关系,基于实训1的数据,对这两个特征下不同值所对应的学生总成绩求均值,绘制柱形图分别查看自我效能感、考试课程准备情况与总成绩的关系,并对结果进行分析。
3.实现步骤
(1)创建画布,并添加子图。
(2)使用 NumPy 库中的均值函数求学生自我效能感、考试课程准备情况两个特征下对应学生总成绩的均值。
(3)在子图上绘制对应内容的柱形图。
(4)分析两个特征与考试总成绩的关系。
plt.rcParams['font.sans-serif'] = 'SimHei'#设置中文
plt.rcParams['axes.unicode_minus'] = False
student_grade = pd.read_excel('E:/21rgznjsyy1b/py数据分析/新建文件夹/student_grade.xlsx')
#分别提取自我效能感对应的总成绩,并计草平均值
high = np.mean(student_grade.iloc[(student_grade['自我效能感']=='高').values,-1])
middle = np.mean(student_grade.iloc[(student_grade['自我效能感']=='中').values,-1])
low = np.mean(student_grade.iloc[(student_grade['自我效能感']=='低').values,-1])
mean_self_efficacy = [round(high),round(middle),round(low)]
#分别提取考试课程准备情况对应的总complete成绩,并计意平均值
complete = np.mean(student_grade.iloc[(student_grade['考试课程准备情况']=='未完成').values,-1])
incomplete = np.mean(student_grade.iloc[(student_grade['考试课程准备情况']=='完成').values,-1])
mean_situation = [round(complete),round(incomplete)]
p = plt.figure(figsize=(15,8)) #设置画布
# 子图1
ax2 = p.add_subplot(1,2,1)
label = ['高','中','低']
plt.bar(range(3),mean_self_efficacy,width=0.4) #绘制柱形图
plt.xlabel('自我效能感')
plt.ylabel('学生平均考试总成绩')
plt.xticks(range(3),label)
plt.title('学生平均考试总成绩与自我效能感关系柱形图')
# 子图2
ax2 = p.add_subplot(1,2,2)
label = ['已完成','未完成']
plt.bar(range(2),mean_situation,width=0.4) #绘制柱形图
plt.xlabel('考试课程准备情况')
plt.ylabel('学生平均考试总成绩')
plt.xticks(range(2),label)
plt.title('学生平均考试总成绩与考试课程准备情况关系柱形图')
plt.savefig('E:/21rgznjsyy1b/py数据分析/新建文件夹/学生考试总成绩与各个特征关系图.png')输出结果:

我们画一个特征矩阵热力图来试试看
boston=pd.read_csv('E:/21rgznjsyy1b/py数据分析/新建文件夹/boston_house_prices.csv',encoding='gbk')
plt.rcParams['axes.unicode_minus']=False
corr=boston.corr() #特征的相关系数矩阵
sns.heatmap(corr) #,vmin=0.0,vmax=100.0,center=1.0,robust=True,annot=True,fmt=.2f,linewidths=5,linecolor=black,square=True
plt.title('特征矩阵热力图')
plt.show()输出结果:

plt.figure(figsize=(10,10))
sns.heatmap(corr,annot=True,fmt='.2f')
plt.title('特征矩阵热力图')
plt.show()输出结果 :

绘制3D散点图试试看
# 最大携氧能力、体重和运动后心率的三维散点图
import pandas as pd
import numpy as np
from pyecharts import options as opts
from pyecharts.charts import Scatter3D
player_data = pd.read_excel('E:/21rgznjsyy1b/py数据分析/新建文件夹/运动员的最大携氧能力、体重和运动后心率数据.xlsx')
player_data = [player_data['体重(kg)'], player_data['运动后心率(次/分钟)'],
player_data['最大携氧能力(ml/min)']]
player_data = np.array(player_data).T.tolist()
s = (Scatter3D()
.add('', player_data, xaxis3d_opts=opts.Axis3DOpts(name='体重(kg)'),
yaxis3d_opts=opts.Axis3DOpts(name='运动后心率(次/分钟)'),
zaxis3d_opts=opts.Axis3DOpts(name='最大携氧能力(ml/min)')
)
.set_global_opts(title_opts=opts.TitleOpts(
title='最大携氧能力、体重和运动后心率3D散点图'),
visualmap_opts=opts.VisualMapOpts(range_color=[
'#1710c0', '#0b9df0', '#00fea8', '#00ff0d', '#f5f811', '#f09a09',
'#fe0300'])))
s.render_notebook()
输出结果 :

我们绘制漏斗图试试看
from pyecharts.charts import Funnel
data = pd.read_excel('E:/21rgznjsyy1b/py数据分析/新建文件夹/某淘宝店铺的订单转化率统计数据.xlsx')
x_data = data['网购环节'].tolist()
y_data = data['人数'].tolist()
data = [[x_data[i], y_data[i]] for i in range(len(x_data))]
funnel = (Funnel()
.add('', data_pair=data,label_opts=opts. LabelOpts(
position='inside', formatter='{b}:{d}%'), gap=2,
tooltip_opts=opts.TooltipOpts(trigger='item'),
itemstyle_opts=opts.ItemStyleOpts(border_color='#fff', border_width=1))
.set_global_opts(title_opts=opts.TitleOpts(title='某淘宝店铺的订单转化率漏斗图'),
legend_opts=opts.LegendOpts(pos_left='40%')))
funnel.render_notebook()输出结果:
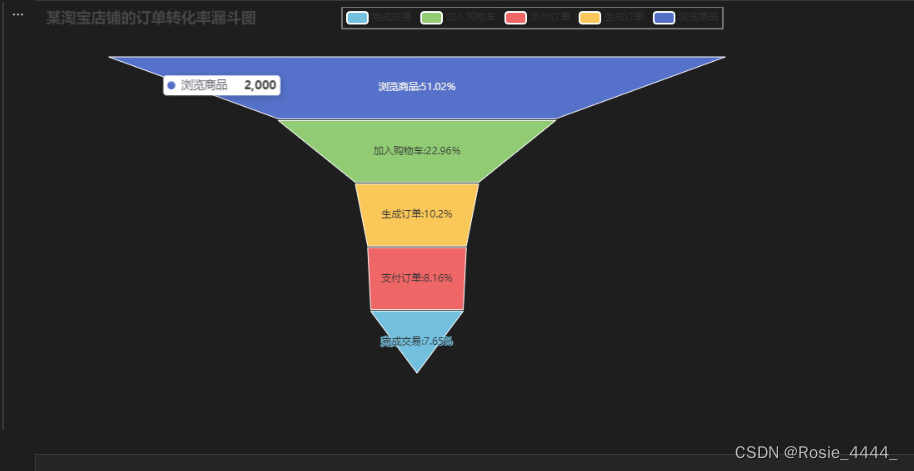







 本文介绍了Python在数据分析中的应用,特别是通过JupyterNotebook进行数据清洗,包括去重方法对比。此外,还展示了如何使用Python绘制饼图、箱线图、特征矩阵热力图、3D散点图和漏斗图,以分析学生考试成绩和其它特征。这些工具和方法对于理解和探索数据集非常有用。
本文介绍了Python在数据分析中的应用,特别是通过JupyterNotebook进行数据清洗,包括去重方法对比。此外,还展示了如何使用Python绘制饼图、箱线图、特征矩阵热力图、3D散点图和漏斗图,以分析学生考试成绩和其它特征。这些工具和方法对于理解和探索数据集非常有用。
















 2195
2195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








